
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Производная и её приложение
|
|
141-150. Найти производные 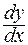 данных функций.
данных функций.
141. а)  ; б)
; б) 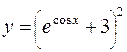 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
142. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 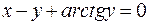 .
.
143. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  .
.
144. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
145. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 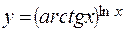 ; д)
; д)  .
.
146. а) 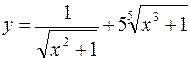 ; б)
; б) 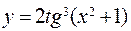 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
147. а) 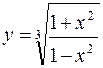 ; б)
; б) 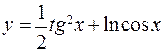 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
148. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д) 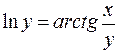 .
.
149. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 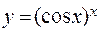 ; д)
; д)  .
.
150. а) 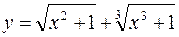 ; б)
; б)  ;
;
в)  ; г)
; г) 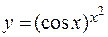 ; д)
; д)  .
.
151-160. Найти 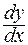 и
и 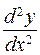 .
.
151. а)  ; б)
; б)  .
.
152. а)  ; б)
; б)  .
.
153. а)  ; б)
; б) 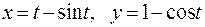 .
.
154. а)  ; б)
; б)  .
.
155. а)  ; б)
; б)  .
.
156. а) 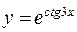 ; б)
; б)  .
.
157. а)  ; б)
; б)  .
.
158. а)  ; б)
; б) 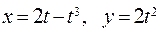 .
.
159. а)  ; б)
; б) 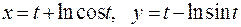 .
.
160. а)  ; б)
; б)  .
.
Приложения дифференциального исчисления
191-200. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191.  . 192.
. 192.  .
.
193.  . 194.
. 194. 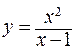 .
.
195. 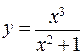 . 196.
. 196.  .
.
197.  . 198.
. 198. 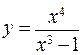 .
.
199.  . 200.
. 200.  .
.
Неопределённый и определённый интегралы
281-290. Найти неопределенные интегралы. В двух примерах (пункты а и б) проверить результаты дифференцированием.
281. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 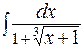 .
.
282. а) 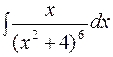 ; б)
; б) 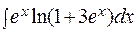 ;
;
в)  ; г)
; г)  .
.
283. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
284. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
285. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 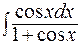 .
.
286. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 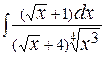 .
.
287. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
288. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
289. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
290. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 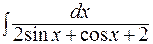 .
.
301-310. Вычислить несобственный интеграл или доказать его расходимость.
30 1.  . 30 2.
. 30 2. 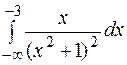 . 30 3.
. 30 3.  . 30 4.
. 30 4.  . 30 5.
. 30 5.  . 306.
. 306.  .
.
30 7.  . 30 8.
. 30 8.  . 30 9.
. 30 9. 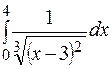 . 310.
. 310.  .
.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЙ
Задание 11 – 20
Для решения задач 11 – 20 рекомендуется учебное пособие
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.
Ч.1. М.: Оникс 21 век. 2005. Гл. I –IV, стр.39 – 91.
Рассмотрим решение аналогичной задачи, взяв координаты вершины пирамиды SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).
1) Длину ребра АВ находим по формуле:

2) Угол между рёбрами  найдём по формуле косинуса угла между векторами
найдём по формуле косинуса угла между векторами 
 , координаты которых определяются так:
, координаты которых определяются так:






α
φ
Для решения задания 3) целесообразно решить задачу 7). Уравнение плоскости  составим по уравнению
составим по уравнению
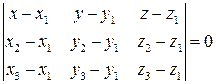


Нормальный вектор этой плоскости

4) Площадь  определяем с помощью векторного произведения:
определяем с помощью векторного произведения:


5) Объём пирамиды  находится через вычисление смешанного произведения векторов
находится через вычисление смешанного произведения векторов  Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.
Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. Решите самостоятельно.
6) Уравнение прямой 


Канонические уравнения прямой, вектор  направляющий вектор прямой
направляющий вектор прямой 
8) Для определения проекции вершины  на плоскость
на плоскость  выполняются следующие действия:
выполняются следующие действия:
а) составляется уравнение высоты пирамиды  .
.
б) находится точка пересечения высоты и основания  решением системы, содержащей уравнение высоты и уравнение плоскости.
решением системы, содержащей уравнение высоты и уравнение плоскости.
Решение: вектор  удобнее взять
удобнее взять 

Он будет направляющим для  По уравнению
По уравнению 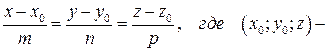
вершина  , т.е.
, т.е. 
 .
.
Система  решается подстановкой
решается подстановкой

Подставив во второе уравнение, найдём значение  , а следовательно значения
, а следовательно значения


Точка  - проекция точки
- проекция точки  на плоскость
на плоскость 
9) Длину высоты  пирамиды можно найти по формуле
пирамиды можно найти по формуле  или по формуле расстояния от точки до плоскости – наиболее удобно.
или по формуле расстояния от точки до плоскости – наиболее удобно.
Изучите формулы самостоятельно, решив задание 9).
Задание 51 – 60
Дана система линейных уравнений

Решить систему а) матричным методом, б) методом Крамера, в) методом Гаусса.
а) данной системе соответствует матричное уравнение  , которое решается по формуле:
, которое решается по формуле:  . Матрицы имеют вид:
. Матрицы имеют вид:

Находим обратную матрицу


Находим матрицу 

б)  - формулы Крамера. Вычислим все определители
- формулы Крамера. Вычислим все определители 

в) Метод Гаусса.
Составим расширенную матрицу 
 и преобразуем её с помощью элементарных преобразований.
и преобразуем её с помощью элементарных преобразований.

Из полученной матрицы, выделяя последнюю строку, видим, что исключены неизвестные  и
и 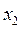 . Найдём
. Найдём  .
.  .
.
Вторая строка соответствует уравнению:
 или
или 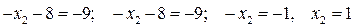
Аналогично из первой строки напишем уравнение:

Итак: 
Задание 91 – 100.
Дано комплексное число 
Записать число  в геометрической и тригонометрической формах и найти все корни уравнения
в геометрической и тригонометрической формах и найти все корни уравнения 
Рекомендуемая литература: Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. II, гл.III, §7, стр.97 – 101.
Найдём алгебраическую форму комплексного числа

Тригонометрическая форма комплексного числа  определится по формуле
определится по формуле  .
.
Изобразив число на плоскости, найдём  и
и  .
. 





 -1
-1 



Итак, число 
Найдём корни уравнения 
 вычислим по формуле Муавра
вычислим по формуле Муавра




Задание 111 – 120
Вычислить пределы:
а) 
За скобку выносили наивысшую степень  для числителя и знаменателя.
для числителя и знаменателя.
б) 
Для исключения неопределённости  требуется числитель и знаменатель разложить на множители.
требуется числитель и знаменатель разложить на множители.
в) 

В данном случае для исключения неопределённости  использованы эквивалентные бесконечно малые, например
использованы эквивалентные бесконечно малые, например 
 г) Числитель и знаменатель умножаем на выражение, сопряжённое числителю
г) Числитель и знаменатель умножаем на выражение, сопряжённое числителю

Задание 141– 150
Найти производные  следующих функций:
следующих функций:
а)  б)
б)  ;
;
в)  г)
г)  ;
;
д)  .
.

б) 
в) 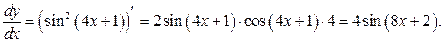
г) 
Прологарифмируем обе части равенства

Продифференцируем обе части равенства




д) 
Функция  задана неявно. Учитываем, что
задана неявно. Учитываем, что  аргумент,
аргумент,  функция.
функция.

Задание 151 – 160
Найти  функций:
функций:

Решение:
а) 

б) 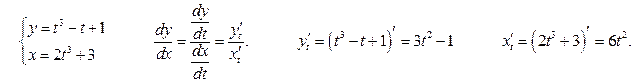

Задание 191 – 200
Исследовать методами дифференциального исчисления функцию и построить её график.

Рассмотрим свойства функции:
1. Область определения: 
2. Чётностьь, нечётность функции: 
Функция общего вида.
3. Асимптоты.
а) Так как  , то прямая
, то прямая  является вертикальной асимптотой:
является вертикальной асимптотой:

б)  – наклонная асимптота.
– наклонная асимптота.
Найдём 
Найдём 
 – уравнение наклонной асимптоты.
– уравнение наклонной асимптоты.
4. Найдём точки экстремума и интервалы монотонности функции:


Так как  то действительных корней нет, значит, нет точек экстремума.
то действительных корней нет, значит, нет точек экстремума.
Производная  на всей области определения, значит функция
на всей области определения, значит функция
 убывает.
убывает.
5. Точки пересечения с координатными осями
а) с осью  при
при 
 ,
,
б) с осью  при
при 
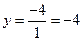 .
.
Используя исследование функции, строим график (схематично).

 Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.
Задания 141-150, 151-160, 191-200 легко выполнить, используя учебное пособие П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах ч.I гл. VII §§ 1-2 стр. 151-183.

Задание 281 – 290
Найти неопределённые интегралы, выполнив проверку дифференцированием в первых двух примерах.

Решение:

Проверка:


Метод интегрирования по частям для функции 
Формула: 
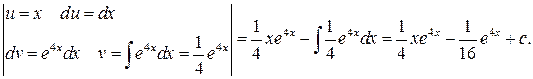
Проверка:


Найдём коэффициенты






.
Литература
Основная литература
1.Фихтенгольц Г.М. Основы математического анализа [Электронный ресурс]: учебник для вузов. Ч.1/ Г.М. Фихтенгольц. – 10-е изд., стер. – Электрон. текстовые дан. – Санкт-Петербург; Москва; Краснодар: Лань, 2015. – 440 с.
2. Справочник по математике для бакалавров [Электронный ресурс]: учебное пособие для вузов / [А. Ю. Вдовин и др.]. – Электрон. текстовые дан. – Санкт-Петербург; Москва; Краснодар: Лань, 2014. – 79 с.
3. Высшая математика для экономических специальностей [Текст]: учебник и практикум для вузов/ Н.Ш. Кремер и др.; под ред. Н.Ш. Кремера. – 3-е изд., перераб. и доп. Москва: Юрайт, 2011. – 909 с.
4. Туганбаев А.А. Задачи и упражнения по высшей математике для гуманитариев [Электронный ресурс]: учебное пособие для вузов / А. А. Туганбаев. – 4-е изд., испр. и доп. – Электрон. текстовые дан. – Москва: Флинта, 2011. – 399 с.
Дополнительная литература:
5. Пискунов Н.С. Дифференциальное и интегральное исчисления [Текст] / Н.С. Пискунов. В 2-х т. – М.: Интеграл-Пресс, 2005.
6. Шолохович Ф.А., Васин В.В. Основы высшей математики. [Текст] /
Ф.А. Шолохович, В.В. Васин. – Екатеринбург, Изд-во УрГУ, 2004.
7. Шипачев В.С. Основы высшей математики. [Текст] / В.С. Шипачев. – М.: Высшая школа, 2004.
8. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика в упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. В 2 ч. – М.: Высшая школа, 2007.
9. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики. [Текст] / Б.П. Демидович, В.А. Кудрявцев. – М.: ООО "Изд. Астрель", 2001
ЗАДАНИЯ и методические указания к выполнению
Date: 2016-11-17; view: 331; Нарушение авторских прав