Определение: Функция ,имеющая конечную производную в точке х0 называется дифференцируемойв этой точке ,а процесс нахождения ее производной называется дифференцированием.

Вопрос 14.

Понятие производной в точке.

Определение: Пусть функция y=f(x) определяется на Х,х0∈Х, х∈Х, ΔХ=х-х0, следовательно х=х0+Δх; y=f(x)=(x0+Δx); Δy=y-y0=f(x)-f(x0).

Тогда производной функцией y=f(x) в точке x0 называется:

Если предел в равенстве не существует,то функция y=f(x) не имеет производной в точке х0.

Определение: Функция,имеющая конечную производную в точке х0 называется дифференцируемойв этой точке,а процесс нахождения ее производной называется дифференцированием.

Односторонние производные.

Определение: Правой производной функции y=f(x) в точке х0 называется:

Определение: Левой производной функции y=f(x) в точке х0 называется:

Утверждение:

Геометрический смысл производных.

Теорема(ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ): если функция дифференцируема в точке х0,то график у=f(x) имеет в точке (х0,f(x0)) касательную с условным коэффицентом f' (x0).

Утверждение: y=y0+f' (x0)(x-x0),где y0=f(x0)- уравнение касательной к функции y=f(x) в точке х0.

Замечание: Если f' (x0)=0,то касательная в этой точке горизонтальная.

Если f' (x0)= ∞,то касательная в этой точке вертикальная.

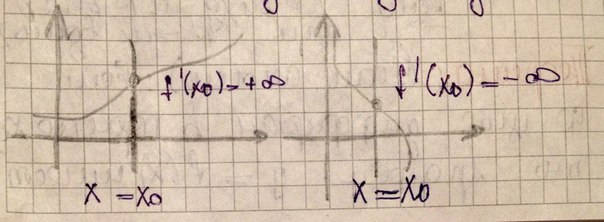
Замечание: Если y=f(x) непрерывна в точке х0 и f' (x0)= ∞,то в окрестности этой точки график функции имеет один из видов:

Date: 2016-11-17; view: 356; Нарушение авторских прав