
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

де функциясының ең үлкен мәнін табыңыздар. A) 160 B)320/2 G)480/3
|
|
 +y+z-2=0 жазықтығы: E)кординаталық өстерден 2-ге тең кесінділер қиядыG)Ox өсінен 2-ге тең кесінді қияды
+y+z-2=0 жазықтығы: E)кординаталық өстерден 2-ге тең кесінділер қиядыG)Ox өсінен 2-ге тең кесінді қияды
22M(1;-2)нүктесінде 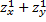 -нің мәні,егер
-нің мәні,егер  : A)
: A)  D)
D) 
2х+y-7=0 түзуінде жатқан нүкте: C)(1;5)E)(0;7)
2х+у-7 =0 түзуінде жатқан нүкте: А) (1; 5)В) (0; 7);(-1;9)
2х+у-7=0 түзуінде жатқан нүкте: А)  В)
В) 
3  векторының ұзындығы тең: B)
векторының ұзындығы тең: B)  D)2E)
D)2E) 
3х-у+2z-3=0 гиперболоиды: C)оz өсі бойымен созылғанG)Бірдей жарты өстермен
5 Х + 3 кездейсоқ шаманың математикалық үмітін табыңыз. A)68 D)  G)
G) 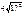
A(2,2)жәнеВ(5,-2)нүктелері берілген.  кесіндісінің ортасының абциссасы: 3,5; теріс емес сан
кесіндісінің ортасының абциссасы: 3,5; теріс емес сан
A(2,2) және B(5,-2) нүктелері берілген.  кесіндісінің ортасының ординатасы: A) теріс емес санB) бүтін санC) 0
кесіндісінің ортасының ординатасы: A) теріс емес санB) бүтін санC) 0
A(2,2)жәнеВ(5,-2)нүктелері берілген.  векторының ординатасы: E)оң сан
векторының ординатасы: E)оң сан
A(4,6)жәнеB(-1,-4)нүктелері арқылы өтетін түзудің бұрыштық коэффициентін табу керек: B)2D)  E)
E) 
 A) 6 D)
A) 6 D)  G)
G) 
 A)Бүтін сан
A)Бүтін сан
 шегі: 0-ден кіші; -1-ден үлкен
шегі: 0-ден кіші; -1-ден үлкен
 ; А) оң сан
; А) оң сан
 шегі: 10-нан кіші; 8-ден үлкен
шегі: 10-нан кіші; 8-ден үлкен
 : нақты сан;оң сан; 3/2
: нақты сан;оң сан; 3/2
 шегі: 3-тен кіші; 2-ге тең; 1-ден үлкен
шегі: 3-тен кіші; 2-ге тең; 1-ден үлкен
 шегі: 0-ден үлкен; е-2-не тең
шегі: 0-ден үлкен; е-2-не тең
 шегі: е-ден үлкен; е2-не тең; е3-нен кіші
шегі: е-ден үлкен; е2-не тең; е3-нен кіші
 шегінің мәні жататын аралық: [-1; 1], [0; 2]
шегінің мәні жататын аралық: [-1; 1], [0; 2]
C  ,D
,D  .C-D матрицасын табу керек: B)
.C-D матрицасын табу керек: B) 
x+y+z-2=0 жазықтығы: В) координаталық өстерден 2-ге тең кесінділер қиядыЖ) Ох өсінен 2-ге тең кесінді қияды
x2+y2=9 шеңберінің радиусын анықтаңыз: А) 3 В)  С) 9/3
С) 9/3
x2+y2=9 шеңберінің радиусын анықтаңыз: C) 3 D)  G) 9/3
G) 9/3
Z=5х2-3у2х+8у-2 функциясы берілген. А(1;1) нүктесіндегі  -нің мәні: A)2B)
-нің мәні: A)2B)  G)21
G)21
Z=5х2-4у2х+8у-3 функциясы берілген. А(2;1) нүктесіндегі  -нің мәні: A)-8; E)-23
-нің мәні: A)-8; E)-23
А(-1;3) және В(2;3) нүктелері арқылы өтетін түзудің теңдеуі: А) у-3=0;y=3;  ;
;
А(1;2) және В(-3;2) нүктелері арқылы өтетін түзудің теңдеуі: у-2=0; у=2; 
А(2,2) және В (5,-2) нүктелері берілген.  кесіндісінің ортасының абциссасы: А) оң санВ) теріс емес сан; 3,5
кесіндісінің ортасының абциссасы: А) оң санВ) теріс емес сан; 3,5
А(-3,1), В(0,5) нүктелері берілген.  векторының координаталары тең: А) (-3;-4) D) (-9/3;-16/4) G) (-27/9;-12/3)
векторының координаталары тең: А) (-3;-4) D) (-9/3;-16/4) G) (-27/9;-12/3)
А(3,3,5) және В(2,1,3) нүктелерінің арақашықтығын табу керек: C)  F)
F) 
А(3,3,5) және В(2,1,3) нүктелерінің арақашықтығын табыңыздар. C)3 E)  H)9/3
H)9/3
А(4,6) және В(–1,-4) нүктелері арқылы өтетін түзудің бұрыштық коэффициентін табыңдар. A)2 B)  C)
C) 
 А)
А) 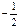 :А) 0,2
:А) 0,2
 А) 1
А) 1
 А) 1/15 В) рационал сан С) оң сан
А) 1/15 В) рационал сан С) оң сан
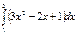 А) 5 / В) бүтін сан
А) 5 / В) бүтін сан
 А) оң санС) бүтін санД) 5
А) оң санС) бүтін санД) 5
 А) теріс санВ) рационал сан
А) теріс санВ) рационал сан
Ах+Вх+Сz+5=0 және 2x-3y+z+5=0 жазықтықтары А,В,С-ның сәйкес параллель мәндері: -6,9,-3
 айқындалмаған функциясының
айқындалмаған функциясының  туындысы:
туындысы: 
Айнымалылары ажыратылатын дифференциалдық теңдеу: А)  В)
В) 
Айнымалылары ажыратылатын дифференциалдық теңдеу: C)  E)
E) 
Айнымалылары ажыратылатын дифференциалдық теңдеу А)  В)
В) 
Ақиқат емес оқиғаның ықтималдығы неге тең. A)0 D)0/3 G)0/5
Ақиқат оқиғаның ықтималдығы неге тең? A)1 C)  E)2/2
E)2/2
Алты ұпайдың пайда болу ықтималдығы 1/6-ға тең болса, онда пайда болмау ытималдығы неге тең :A)5/6 C)  F)
F) 
Анықталмаған коэффициенттер (жай бөлшектерге жіктеу) тәсілімен табылатын интеграл:  ;
; 
Анықтауышты есепте:  : 10/2; 5; 25/5
: 10/2; 5; 25/5
Анықтауышты есепте:  : - 12/2
: - 12/2
Анықтауышты есепте  А) -12В) -48/4С) -24/2
А) -12В) -48/4С) -24/2
Анықтауышты есепте  А) 88/2; 44
А) 88/2; 44
Анықтауышты есепте:  B)
B)  C)
C) 
Анықтауышты есепте:  B)
B)  D)
D)  F)
F) 
Анықтауышты есепте:  А) 20/2 * В)30/3*С)30/3
А) 20/2 * В)30/3*С)30/3
Анықтауышты есепте: 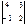 А) 22/2В) 33/3С) 11
А) 22/2В) 33/3С) 11
Анықтауышты есепте:  А) 24/2В) 48/4С)12
А) 24/2В) 48/4С)12
Анықтауышты есепте:  : В) 88/2
: В) 88/2
Анықтауышты есептеңіз.  A) 44 B)88/2 C)132/3
A) 44 B)88/2 C)132/3
Анықтауышты есептеңіз.  A) 44 D)88/2 G)132/3
A) 44 D)88/2 G)132/3
Анықтауышты есептеңіз.  A) 5 B)25/5 C)10/2
A) 5 B)25/5 C)10/2
Анықтауышты есептеңіз.  A) 60/2 B) 30 C) 120/40
A) 60/2 B) 30 C) 120/40
Анықтауышты есептеңіз.  A)10 B)20/2 C)30/3
A)10 B)20/2 C)30/3
Анықтауышты есептеңіз.  A)26 B)52/2 C)78/3
A)26 B)52/2 C)78/3
Анықтауышты есептеңіз.  D)-12 F)-24/2H)-48/4
D)-12 F)-24/2H)-48/4
Анықтауышты есептеңіз. 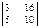 A) -50 B) -100/2 C) -300/3
A) -50 B) -100/2 C) -300/3
Анықтауышы есепте:  ; Е)20\2F)30\3
; Е)20\2F)30\3
 берілген гиперболаның эксцентриситетін тап: А) 5/4
берілген гиперболаның эксцентриситетін тап: А) 5/4
Баған матрица: 


Берілген сызықты теңдеулер жүйесін шешу арқылы y айнымалысының мәнін табыңыз:  A) 6 В)
A) 6 В)  С)
С) 
Берілгені:  A) -
A) -  B) -3
B) -3
Берілгені. D(Х)=4. Табыңыз:  .C)2 D)
.C)2 D)  G)4/2
G)4/2
Берілгені:  - гипербола. Табу керек оның жарты өстерін. A)
- гипербола. Табу керек оның жарты өстерін. A) 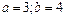 В)
В)  С)
С) 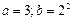
Берілгені:  - эллипс. Табу керек оның жарты өстерін. А)
- эллипс. Табу керек оның жарты өстерін. А)  В)
В)  С)
С) 
Берілгені: 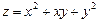 . Табыңыз:
. Табыңыз:  C)2 E)4/2 H)6/3
C)2 E)4/2 H)6/3
Берілгені:  . Табыңыз:
. Табыңыз:  . А) -20 C)-40/2 D)-60/3
. А) -20 C)-40/2 D)-60/3
Берілгені:  табу керек:
табу керек:  А) 2В) 4/2С) 6/3
А) 2В) 4/2С) 6/3
Берілгені:  . Нүктесіндегі
. Нүктесіндегі  мәнін табыңыз: C)4 D)
мәнін табыңыз: C)4 D) 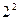 G)
G) 
Берілгені:  . Нүктесіндегі
. Нүктесіндегі 
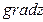 -ті табыңыз: A)
-ті табыңыз: A)  D)
D)  F)
F) 
Берілгені: 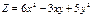 . Табу керек:
. Табу керек:  А) 24/2В) 12;36/3
А) 24/2В) 12;36/3
Берілгені:  . Табу керек:
. Табу керек:  - А)
- А)  В) -3
В) -3
Берілгені: 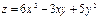 . Табыңыз:
. Табыңыз:  A) 12 C)24/2 D)36/3
A) 12 C)24/2 D)36/3
Берілгені:  . Табыңыз:
. Табыңыз:  A)4 C)
A)4 C)  F)
F) 
Берілгені:  . Табыңыз:
. Табыңыз:  D)-3 E)-
D)-3 E)-  H)-6/2
H)-6/2
Берілгені:  .Табыңыз:
.Табыңыз:  .А) -40 E)-80/2 H)-120/3
.А) -40 E)-80/2 H)-120/3
Берілгені: А=  , В=
, В=  . Берiлген матрицалардың көбейтіндісін тап. A)
. Берiлген матрицалардың көбейтіндісін тап. A) 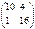 C)
C)  F)
F) 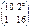
Берілгені: А=  , В=
, В=  . Берiлген матрицалардың көбейтіндісін тап. A)
. Берiлген матрицалардың көбейтіндісін тап. A) 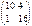 C)
C)  F)
F) 
Берілгені: А=  . Берiлген матрицаның А2 тап. A)
. Берiлген матрицаның А2 тап. A)  B)
B)  C)
C) 
Берілгені: А= 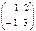 . Берiлген матрицаның А2 тап. A)
. Берiлген матрицаның А2 тап. A)  B)
B)  C)
C) 
Берілгені:  табу керек:
табу керек:  А) 12В) 36/3С) 24/2
А) 12В) 36/3С) 24/2
Берілгені:  табу керек:
табу керек:  А) 4/2В) 2С) 6/3
А) 4/2В) 2С) 6/3
Берілгені: 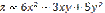 табу керк
табу керк  : С) 24/2D) 12
: С) 24/2D) 12
Берілгені:  табу керек:
табу керек:  A)4\2C)6\3D)2
A)4\2C)6\3D)2
Бірінші ретті сызықтық дифференциалдық теңдеу: B)  C)
C) 
Бірінші ретті сызықтық дифференциалдық теңдеу: В)  С)
С) 
Бірінші ретті сызықтық дифферециалдық теңдеу: А)  / В)
/ В) 
В) 2/10
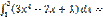 В) бүтін сан
В) бүтін сан
Векторлардың компланарлық шарты: A)осы векторлардан құрылған параллелепипедтің көлемі кез –келген оң санға теңC) осы векторлардан құрылған параллелепипедтің көлемі 1-ге теңF)осы векторлардан құрылған пирамиданың көлемі 1-ге тең
Векторлардың компланарлық шарты: А) осы векторлардан құрылған параллелипедтің көлемі кез-келген оң санға теңС) осы векторлардан құрылған параллелипедтің көлемі 1-ге теңЖ) осы векторлардан құрылған пирамиданың көлемі 1-ге тең
Векторларының көбейтіндісінің қасиеті:  ;
;

 векторының модулiн тап. B)
векторының модулiн тап. B)  D)
D)  E)
E) 
 векторының модулін тап А) 2 векторының ұзындығын табыңдар.B)13 D)26/2 H)39/3
векторының модулін тап А) 2 векторының ұзындығын табыңдар.B)13 D)26/2 H)39/3
Гармоникалық қатардың түрі: A) 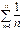 E)
E)  G)
G) 
Д) 3/10
Даламбер белгісі бойынша қатар  : С)жинақты,өйткені
: С)жинақты,өйткені  E)жинақты
E)жинақты
Даламбер белгісі бойынша қатар  А) жинақтыВ) жинақты, өйткені
А) жинақтыВ) жинақты, өйткені 
Даламбер белгісі бойынша қатар  А) жинақты, өйткені
А) жинақты, өйткені  В) жинақты
В) жинақты
Дәрежелік қатардың 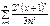 жалпы мүшесі келесі өрнек болады: A)
жалпы мүшесі келесі өрнек болады: A)  C)
C) 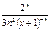 G)
G) 
Дәрежелік қатардың  жалпы мүшесінің коэффициенті тең:A )
жалпы мүшесінің коэффициенті тең:A )  G)
G)  H)
H) 
Дәрежелік қатардың  жалпы мүшесі келесі функция болады: D)
жалпы мүшесі келесі функция болады: D)  G)
G)  H)
H) 
 дәрежелік қатарының жинақтылық радиусын тең: A)
дәрежелік қатарының жинақтылық радиусын тең: A) 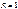 C)
C)  E)
E) 
Дисперсия 1/36 - ке тең болса, онда орташа квадраттық ауытқуды табыңыз. B)1/6 E)  G)1/
G)1/ 
 дифференциалдық теңдеуінің реті тең: D)4 F)
дифференциалдық теңдеуінің реті тең: D)4 F)  H)
H) 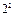
Е) 1/10
Егер  болса,
болса,  табу керек: C)2 E)4/2 H)6/3
табу керек: C)2 E)4/2 H)6/3
Егер  функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: B)
функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: B)  ;C) 0;
;C) 0;  ;
;  ;ln 1
;ln 1
Егер 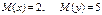 берілген болса, онда
берілген болса, онда  кездейсоқ шаманың математикалық үмітін табыңыз. B)3 F)
кездейсоқ шаманың математикалық үмітін табыңыз. B)3 F)  H)
H) 
Егер  берілген болса, онда
берілген болса, онда  кездейсоқ шаманың математикалық үмітін табыңыз. A)-4 D)-8/2 G)-12/3
кездейсоқ шаманың математикалық үмітін табыңыз. A)-4 D)-8/2 G)-12/3
Егер  болса,
болса,  табу керек: A)8/3 C)16/6 E)24/9
табу керек: A)8/3 C)16/6 E)24/9
Егер 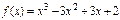 болса,
болса,  табу керек: B)3 D)6/2 G)9/3
табу керек: B)3 D)6/2 G)9/3
Егер  болса,
болса,  табу керек: A) 2/9 D)4/18 G)6/27
табу керек: A) 2/9 D)4/18 G)6/27
Егер  болса, у¢(1) табу керек: B)5 E)15/3 G)10/2
болса, у¢(1) табу керек: B)5 E)15/3 G)10/2
Егер  функциясы біртекті болса, онда оның біртектілік дәрежесін анықтаңыз. B)0 D)
функциясы біртекті болса, онда оның біртектілік дәрежесін анықтаңыз. B)0 D) 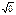 F)0/2
F)0/2
Егер  функциясы біртекті болса, онда оның біртектілік дәрежесін анықтаңыз. B)0 D)
функциясы біртекті болса, онда оның біртектілік дәрежесін анықтаңыз. B)0 D)  E)3
E)3
Егер  функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: А) 0В)
функциясы біртекті болса, онда оның біртектілік дәрежесін табу керек: А) 0В) 
Егер f(x) = 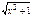 болса,
болса, 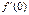 табу керек: A) 0 C)0/9 G)0/6;ln 1
табу керек: A) 0 C)0/9 G)0/6;ln 1
Егер  болса,
болса,  табу керек: A) 4 G)8/2 H)12/3
табу керек: A) 4 G)8/2 H)12/3
Екі белгісізі бар сызықтық теңдеуді шешіңіз  : А) (2,-2) В) (4/2,-4/2) С) (6/3,-6/3)
: А) (2,-2) В) (4/2,-4/2) С) (6/3,-6/3)
Екі белгісізі бар сызықтық теңдеуді шешіңіз  : A)(2,-2) B)(4/2,-4/2) C)(6/3,-6/3)
: A)(2,-2) B)(4/2,-4/2) C)(6/3,-6/3)
Екінші ретті дифференциалдық теңдеу: у2+ху2=7; 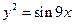
Екінші ретті сызықтық дифференциалдық теңдеудің  сипаттаушы теңдеуінің түбірлері: к1=-4, к2=-1; екі түбірі де бүтін сан; екі түбірі де теріс сан; k1=-20·22,k2=-20;k1=-log224, k2=-log22
сипаттаушы теңдеуінің түбірлері: к1=-4, к2=-1; екі түбірі де бүтін сан; екі түбірі де теріс сан; k1=-20·22,k2=-20;k1=-log224, k2=-log22
Есепте:  :
: 
Есепте:  : 16/2; 8
: 16/2; 8
Есепте:  ;
; 
Есепте:  : 15/10
: 15/10
Есепте  6/3; 4/2; 2
6/3; 4/2; 2
Есепте:  : 1/2; 2/4
: 1/2; 2/4
Есепте  А) 2,5В) 5/2
А) 2,5В) 5/2
Есепте:  A)
A) 
Есепте:  C)
C) 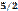
Есепте:  B)
B)  C)
C) 
Есепте 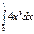 А) 0,1*10
А) 0,1*10
Есепте  А) -14В) -28/2С) -42/3
А) -14В) -28/2С) -42/3
Есепте  А) 1В) 2/2С) 8/8
А) 1В) 2/2С) 8/8
Есепте:  : 20/2
: 20/2
Есепте  А) 45/3В) 15
А) 45/3В) 15
Есепте 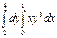 А) 6
А) 6  В)
В)  С) 30
С) 30
 есепте:
есепте:  A)-10/8 C) -1,25
A)-10/8 C) -1,25
Есепте:  : 2/2
: 2/2
Есепте:  А) 2/2В) 1С) 8/8
А) 2/2В) 1С) 8/8
Есепте:  А) 24/3
А) 24/3
Есепте:  А) 30/8В) 15/4С) 45/12
А) 30/8В) 15/4С) 45/12
Есепте:  А) 8В) 24/3С) 16/2
А) 8В) 24/3С) 16/2
Есепте:  В) 2/2С) 8/8
В) 2/2С) 8/8
Есепте:  F)
F) 
Есепте:  А)
А)  В)
В) 
Есепте:  : 12,8; 64/5
: 12,8; 64/5
Есепте:  : 124/10
: 124/10
Есептеѕіз:  A) 19 G)38/2 H)57/3
A) 19 G)38/2 H)57/3
Есептеңіз. 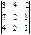 A) 0 C)0/7 H)0/9
A) 0 C)0/7 H)0/9
Есептеңіз. 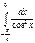 A) 1 C)6/6 G)5/5
A) 1 C)6/6 G)5/5
Есептеңіз. 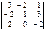 A) –12 E)-24/2 H)-36/3
A) –12 E)-24/2 H)-36/3
Есептеңіз. 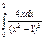 A) 8/9 D)16/18 G)24/27
A) 8/9 D)16/18 G)24/27
Есептеңіз.  D)41 E)82/2 H)123/3
D)41 E)82/2 H)123/3
Есептеңіз.  A) p/3 C)2 p/6 H) 3p/9
A) p/3 C)2 p/6 H) 3p/9
Есептеңіз. 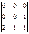 A) 0 C)0/7 H)0/9
A) 0 C)0/7 H)0/9
Есептеңіз.  A) –10 C)-20/2 E)-30/3
A) –10 C)-20/2 E)-30/3
Есептеңіз.  A) 12,8 D)128/10 G)64/5
A) 12,8 D)128/10 G)64/5
Есептеңіз.  A) –14 D)-28/2 G)-42/3
A) –14 D)-28/2 G)-42/3
Есептеңіз.  A) -2/3 B)-4/6 C)-8/12
A) -2/3 B)-4/6 C)-8/12
Есептеңіз.  A) 24 C)48/2 E)72/3
A) 24 C)48/2 E)72/3
Есептеңіз.  A) –28 B)-56/2 C)-84/3
A) –28 B)-56/2 C)-84/3
Есептеңіз.  A) 6 C)12/2 E)18/3
A) 6 C)12/2 E)18/3
Есептеңіз.  A) 61 B)122/2 E)183/3
A) 61 B)122/2 E)183/3
Есептеңіз.  A) -70 C)-140/2 G)-210/3
A) -70 C)-140/2 G)-210/3
Есептеңіз.  A) 8 C)16/2 E)24/3
A) 8 C)16/2 E)24/3
Есептеңіз.  C)2 E)4/2 H)6/3
C)2 E)4/2 H)6/3
Есептеңіз.  C)2 E)4/2 H)6/3
C)2 E)4/2 H)6/3
Есептеңіз. 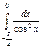 D)1 G)2/2 H)8/8
D)1 G)2/2 H)8/8
Есептеңіз.  A) 14/3 B)28/6 E)42/9
A) 14/3 B)28/6 E)42/9
Есептеңіз.  A) 3/8 C)6/16 E)9/24
A) 3/8 C)6/16 E)9/24
Есептеңіз.  A) 4,5 G)45/10 H)9/2
A) 4,5 G)45/10 H)9/2
Есептеңіз.  A) 66 D)132/2 G)198/3
A) 66 D)132/2 G)198/3
Есептеңіз.  A) 8/9 B)24/27 H)16/18
A) 8/9 B)24/27 H)16/18
Есептеңіз:  A) 0,5 E)1/2 H)2/4
A) 0,5 E)1/2 H)2/4
Есептеңіз: 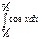 A) 0,5 E)1/2 H)2/4
A) 0,5 E)1/2 H)2/4
Есептеңіз:  A) 0,5 E)1/2 H)2/4
A) 0,5 E)1/2 H)2/4
Есептеңіз:  A) 0,5 E)1/2 H)2/4
A) 0,5 E)1/2 H)2/4
Есептеңіз:  A) 16 D)32/2 G)48/3
A) 16 D)32/2 G)48/3
Есептеңіз:  A) 2,5 C)25/10 H)5/2
A) 2,5 C)25/10 H)5/2
Есептеңіз:  A) 5 B)10/2 C)15/3
A) 5 B)10/2 C)15/3
Есептеңіз:  A) 8/3 G)16/6 H)24/9
A) 8/3 G)16/6 H)24/9
Есептеңіз:  B)15/4 D)30/8 G)45/12
B)15/4 D)30/8 G)45/12
Есептеңіз:  C)2 E)4/2 H)6/3
C)2 E)4/2 H)6/3
Есептеңіз: 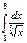 C)9/2 E)
C)9/2 E)  H)
H) 
Есепте  С) -28/2
С) -28/2
Жазықтықтың жалпы теңдеуін көрсетіңіз: А)  В)
В)  С)
С) 
Жазықтықтың жалпы теңдеуін көрсетіңіз: A)  B)
B)  C)
C) 
 және
және  векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын
векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын  векторын айтады В)
векторын айтады В)  векторына да
векторына да  векторына да перпендикулярС) ұзындығы
векторына да перпендикулярС) ұзындығы  және
және  векторларынан құрылған параллелограммның ауданына теңД) ұзындығы
векторларынан құрылған параллелограммның ауданына теңД) ұзындығы  және
және  векторларынан құрылған үшбұрыштың ауданына тең
векторларынан құрылған үшбұрыштың ауданына тең
 және
және  векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын
векторларының векторлық көбейтіндісі деп төмендегі шарттарды қанағаттандыратын  векторын айтады: А)
векторын айтады: А)  векторына да,
векторына да,  векторына да перпендикуляр В) ұзындығы
векторына да перпендикуляр В) ұзындығы  және
және  векторларынан құрылған параллелограммның ауданына теңС) осы векторлармен реттелген оң үштік құрайды
векторларынан құрылған параллелограммның ауданына теңС) осы векторлармен реттелген оң үштік құрайды
 және
және  нүктелері арқылы өтетін түзудің бұрыштық коэффициентін табу керек: А)
нүктелері арқылы өтетін түзудің бұрыштық коэффициентін табу керек: А)  В)2С)
В)2С) 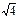
 және
және  нүктелері берілген.
нүктелері берілген.  векторының ординатасы: А)-4
векторының ординатасы: А)-4
 және
және  нүктелерінің арақашықтығын табу керек: А) 9/3В) 3
нүктелерінің арақашықтығын табу керек: А) 9/3В) 3
Жазықтықтағы кесіндіні берілген 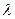 қатынаста бөлетін нүктенің координатасы:
қатынаста бөлетін нүктенің координатасы:  ,
, 
Жәшікте 4 ақ және 5 қызыл шар бар. Кездейсоқ жағдайда бір шар алынды. Алынған шардың қызыл болу ықтималдығы қандай. А)5/9  В)10/18 G)15/27
В)10/18 G)15/27
Жәшікте 4 ақ, 3 сары және 5 қызыл шар бар. Кездейсоқ жағдайда бір шар алынды. Алынған шардың ақ болу ықтималдығы қандай. А)1/3 В)2/6 G)4/12
Жәшікте 5 боялған деталь бар. Кездейсоқ алынған детальдің боялған болу ықтималдығын табыңыз. A)1 D)  G)
G) 
Жәшікте 8 деталь бар, оның алтауы боялған. Құрастырушы таңдамай 5 деталь алады. Алынған детальдардың ішінде 3 боялған болу ықтималдығын табу керек. A)5/14 D) 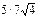 F)
F) 
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалп мүшесі: А)  ; В)
; В) 
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалпы мүшесі: А)  В)
В) 
Жинақтылыққа Даламбер белгісімен зерттелетін қатардың жалпы мүшесі: А)  В)
В) 
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі: B)  G)
G) 
Жинақтылыққа Кошидің радикалдық белгісімен зерттелетін қатардың жалпы мүшесі: А)  В)
В) 
Жинақтылыққа Лейбниц белгісімен зерттелетін қатардың жалпы мүшесі: С) 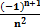 Е)
Е) 
Жинақтылыққа Лейбниц белгісімен зерттелетін қатардың жалпы мүшесі А)  В)
В) 
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі: D)  G)
G) 
Жинақтылықтың қажетті белгісі орындалатын қатардың жалпы мүшесі: Д)  Е)
Е)  З)
З) 
Жинақтылықтың қажетті шарты орындалатын қатар:  ;
;  ;
; 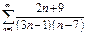
Жұп та емес, тақ та емес функция: А) 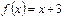 Ж)
Ж) 
Жұп та емес, тақ та емес функциялар: D) 
Жұп функция: А)  В)
В) 
Жұп функция: А)  В)
В)  С)
С)  Д)
Д) 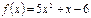
Жұп функция: C)  D)
D) 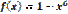
Интеграл:  :
:  ;
;  ;
; 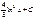
Интегралды есепте:  :
:  ;
;  ;
; 
Интегралды есепте:  , мұндағы – Ω аймағы у=0, х=1, у=х2 B)9/5
, мұндағы – Ω аймағы у=0, х=1, у=х2 B)9/5  C)3
C)3  G)9/20
G)9/20
Интегралды есепте:  мұндағы -
мұндағы -  аймағы, у=0, х=1, у=х2: 1/0,1*120;
аймағы, у=0, х=1, у=х2: 1/0,1*120; 
Интегралды есепте:  , мұндағы -
, мұндағы -  аймағы А) 9/20В)
аймағы А) 9/20В)  С)
С) 
Интегралды есепте:  :
: 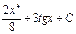 ;
; 
Интегралды есепте:  А)
А)  В)
В)  С)
С) 
Интегралды есептеңіз:  C)0 D)
C)0 D)  F)
F) 
Интегралды есептеңіз:  A)
A)  C)
C)  E)
E) 
Интегралды есептеңіз:  A)
A) 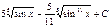 D)
D)  F)
F) 
Интегралды есептеңіз: 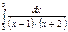 B)
B)  F)
F)  H)
H) 
Интегралды табыңыз.  C)2 E)4/2 H)6/3
C)2 E)4/2 H)6/3
Интегралды табыңыз:  . A)
. A)  G)
G)  H)
H) 
Интегралды табыңыз: 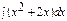 . A)
. A)  G)
G)  H)
H) 
Интегралды табыңыз:  . А)
. А)  G)
G) 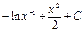 H)
H) 
Интегралды табыңыз:  A)
A) 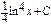 G)
G)  H)
H) 
Интегралды табыңыз:  A) -cos(lnx)+C G) -2/2cos(lnx)+C H) -3/3cos(lnx)+C
A) -cos(lnx)+C G) -2/2cos(lnx)+C H) -3/3cos(lnx)+C
Интегралды табыңыз:  .A)
.A) 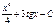 G)
G)  H)
H) 
Интегралды табыңыз: 
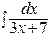 .A)
.A)  G)
G)  H)
H) 
Интегралды табыңыз:  : А) х3/3+lnx+С G) 2х3/6+lnx+С H) 4х3/12+lnx+С
: А) х3/3+lnx+С G) 2х3/6+lnx+С H) 4х3/12+lnx+С
Квадрат үшмүшелікте толық квадратты ажырату тәсілімен табылатын интеграл: А)  В)
В) 
Кездейсоқ шама Х мына үлестіру функциялары берілген. 
Келесі сызықтармен шектелген фигураның ауданын табу керек:у=х2; х=0; х=3; у=0: 9; 27/3; 18/2
Келесі сызықтармен шектелген фигураның ауданын табу керек:  А) 18/2В) 27/3С) 9
А) 18/2В) 27/3С) 9
Келесі сызықтармен шектелген фигураның ауданын табыңыз: у=5х, х=2, у=0: D)30/3E)10F)40/4
Кеңістіктегі проекциядағы түзу теңдеуі: x-a=mz y-b=nz. x=mz+a y=nz+b
Координаталардың бас нүктесінен  жазықтығына дейінгі қашықтықты табыңыз. A) 25 В)
жазықтығына дейінгі қашықтықты табыңыз. A) 25 В)  С)
С) 
Кошидің радикалдық белгісі бойынша қатар  : A)жинақсызD)жинақсыз,өйткені q
: A)жинақсызD)жинақсыз,өйткені q  F)жинақсыз, өйткені
F)жинақсыз, өйткені 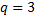 ;жинақсыз,өйткені q=e
;жинақсыз,өйткені q=e
Кошидің радикалдық белгісі бойынша қатар  : B) жинақсызD) жинақсыз,өйткені
: B) жинақсызD) жинақсыз,өйткені  F) жинақсыз, өйткені
F) жинақсыз, өйткені 
Кошидің радикалдық белгісі бойынша қатар  А) жинақсыз, өйткені
А) жинақсыз, өйткені  В) жинақсызС) жинақсыз, өйтккені
В) жинақсызС) жинақсыз, өйтккені 
Кошидің радикалдық белгісі бойынша қатар  А) жинақсыз, өйткені
А) жинақсыз, өйткені  В) жинақсыз, өйткені
В) жинақсыз, өйткені 
Кошидің радикалдық белгісі бойынша қатар  А) жинақсызВ) жинақсыз, өйткені
А) жинақсызВ) жинақсыз, өйткені 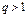
Кошидің радикалдық белгісі бойынша қатар: 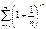 А) жинақсызВ) жинақсыз, өйткені
А) жинақсызВ) жинақсыз, өйткені 
Крамер формуласын көрсет. А) Date: 2016-11-17; view: 893; Нарушение авторских прав В)
В)