
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тесты для самопроверки
|
|
1. Коэффициент детерминации 
 = 0,85. Это означает:
= 0,85. Это означает:
а) при увеличении факторного признака на единицу результативный признак изменится на 0,85 единицы;
б) доля вариации результата за счёт фактора, в общей вариации результата, составляет 85%;
в) при увеличении факторного признака на 1% результативный признак изменится на 0,85 %.
2. Имеется модель регрессии 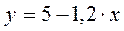 .Известны среднеквадратические отклонения для переменных и количество наблюдений:
.Известны среднеквадратические отклонения для переменных и количество наблюдений: 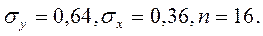
Вычислите коэффициент корреляции и сделайте вывод относительно тесноты связи между y и x:
а) 0,9 теснота связи сильная, зависимость прямая;
б) 0,675 теснота связи средняя, зависимость прямая;
в) -0,675 теснота связи средняя, зависимость обратная;
г) 0,9 теснота связи сильная, зависимость обратная.
3. Для парной линейной регрессии, построенной на 30 наблюдениях, число степеней свободы, соответствующее сумме квадратов отклонений, объясненной регрессией, составляет:
а) 30; б) 1; в) 39; г) 38; д) 2.
4. Экономический смысл коэффициента регрессии 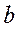 :
:
а) оценивает абсолютное изменение результата при изменении фактора на 1 единицу;
б) оценивает относительное изменение результата при изменении фактора на 1 единицу;
в) оценивает абсолютное изменение результата при изменении фактора на 1%;
г) абсолютное изменение фактора при изменении результата на 1 единицу.
5. Линейный коэффициент парной корреляции принимает значения:
а) от –1 до 0;
б) от 0 до +1;
в) от 0 до +∞;
г) от –1 до +1;
д) от -∞ до +∞;
е) от -∞ до ∞.
6. Нулевая гипотеза H0 это:
а) предположение о надёжности и статистической значимости показателя;
б) предположение о ненадёжности и статистической значимости показателя;
в) предположение о надёжности и статистической незначимости показателя;
г) предположение о ненадёжности и статистической незначимости показателя.
- Коэффициент детерминации R2 равен 0,952. Какова доля случайной компоненты в общей дисперсии yt?
- Приведите к линейному виду следующую функцию:
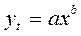
Что означает 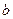 ?
?
- Значение индекса корреляции для модели
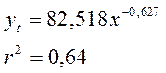
составляет:
а) 0,64 б) -0,627 в) 0,642) 0,8
- Выражение вида
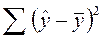 называется:
называется:
а) остаточной суммой квадратов отклонений
б) общей суммой квадратов отклонений
в) суммой квадратов отклонений, объясненной регрессией
- Уравнениями, линейными по параметрам, но нелинейными по переменным являются:
а) 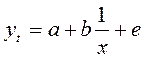
б) 
в) 
- Коэффициент регрессии будет значим, если:
а) в доверительный интервал коэффициента регрессии не входит ноль;
б) в доверительный интервал коэффициента регрессии входит ноль.
- Для уравнения регрессии
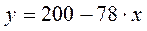 выберите отклонение фактического значения от расчетного для точки с координатами (2;50):
выберите отклонение фактического значения от расчетного для точки с координатами (2;50):
а) 58;
б) 6;
в) 4;
г) 44.
- Для изучения зависимости затрат на производство y(тыс. руб.) от объема выпуска x (шт.) по 8 наблюдениям построены варианты уравнения регрессии и рассчитаны коэффициенты детерминации. Выберите модель регрессии, параметры которой при независимых переменных имеют четкую экономическую интерпретацию.
а) 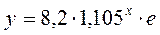

б) 
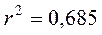
в) 
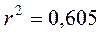
г) 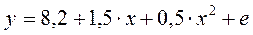
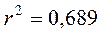
- Множественный коэффициент корреляции принимает значения:
а) от –1 до 0;
б) от 0 до +1;
в) от 0 до +∞;
г) от –1 до +1.
- Значения коэффициентов регрессии множественной модели - bj:
а) всегда можно сравнить, т.к. это абсолютные оценки влияния факторов 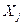 на результат;
на результат;
б) можно сравнить только при условии одинаковых единиц измерения факторов 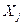 ;
;
в) можно сравнивать, если у них совпадают знаки при коэффициентах регрессии bj;
г) сравнивать их нельзя, для этой цели рассчитываются относительны показатели – коэффициенты эластичности или 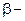 коэффициенты;
коэффициенты;
д) можно сравнивать, если у них отличаются знаки при коэффициентах регрессии bj.
- Проверка наличия коллинеарных факторов в эконометрической модели
 основана на рассмотрении коэффициента корреляции между
основана на рассмотрении коэффициента корреляции между
| a) y и { x1; x2 } |
| b) y и x2 |
| c) x1 и x2 |
| d) y и x1 |
- Переменные, принимающие значения 0 и 1, которые вводят в модель множественной регрессии для количественного задания некоторого качественного признака, называются:
| a) зависимыми |
| b) коллинеарными |
| c) независимыми d) фиктивными |
- В регрессионной модели
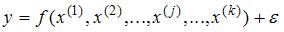 . Количество зависимых переменных равно:
. Количество зависимых переменных равно:
| a) 1 |
| b) k + 1 |
| c) 2 |
| d) k |
- В регрессионной модели,
 построенной по 25 наблюдениям, остаточное число степеней свободы равно:
построенной по 25 наблюдениям, остаточное число степеней свободы равно:
| a) 25 |
| b) 4 |
| c) 21 |
| d) 20 |
- В регрессионной модели,
 построенной по 25 наблюдениям, общее число степеней свободы равно:
построенной по 25 наблюдениям, общее число степеней свободы равно:
| a) 25 |
| b) 4 |
| c) 21 |
| d) 20 |
- В регрессионной модели,
 построенной по 25 наблюдениям, факторное число степеней свободы равно:
построенной по 25 наблюдениям, факторное число степеней свободы равно:
| a) 25 |
| b) 4 |
| c) 21 |
| d) 20 |
- Исследуется зависимость
 . Построена матрица парных коэффициентов корреляции:
. Построена матрица парных коэффициентов корреляции:
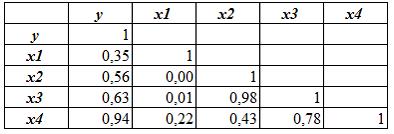
Одновременно в одно и то же уравнение регрессии, по причине коллинеарности, не могут быть включены факторы (укажите не менее двух вариантов ответа):
| a) x2 и x4 |
| b) x3 и x1 |
| c) x2 и x3 |
| d) x3 и x4 |
- Отбор факторов в эконометрическую модель линейного уравнения множественной регрессии можно проводить на основе (укажите не менее двух вариантов ответа):
| a) включения коллинеарных факторов в одно и то же уравнение |
| b) отбора более высоких значений коэффициентов регрессии модели в естественном масштабе переменных. |
| c) сравнения величины остаточной дисперсии до и после включения дополнительного фактора в уравнение |
| d) исключения одного из пары коллинеарных факторов из модели |
- Дана матрица парных коэффициентов корреляции:
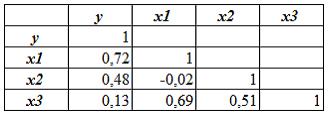
значениями тесноты связи между факторами (регрессорами) являются (укажите не менее двух вариантов ответа):
| a) 0,51 |
| b) 0,72 |
| c) –0,02 |
| d) 0,48 |
- Проблема мультиколлинеарности появится, если:
1. Коэффициент корреляции между факторами ≥ 0,7
2. Коэффициент условно-чистой регрессии ≥ 0,7
3. Коэффициент корреляции между факторами ≤0,7
4. Коэффициент условно-чистой регрессии ≤0,7
- Параметры при независимых переменных в степенной модели множественной регрессии являются:
1. абсолютными показателями силы связи и поэтому несопоставимы
2. относительными показателями силы связи и поэтому несопоставимы
3. относительными показателями силы связи и поэтому сопоставимы
4. показателями тесноты связи и поэтому сопоставимы
5. абсолютными показателями силы связи и поэтому сопоставимы
- Скорректированный коэффициент детерминации применяется для:
1. сравнения моделей с разным числом параметров
2. для характеристики тесноты связи рассматриваемого фактора на результат, при условии, что остальные факторы зафиксированы
3. сравнения факторов по силе их влияния на результат
4. для характеристики силы связи рассматриваемого фактора на результат, при условии, что остальные факторы зафиксированы
- Включая в модель новый фактор, мы предполагаем, что (указать не менее двух вариантов ответов):
1. он внесет существенный вклад в объяснение результата, то есть остаточная дисперсия должна уменьшиться
2. он внесет существенный вклад в объяснение результата, то есть остаточная дисперсия должна увеличиться
3. он внесет существенный вклад в объяснение результата, то есть факторная дисперсия должна уменьшиться
4. он внесет существенный вклад в объяснение результата, то есть факторная дисперсия должна увеличиться
- Постоянство дисперсии случайных остатков называют:
1. гомоскедастичностью остатков
2. мультиколлинеарностью
3. гетероскедастичностью остатков
- Непостоянство дисперсии случайных остатков называют:
1. гомоскедастичностью остатков
2. мультиколлинеарностью
3. гетероскедастичностью остатков
- Если при использовании теста Гольдфельда-Квандта F-фактическое больше табличного, то гипотеза об отсутствии гетероскедастичности
1. отклоняется
2. не отклоняется
- Метод Гольдфельда-Квандта используется для:
1. выявления мультиколлинеарности факторов
2. выявления гетероскедастичности
3. для характеристики значимости параметров при факторах
4. исключения гетероскедастичности
5. исключения мультиколлинеарности факторов
- Тест Парка используется для:
1. выявления мультиколлинеарности факторов
2. выявления гетероскедастичности
3. для характеристики значимости параметров при факторах
4. исключения гетероскедастичности
5. исключения мультиколлинеарности факторов
- Тест Уайта используется для:
1. выявления мультиколлинеарности факторов
2. выявления гетероскедастичности
3. для характеристики значимости параметров при факторах
4. исключения гетероскедастичности
5. исключения мультиколлинеарности факторов
- Тест Глейзера используется для:
1. выявления мультиколлинеарности факторов
2. выявления гетероскедастичности
3. для характеристики значимости параметров при факторах
4. исключения гетероскедастичности
5. исключения мультиколлинеарности факторов
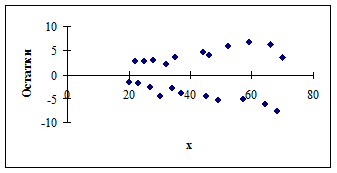
- Данный график свидетельствует:
1. о наличии мультиколлинеарности факторов
2. о наличии гетероскедастичности
3. об отсутствии мультиколлинеарности факторов
4. об отсутствии гетероскедастичности
- Решается вопрос о введении фиктивной переменной, характеризующей уровень квалификации. Пусть имеются три возможных степени квалификации: высшая, средняя, низкая. Число фиктивных переменных будет равно:
1. 1
2. 2
3. 3
- Тренд представляет собой:
1. это основная тенденция изменения уровней временного ряда;
2. это множество значений уровней временного ряда;
3. это аналитическое выражение в форме уравнения основной тенденции изменений уровней временного ряда;
4. это множество средних, рассчитанных из несколько смежных уровней временного ряда.
- Коэффициент автокорреляции отклонений, равный ─0,855:
 приводит к выводу:
приводит к выводу:
1. отклонения от тренда случайные величины; выявленный тренд устойчив, надёжен, статистически значим;
2. отклонения от тренда устойчивы, надёжны, статистически значимы, то есть, не являются случайными величинами; выявленный тренд не отличается устойчивостью и надёжностью;
3. отклонения от тренда тесно связаны, они не являются случайными величинами, форма тренда выбрана удачно и может использоваться при прогнозировании;
4. отклонения не находятся в тесной зависимости, являются случайными величинами, следовательно, тренд выявлен неудачно, но может быть использован при прогнозировании.
- Для выявления тренда используются нелинейные формы:
1. когда уровни временного ряда изменяются равномерно;
2. когда уровни временного ряда изменяются неравномерно;
3. когда равномерное и неравномерное изменение уровней чередуется;
4. когда изменения уровней не имеют устойчивой формы.
- Коэффициент Дарбина-Уотсона и автокорреляции отклонений от тренда:
1. всегда дают одинаково точную и информативную оценку корреляции отклонений;
2. коэффициент Дарбина-Уотсона даёт точную оценку всегда, а коэффициент автокорреляции – лишь иногда;
3. коэффициент Дарбина-Уотсона не даёт точной оценки только в случае, когда его значения находятся в критической зоне, а коэффициент автокорреляции – лишь иногда;
4. коэффициент Дарбина-Уотсона даёт точную оценку, исключая случаи, когда он принимает значения из критической зоны, а коэффициент автокорреляции даёт точную оценку всегда;
5. ни тот, ни другой коэффициенты не дают точной оценки наличия автокорреляции отклонений.
- В аддитивной модели компоненты временного ряда связаны следующим образом:
а) T+P+E;
б) T×P×E;
в) T÷P÷E.
- Обобщенный МНК применяется:
а) для исключения мультиколлинеарности;
б) для исключения тенденции;
в) для выявления автокорреляции в уровнях динамического ряда;
г) для оценки параметров уравнения при наличии автокорреляции в остатках.
- Если временной ряд характеризуется постоянным абсолютным ускорением, то есть постоянными являются вторые разности, то для моделирования тенденции целесообразно использовать:
а) линейную функцию;
б) степенную функцию;
в) параболу второго порядка;
г) показательную функцию.
- Приведите к линейному виду следующую функцю:
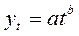
Что означает  ?
?
- Динамика прибыли (в млн. руб.) за ряд лет характеризуется уравнением вида:
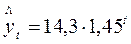
Это означает, что:
а) среднегодовой коэффициент роста составил 45%;
б) ежегодно прибыль возрастает в среднем на 45 млн. руб.;
в) данный параметр интерпретировать нельзя;
г) ежегодно прибыль возрастает в среднем на 14,5 млн. руб.;
д) ежегодно прибыль возрастает в среднем на 45%.
- Автокорреляционной функцией (АКФ) принято называть):
а) серию коэффициентов автокорреляции уровней ряда с последовательным увеличением величины лага;
б) серию коэффициентов автокорреляции остатков ряда с последовательным увеличением величины лага;
в) уравнение, характеризующее связь зависимой переменной от лаговых значений зависимой переменной.
- Изучать связь временных рядов на основе корреляции их уровней:
а) нецелесообразно, если в уровнях каждого ряда имеется тренд, то есть уровни не являются случайными, независимыми переменными;
б) допустимо, т.к. их тренды зависят от одного перечня факторных признаков;
в) допустимо, т.к. уровни временных рядов формируются в одно время и под действием единого перечня факторов;
г) нельзя, если временные ряды, построенные по разным признакам, несопоставимы.
- Для проверки статистической значимости уравнения линейной регрессии по F-критерию Фишера используется:
а) коэффициент эластичности;
б) коэффициент ранговой корреляции;
в) коэффициент детерминации;
г) относительная ошибка аппроксимации.
- Параметры
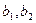 производственной функции (функции Кобба-Дугласа)
производственной функции (функции Кобба-Дугласа) 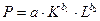 (где P – объем продукции, K - основной капитал, L - занятость) являются):
(где P – объем продукции, K - основной капитал, L - занятость) являются):
а) коэффициентами корреляции;
б) абсолютными показателями силы связи;
в) стандартизованными коэффициентами регрессии;
г) коэффициентами эластичности.
- С целью выявления периодических колебаний объема продажи товаров за 18 месяцев была рассчитана серия коэффициентов автокорреляции разных порядков: первого порядка (
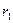 =0,851); второго порядка (
=0,851); второго порядка (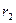 =0,828); третьего порядка (
=0,828); третьего порядка ( =1); четвертого порядка (
=1); четвертого порядка (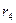 =0,819); пятого порядка (
=0,819); пятого порядка (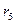 =0,769); шестого порядка (
=0,769); шестого порядка (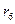 =1).
=1). - Для ряда характерна регулярная колеблемость уровней (периодические колебания) с........................лагом (укажите величину лага.
- Строится модель регрессии с учетом сезонного фактора по временным рядам за 5 лет с поквартальной разбивкой. Число фиктивных переменных, используемых в модели, будет равно:
а) 4;
б) 3;
в) 5;
г) 9.
Пример экзаменационной работы по дисциплине «Эконометрика (продвинутый уровень)»
Вариант 1
ЧАСТЬ II
1. Экономический смысл коэффициента регрессии 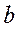 :
:
а) оценивает абсолютное изменение результата при изменении фактора на 1 единицу;
б) оценивает относительное изменение результата при изменении фактора на 1 единицу;
в) оценивает абсолютное изменение результата при изменении фактора на 1%;
г) абсолютное изменение фактора при изменении результата на 1 единицу.
2. Коэффициент детерминации 
 = 0,93. Это означает:
= 0,93. Это означает:
а) при увеличении факторного признака на единицу результативный признак изменится на 0,93 единицы;
б) доля вариации результата за счёт фактора, в общей вариации результата, составляет 93%;
в) при увеличении факторного признака на 1% результативный признак изменится на 0,93 %.
3. Коэффициент эластичности равен 0,37:
а) при увеличении факторного признака на единицу результативный признак изменится на 0,37 единицы;
б) доля вариации результата за счёт фактора, в общей вариации результата, составляет 37%;
в) при увеличении факторного признака на 1% результативный признак изменится на 0,37 %;
в) при увеличении факторного признака на 1% результативный признак изменится на 0,37 единиц;
г) при увеличении факторного признака на единицу результативный признак изменится на 0,37 %.
- В аддитивной модели компоненты временного ряда связаны следующим образом:
а) T+P+E; б) T×P×E; в) T÷P÷E.
- Обобщенный МНК применяется:
а) для исключения мультиколлинеарности;
б) для исключения тенденции;
в) для выявления автокорреляции в уровнях динамического ряда;
г) для оценки параметров уравнения при наличии автокорреляции в остатках.
- Если временной ряд характеризуется постоянным абсолютным ускорением, то есть постоянными являются вторые разности, то для моделирования тенденции целесообразно использовать:
а) линейную функцию;
б) степенную функцию;
в) параболу второго порядка;
г) показательную функцию.
- Приведите к линейному виду следующую функцию:
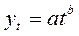
Что означает  ?
?
- Динамика прибыли (в млн. руб.) за ряд летхарактеризуется уравнением вида:
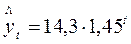 Это означает, что:
Это означает, что:
а) среднегодовой коэффициент роста составил 45%;
б) ежегодно прибыль возрастает в среднем на 45 млн. руб.;
в) данный параметр интерпретировать нельзя;
г) ежегодно прибыль возрастает в среднем на 14,5 млн. руб.;
д) ежегодно прибыль возрастает в среднем на 45%.
- Автокорреляционной функцией (АКФ) принято называть):
а) серию коэффициентов автокорреляции уровней ряда с последовательным увеличением величины лага;
б) серию коэффициентов автокорреляции остатков ряда с последовательным увеличением величины лага;
в) уравнение, характеризующее связь зависимой переменной от лаговых значений зависимой переменной.
- Изучать связь временных рядов на основе корреляции их уровней:
а) нецелесообразно, если в уровнях каждого ряда имеется тренд, то есть уровни не являются случайными, независимыми переменными;
б) допустимо, т.к. их тренды зависят от одного перечня факторных признаков;
в) допустимо, т.к. уровни временных рядов формируются в одно время и под действием единого перечня факторов;
г) нельзя, если временные ряды, построенные по разным признакам, несопоставимы.
- Для проверки статистической значимости уравнения линейной регрессии по F-критерию Фишера используется:
а) коэффициент эластичности;
б) коэффициент ранговой корреляции;
в) коэффициент детерминации;
г) относительная ошибка аппроксимации.
- Параметры
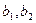 производственной функции (функции Кобба-Дугласа)
производственной функции (функции Кобба-Дугласа) 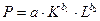 (где P – объем продукции, K - основной капитал, L - занятость) являются):
(где P – объем продукции, K - основной капитал, L - занятость) являются):
а) коэффициентами корреляции;
б) абсолютными показателями силы связи;
в) стандартизованными коэффициентами регрессии;
г) коэффициентами эластичности.
- С целью выявления периодических колебаний объема продажи товаров за 18 месяцев была рассчитана серия коэффициентов автокорреляции разных порядков: первого порядка (
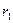 =0,851); второго порядка (
=0,851); второго порядка (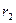 =0,828); третьего порядка (
=0,828); третьего порядка ( =1); четвертого порядка (
=1); четвертого порядка (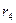 =0,819); пятого порядка (
=0,819); пятого порядка (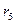 =0,769); шестого порядка (
=0,769); шестого порядка (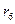 =1).
=1).
Для ряда характерна регулярная колеблемость уровней (периодические колебания) с........................лагом (укажите величину лага.
- Строится модель регрессии с учетом сезонного фактора по временным рядам за 5 лет с поквартальной разбивкой. Число фиктивных переменных, используемых в модели, будет равно:
а) 4; б) 3; в) 5; г) 9.
ЗАДАЧИ
Задача 1
По данным за 19 лет изучается зависимость рентабельности основного капитала (%) 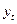 от оборачиваемости запасов (дней)
от оборачиваемости запасов (дней)  . Было получено следующее уравнение регрессии с включением фактора времени:
. Было получено следующее уравнение регрессии с включением фактора времени:
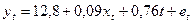
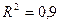
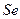
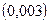
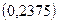
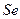 - стандартные ошибки параметров уравнения регрессии.
- стандартные ошибки параметров уравнения регрессии.
Задание.
- Оцените значимость модели в целом, а также отдельных ее параметров.
- Оцените автокорреляцию в остатках, если фактическое значение критерия Дарбина-Уотсона составило 2,4.
- Какова цель включения в данную модель фактора времени?
- Дайте интерпретацию коэффициентов регрессии.
Задача 2
По данным за три года (с разбивкой по кварталам) была построена следующая модель регрессии с включением в нее сезонного фактора, представленного в виде фиктивных переменных (z):

R2 =0,984
В скобках под каждым из параметров указаны фактические значения t- критерия Стьюдента.
Задание.
1. Дайте интерпретацию коэффициента детерминации. Какова доля случайной компоненты в общей дисперсии yt?
2. Что показывают параметры при фиктивных переменных в данном уравнении?
3. Напишите уравнение регрессии для каждого квартала.
Задача 3
По квартальным данным об объеме выпуска, млн.руб..(y) за период с 2006 по 2011гг. получены следующие результаты регрессионного анализа.
| r | 0,991033 | |||
| r-квадрат | 0,982146 | |||
| Наблюдения | ||||
| Дисперсионный анализ | ||||
| df | SS | MS | F | |
| Регрессия | ??? | 4,3939 | ??? | ??? |
| Остаток | ??? | 0,0799 | 0,0044 | |
| Итого | ??? | |||
| Коэффициенты | Стандартная ошибка | t-статистика | ||
| Y-пересечение | 0,604 | 0,0309 | 19,5187 | |
| t | 0,0813 | 0,0026 | ??? |
Задание
1. Напишите уравнение линейного тренда объема выпуска.
2. Рассчитайте недостающие показатели.
3. Дайте интерпретацию коэффициента регрессии.
4. Оцените достоверность уравнения в целом и параметров.
Date: 2016-06-06; view: 5044; Нарушение авторских прав