Понятие идеального газа

Идеальный газ – это модель реального газа, которая обладает следующими свойствами:

Молекулы пренебрежимо малы по сравнению со средним расстоянием между ними.

Молекулы ведут себя подобно маленьким твердым шарикам: они упруго сталкиваются между собой и со стенками сосуда, никаких других взаимодействий между ними нет.

Молекулы находятся в непрекращающемся хаотическом движении.

Все газы при не слишком высоких давлениях и при не слишком низких температурах близки по своим свойствам к идеальному газу. При высоких давлениях молекулы газа настолько сближаются, что пренебрегать их собственными размерами нельзя. При понижении температуры кинетическая энергия молекул уменьшается и становится сравнимой с их потенциальной энергией, следовательно, при низких температурах пренебрегать потенциальной энергией нельзя.

При высоких давлениях и низких температурах газ не может считаться идеальным. Такой газ называют реальным. (Поведение реального газа описывается законами, отличающимися от законов идеального газа.)

Когда была принята гипотеза А. Авогадро о том, что в киломоле любого вещества содержится одно и то же количество структурных единиц: 6,02 x 10²⁶кмоля = 6,02 x 10²³ моля, поскольку молярная масса воды M(H₂O) = 18 кг/кмоль, следовательно, в 18 литрах воды находится столько же молекул, сколько в 22,4 м³водяного пара. Это позволяет легко понять, что расстояние между молекулами газообразной воды (пара) значительно больше, в среднем на один порядок, чем в жидкой воде. Можно предположить, что это выполняется для любого вещества. Считая, что в газах молекулы движутся хаотически, можно вывести так называемое основное уравнение кинетической теории:

где Na – 6,02 x 10²⁶ кмоль = 6,02 x 10²³ моль – число Авогадро;

V_M – молекулярный объем = 22,4 м³;

m – масса одной молекулы;

v – скорость молекулы.

18. (1) Уравнение состояния идеального газа (иногда уравнение Клапейрона- Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа.

, где р – давление газа; V- объем газа; m – масса газа; М – молярная доля газа; R – универсальная газовая постоянная (R=8.31 Дж/моль*кг); Т – абсолютная температура газа в Кельвинах;

Отношение / в уравнении – это есть количество молей газа ().

(2) Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём, температура – остаются неизменными, а также процесс, протекающий без обмена теплоты с окружающей средой (адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно.

- Изотермический процесс: Температура газа постоянная (Т=const)

- Изобарный процесс: Давление газа постоянное (р=const)

- Изохорный процесс: Объём газа постоянный (V=const) - Адиабатич процесс: Протекает без обмена тепла с окр. средой ()

19. (1) Термодинамика или термодинамический подход – феноменологическое исследование явлений и свойств материальных тел, характеризуемых макроскопическими параметрами: P (давление), V (объем), T (температура) и другими. Основа подхода – 3 начала, или принципа, которые являются обобщением опыта. В этом подходе не выявляются микроскопические механизмы изучаемых явлений. Теплота, скажем, рассматривается как какое-то внутреннее движение, но при этом не конкретизируется какое.

(2) Теплота (Q) – это энергия, которая сообщается телу в процессе теплопередачи.

Внутренняя энергия (u) тела – это сумма кинетической энергии поступательного и вращательного движения частиц тела, и потенциальной энергии взаимодействия молекул между собой.

(3) Первое начало термодинамики: Кол-во теплоты, переданное системе, идёт на изменение внутренней энергии системы и на совершение работы системой.

20. Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c. c = Q / (mΔT).

Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры.

Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: C_V –молярная теплоемкость в изохорном процессе (V = const) и C_p – молярная теплоемкость в изобарном процессе (p = const).

В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует

Энергию эту можно представить как сумму трех слагаемых — кинетических энергий движения молекулы по трем взаимно перпендикулярным направлениям: 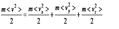,где v_x, v_y, v_z – составляющие скорости молекулы по трем осям координат. Полная хаотичность молекулярных движений позволяет считать, что средние значения кинетических энергий по трем направлениям равны друг другу:

Так как согласно основному уравнению кинетической теории

, то каждое из слагаемых равенства равно.Разделение кинетической энергии частицы на три независимые составляющие связано с тем, что частица рассматривается как свободная материальная точка, обладающая тремя степенями свободы. Числом степеней свободы механической системы называется число независимых координат, определяющих ее положение и конфигурацию в пространстве. Положение в пространстве материальной точки полностью определяется заданием значений трех ее координат. Координаты могут быть декартовы (задаются проекции на координатные оси радиус-вектора точки x, y, z), цилиндрические (задаются две линейные координаты и одна угловая), сферические (задаются две угловые координаты и одна линейная) и т. д. В любом случае положение точки в пространстве полностью определяется тремя независимыми числами. В соответствии с этим материальная точка имеет три степени свободы.Значит, на каждую степень свободы одноатомной молекулы приходится энергия, равная kT/2.

В статистической физике доказывается, что на любую степень свободы движения молекулы (поступательную, вращательную и т.д.) приходится одна и та же энергия, равная 1/2kТ. Это утверждение носит название закона равнораспределения энергии по степеням свободы.

В общем случае, когда молекула имеет iстепеней свободы, её кинетическая энергия

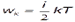
МАЙЕРА УРАВНЕНИЕ - ур-ние, устанавливающее связь между теплоёмкостями при пост, давлении Cp и пост, объёме С_V 1 кмоля идеального газа: 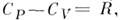где R -газовая постоянная.. Для произвольной массы т (кг) вещества в состоянииидеального газа M. у. записывается в виде: , где - молекулярная масса газа. M. у. можно получить из общего соотношения ,если учесть, что для идеального газа справедливо Клапейрона уравнение.

21. Адиабатическим называется процесс, при котором отсутствует теплообмен (Q= 0)между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. , Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

22 Цикл Карно состоит из четырёх стадий: Изотермическое расширение. В начале процесса рабочее тело имеет температуру Тн, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Qн. При этом объём рабочего тела увеличивается.

Адиабатическое (изоэнтропическое) расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты.

Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:

при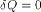

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно

.

Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику

.

Отсюда коэффициент полезного действия тепловой машины Карно равен

.

Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.

Поэтому максимальный КПД любой тепловой машины будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника.

23 Второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

Можно дать более краткую формулировку второго начала термодинамики: в про­цессах, происходящих в замкнутой системе, энтропия не убывает. Здесь существенно, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом (убывать, возрастать, оставаться постоянной). Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах в замкнутой системе энтропия всегда возрастает.

Формула Больцмана позволяет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Таким образом, формула Больцмана позволяет дать статисти­ческое толкование второго начала термодинамики. Оно, являясь статистическим зако­ном, описывает закономерности хаотического движения большого числа частиц, со­ставляющих замкнутую систему.

S=k*ln(P),

k = R/N = 1,38*10-23 Дж/К,

где k - фундаментальная мировая постоянная Больцмана;R = 8,31 Дж/(моль*К) - молярная газовая постоянная; N = 6,06*1023 моль-1 - число Авогадро;

Р - статистический вес: число способов осуществления данного состояния.

Параметр S - энтропия - служит мерой рассеяния энергии Вселенной, а Р - характеризует любые самопроизвольные изменения, эта величина относится к миру атомов, определяющих скрытый механизм изменения.

Укажем еще две формулировки второго начала термодинамики:

1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2) по Клаузиусу: невозможен круговой процесс, единственным результатом которо­го является передача теплоты от менее нагретого тела к более нагретому.

. Кроме того, показано, что если в замкнутой системе провести воображаемый процесс, противоречащий второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это же доказывает эквивалентность формулировки Клаузиуса (а следовательно, и Кельвина) и статистической формулировки, согласно которой энтропия замкнутой системы не может убывать.

24 Уравнение Ван-дер-Ваальса., для реальных газов необходимо учитывать размеры мо­лекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона—Менделеева (42.4) pVm=RT (для моля газа), описывающее иде­альный газ, для реальных газов непри­годны.Учитывая собственный объем молекул и сил межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальса (1837—1923) вывел уравнения состояния реального газа. Ван-дер-Ваальсом в урав­нение Клапейрона—Менделеева введены две поправки.1. Учет собственного объема молекул. Наличие сил отталкивания, которые про­тиводействуют проникновению в занятый молекулой объем других молекул, сводит­ся к тому, что фактический свободный объем, в котором могут двигаться молеку­лы реального газа, будет не Vm, a Vm -b, где b — объем, занимаемый самими молекулами. Объем b равен учетверенному соб­ственному объему молекул. Если, напри­мер, в сосуде находятся две молекулы, то центр любой из них не может при­близиться к центру другой молекулы на расстояние, меньшее диаметра d молеку­лы. Это означает, что для центров обеих молекул оказывается недоступным сфери­ческий объем радиуса d, т. е. объем, рав­ный восьми объемам молекулы, а в расче­те на одну молекулу — учетверенный объем молекулы.2. Учет притяжения молекул. Действие сил притяжения газа приводит к появле­нию дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутрен­нее давление обратно пропорционально квадрату молярного объема, т. е.p' = a/V2m, (61.1)где а— постоянная Ван-дер-Ваальса, ха­рактеризующая силы межмолекулярного притяжения, Vm — молярный объем.Вводя эти поправки, получим уравне­ние Ван-дер-Ваальса для моля газа (урав­нение состояния реальных газов):(p+a/V2m)(Vm-b)=RT.Для произвольного количества вещества v газа (v=т/М) с учетом того, что V = vVm, уравнение Ван-дер-Ваальса примет вид

где поправки а и b — постоянные для каж­дого газа величины, определяемые опыт­ным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).При выводе уравнения Ван-дер-Вааль­са сделан целый ряд упрощений, поэтому оно также весьма приближенное, хотя и лучше (особенно для несильно сжатых газов) согласуется с опытом, чем уравне­ние состояния идеального газа.Уравнение Ван-дер-Ваальса не единствен­ное уравнение, описывающее реальные газы. Существуют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности.

26.Распределение Максвелла молекул по скоростям. Наиболее вероятная средняя арифметическая и среднеквадратичная скорости молекул газа
Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале.скоростей остается неизменной. Необходимые измерения показали, что доля молекул , отнесенная к интервалу скорости Δ v, т.е. , имеет вид, показанный на рис. 3.3. Максвелл в 1859 г. теоретически на основании теории вероятности определил эту функцию. С тех пор она называется функцией распределения молекул по скоростям или законом Максвелла.Аналитически она выражается формулой

,

где m – масса молекулы, k – постоянная Больцмана. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема.Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой

или

.

Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул. Она рассчитывается по формуле:

.

Сопоставляя все три скорости:

1) наиболее вероятную ,

2) среднюю ,

3) среднюю квадратичную , – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная. Относительное число быстрых и медленных молекул мало (рис. 3.4).

При изменении температуры газа будут изменяться скорости движения всех молекул, а, следовательно, и наиболее вероятная скорость. Поэтому максимум кривой будет смещаться вправо при повышении температуры и влево при понижении температуры. Высота максимума не будет оставаться постоянной. Дело в том, что площадь заштрихованной фигуры численно равна доле общего числа молекул n, которую образуют молекулы со скоростями в указанном интервале. Общая площадь, ограниченная кривой распределения и осью абсцисс (скоростей), таким образом, равна единице и не меняется при изменении температуры (рис. 3.5). Поэтому высота максимума и меняется при изменении температуры.

Рис. 3.5

Кривые распределения молекул по скоростям начинаются в начале координат, асимптотически приближаются к оси абсцисс при бесконечно больших скоростях. Слева от максимума кривые идут круче, чем справа. То, что кривая распределения начинается в начале координат, означает, что неподвижных молекул в газе нет. Из того, что кривая асимптотически приближается к оси абсцисс при бесконечно больших скоростях, следует, что молекул с очень большими скоростями мало. Это легко объяснимо. Для того чтобы молекула могла приобрести при столкновениях очень большую скорость, ей необходимо получить подряд много таких столкновений, при которых она получает энергию, и ни одного столкновения, при котором она ее теряет. А такая ситуация маловероятна.

Date: 2016-06-06; view: 1120; Нарушение авторских прав