Картеровы и гащюцевы подгруппы разрешимых групп

Курсовая работа

по дисциплине «Геометрия и алгебра»

Классы Фиттинга

Выполнил:

студент 3 курса 2 группы

физико-инженерного факультета

Пеккинен Ян Александрович

Научный руководитель:

кандидат физико-математических наук,

доцент

Ефремова М. И.

Оценка научного руководителя _________________________________________

Оценка за оформление ________________________________________________

Оценка за доклад на защите работы _____________________________________

Итоговая оценка _____________________________________________________

Подписи членов комиссии по защите ____________________________________

Мозырь 2016

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ. 3

КАРТЕРОВЫ И ГАЩЮЦЕВЫ ПОДГРУППЫ РАЗРЕШИМЫХ ГРУПП. 4

КЛАССЫ ФИТТИНГА.. 8

ИНЪЕКТОРЫ.. 16

ЗАКЛЮЧЕНИЕ. 25

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 26

ВВЕДЕНИЕ

КАРТЕРОВЫ И ГАЩЮЦЕВЫ ПОДГРУППЫ РАЗРЕШИМЫХ ГРУПП.

Лемма 1. Пусть X — класс Шунка характеристики π и пусть H — X –проектор группы G. Тогда N_G (H)/ H — π' – группа.

Доказательство. Если N_G(H)/H неявляется π' – группой, то существует простое число p ∈ π, которое делит порядок N_G (H)/ H. По теореме Силова в группе N_G (H)/ H имеется подгруппа K/H порядка p. Так как в Xимеется подгруппа порядка p,то K/H ∈ X и H не является X –проектором K, противоречие.

Лемма 2. Пусть X — класс Шунка. Тогда и только тогда в каждой разрешимой группе X – проектор самонормализуем, когда N⊆X.

Доказательство. Пусть в каждой разрешимой группе X–проектор совпадает со своим нормализатором. Предположим, что N не содержится в X. Тогда существует группа G ∈ N \ X. Пусть H — X–проектор группы G. Так как G ∉ X, то H ≠ G. Но в нильпотентных группах собственные подгруппы отличны от своих нормализаторов, поэтому N_G (H)≠ H,получили противоречие. Значит допущение неверно и N⊆X.

Обратно, пусть N⊆X и допустим, что существует разрешимая группа G, в которой X–проектор H — собственная подгруппа в своем нормализаторе. Пусть простое число p делит порядок N_G (H)/ H. Тогда в N_G (H)/ H существует подгруппа K/H порядка p. Так как K/H ∈ N⊆X,то H небудет X–проектором подгруппы K, противоречиe.

Картеровой подгруппой называют нильпотентную самонормализуемую подгруппу группы.

Теорема 3. В любой разрешимой группе множество N –проекторов совпадает с множеством картеровых подгрупп.

Доказательство. Пусть H — N–проектор группы G. Тогда H нильпотентна и по лемме 2 совпадает со своим нормализатором, т.е. H является картеровой подгруппой группы G.

Обратно, пусть H — картерова подгруппа группы G. Воспользуемся индукцией по порядку группы. Так как в нильпотентных группах собственные подгруппы отличны от своих нормализаторов, то H — N–максимальная подгруппа группы G. Cуществует нильпотентная нормальная подгруппа N группы G такая, что HN — собственная подгруппа. По индукции H — N–проектор группы HN. Пусть

xN ∈ N_{G / N} (HN / N).

Тогда H^x — картерова подгруппа группы (HN) ^x = HN и по индукции подгруппа

H^x — N–проектор группы HN. Поэтому подгруппы H и H^x сопряжены в HN, т.е.существует элемент y ∈ HN такой, что H^x = H^y. Теперь

xy⁻¹ ∈ N_G (H) = H, x ∈ Hy ⊆ HN.

Таким образом, HN/N — самонормализуемая нильпотентная подгруппа группы G/N. По индукции подгруппа

HN/N — N–проектор группы G/N и подгруппа H — N–проектор группы G.

Следствие 4. В любой разрешимой группе картеровы подгруппы существуют и сопряжены между собой.

Лемма 5. Если в примитивной разрешимой группе G примитиватор имеет простой индекс, то группа G сверхразрешима.

Доказательство. Пусть G — примитивная группа, M — её примитиватор и | G: M | = p — простое число. Пусть N ·⨞ G. По теореме, группа G = [ N ] M и N = C_G (N). Теперь | N | = p и G / N изоморфна группе автоморфизмов группы N, которая является циклической группой порядка, делящего p −1. Поэтому M циклическая и группа G сверхразрешима.

Гащюцевой подгруппой группы G называется подгруппа H группы G, удовлетворяющая следующим двум требованиям:

(1) H сверхразрешима;

(2) если H ≤ H₁ < T ≤ G, то| T: H₁ | — непростое число.

Теорема 6. В любой разрешимой группе множество U –проекторов совпадает с множеством гащюцевых подгрупп.

Доказательство. Пусть H — U–проектор разрешимой группы G. Тогда H сверхразрешима. Предположим, что существуют подгруппы H₁ и T такие, что

H ≤ H₁ <· T, | T: H₁ | = p

— простое число. Тогда T / Core_T (H₁) — примитивная группа с примитиватором H₁ / Core_T (H₁) индекса p в T / Core_T (H₁). По лемме 5 группа T / Core_T (H₁) сверхразрешима.Так как H — U–проектор T, то

T = HCore_T (H₁) = H₁,

противоречие. Поэтому допущение неверно и если H ≤ H₁ < · T, то | T: H₁ | — не простое число.

Обратно, пусть выполняются требования (1) и (2) из определения гащюцевой подгруппы. Если H < · T и T ∈ U, то | T: H | — простое число, что противоречит (2). Поэтому H — U–максимальная подгруппа группы G. Cуществует нильпотентная нормальная неединичная подгруппа N группы G такая, что HN — собственная подгруппа. Рассмотрим факторгруппу G / N. Ясно,что HN / N сверхразрешима. Если

HN / N ≤ H₁ / N < · T / N ≤ G / N,

то

H ≤ H₁ < · T ≤ G

И | T: H₁ | не простое число.Таким образом, HN / N — гащюцева подгруппа фактор группы G / N. По индукции HN / N является U–проектором факторгруппы G / N и подгруппа H — U–проекторгруппы G.

Следствие 7. В любой разрешимой группе гащюцевы подгруппы существуют и сопряжены между собой.

Теорема 8. В любой разрешимой группе множество Sπ–проекторов совпадает со множеством π–холловых подгрупп.

Доказательство. Воспользуемся индукцией по порядку группы. Класс S_π всех разрешимых π–групп является насыщенной формацией, поэтому S_π–проекторы существуют и сопряжены в каждой разрешимой группе. Пусть H — S_π –проектор разрешимой группы G и пусть N — минимальная нормальная подгруппа группы G. Тогда H — π –подгруппа группы G. Так как HN / N — S_π –проектор группы G / N, то по индукции HN / N — π –холлова подгруппа группы G / N. Если HN ≠ G, то по индукции H — π –холлова подгруппа группы HN, поэтому из равенства

| G: H |=| G: HN || HN: H |

следует, что H — π –холлова подгруппа группы G. Если HN = G, то H — максимальная подгруппа группы G и H ∩ N = E. Если N — p –группа для p ∈ π, то G — π –группаи G = H ∈ S_π. Если p ∈ π, то | G: H | = | N | — π' –число и H — π –холлова подгруппа группы G. Итак, каждый S_π–проектор разрешимой группы G является π –холловой подгруппой группы G. Обратно, пусть H — π –холлова подгруппа группы G. Тогда H — S_π–проектор группы G.

Следствие 9. Для произвольного множества π простых чисел в каждой разрешимой группе Gπ –холловы подгруппы существуют и сопряженны между собой.

КЛАССЫ ФИТТИНГА

Класс X называется нормально наследственным или классом, замкнутым относительно нормальных подгрупп, если выполняется следующее требование:

(1) Если G ∈ X и N /G, то N ∈ X.

Очевидно, что если класс X замкнут относительно нормальных подгрупп, то X замкнут относительно субнормальных подгрупп, т.е. если G ∈ X и N ⨞⨞ G, то N ∈ X.

Класс X называется замкнутым относительно произведений нормальных X–подгрупп, если выполняется следующее требование:

(2) если N₁ и N₂ ⨞ G, N₁ и N₂ ∈ X, то N₁N₂ ∈ X.

Классом Фиттинга называется класс X, замкнутый относительно нормальных подгрупп и произведений нормальных X–подгрупп. Класс Фиттинга называют также радикальным классом.

Пример 1. Классы S, N, S_π, N_π для любого множества простых чисел π являются классами Фиттинга.

Действительно, для указанных классов выполняются требования (1) и (2) из определения класса Фиттинга.

Пример 2. Для каждого натурального k класс N^k всех разрешимых групп нильпотентной длины ≤ k будет классом Фиттинга.

Пример 3. Классы A и U не являются классами Фиттинга.

Действительно, для классов A и U требование (1) выполняется, а требование (2) нарушается. Например, неабелева диэдральная подгруппа D₈ порядка 8 является произведением двух абелевых подгрупп A и B порядка 4. Поэтому D₈ = AB ∉ A, но A и B ∈ A. Для класса сверхразрешимых групп U.

Теорема 4. Если класс X замкнут относительно произведений нормальных X –подгрупп, то каждая субнормальная X –подгруппа группы G содержится в некоторой нормальной X –подгруппе группы G.

Доказательство. Пусть H — субнормальная X–подгруппа группы G. Применим индукцию по индексу | G: H |. Заметим, что H ≠ N_G (H) и N_G (H) ≠ G. Выберем подгруппу L в группе G, обладающую следующим свойством: подгруппа L порождается всеми субнормальными подгруппами X группы G такими, что H ≤ X ≤ N_G (H).

Ясно, что H ≤ L ≤ N_G (H). Так как по теореме, подгруппа, порожденная субнормальными подгруппами, является субнормальной подгруппой, то L субнормальна и существует субнормальная подгруппа M в группе G такая, что L ⨞ M и M ≠ L. По выбору L подгруппа M не содержится в N_G (H). Поэтому существует элемент x ∈ M \ N_G(H). Ясно,что

H ≠ H^x, H^x ∈ X

и H^x — субнормальная подгруппа группы G. Поскольку H ⨞ L, то H^x ⨞ L^x = L. Теперь HH^x — подгруппа группы L и HH^x ∈ X по требованию (2). Кроме того, HH^x ≠ H, поэтому к подгруппе HH^x применима индукция. По индукции существует нормальная подгруппа N в группе G такая, что N ∈ X и HH^x ≤ N. Теперь H ≤ N.

Следствие 5. Пусть класс X замкнут относительно произведений нормальных X –подгрупп. Если H₁ и H₂ — субнормальные X –подгруппы группы G, то ⟨ H1, H2 ⟩ — субнормальная X–подгруппа.

Доказательство. Пусть M = ⟨ H₁, H₂ ⟩. По теореме 4 существуют в группе M нормальные X–подгруппы N₁ и N₂ такие, что H₁ ≤ N₁, H₂ ≤ N₂. По требованию (2) произведение N₁N₂ ∈ X. Поэтому

M = ⟨ H₁, H₂ ⟩ ≤ N₁N₂ ≤ M

и M = N₁N₂ ∈ X.

Следствие 6. Пусть класс X замкнут относительно произведений нормальных X –подгрупп. Если H — субнормальная X –подгруппа группы G, то H^G ∈X.

Доказательство. Подгруппа H ^G порождается всеми сопряженными с H подгруппами группы G, т.е.

H^G = ⟨ H^g | g ∈ G ⟩.

По следствию 5 получаем, что H^G ∈ X.

Применяя следствие 6 к классам всех разрешимых инильпотентных групп, получаем

Следствие 7. Пусть H — субнормальная подгруппа группы G. Тогда:

(1) если H — разрешимая подгруппа, то H^G разрешима;

(2) если H — нильпотентная подгруппа, то H^G нильпотентна.

Заметим, что для классов X требование (2) эквивалентно требованию

(3) если N₁ и N₂ ⨞⨞ G, N₁ и N₂ ∈ X, то ⟨ N ₁, N ₂⟩ ∈ X.

Пусть X — класс Фиттинга. Произведение всех нормальных X –подгрупп группы G называется X – радикалом группы G и обозначается через G _X. Таким образом,

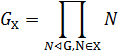
Ясно, что X–радикал G _X является наибольшей нормальной подгруппой группы G, содержащейся в X.

Пример 8. Если G — группа, то N–радикал G _N совпадает с подгруппой Фиттинга F (G) группы G.

Лемма 9. Пусть X — класс Фиттинга, G — группа и H ⨞⨞ G. Тогда и только тогда H ∈ X, когда H ≤ G _X.

Доказательство. Пусть H ⨞⨞ G и H ∈ X. По следствию 5 получаем, что H ≤ H^G ∈X и H^G ≤ G _X.

Обратно, пусть H ⨞⨞ G и H ≤ G _X. Так как G _X ∈ X и выполняется требование (1), то H ∈ X.

Лемма 10. Если X — класс Фиттинга и N ⨞⨞ G, то N _X = G _X ∩ N.

Доказательство. Так как

G _X ∩ N ⨞⨞ G _X

и G _X ∈ X, то G _X ∩ N ∈ X. Поскольку G _X ∩ N ⨞ N, то

G _X ∩ N ⊆ N _X.

Обратно,

N _X ⨞ N ⨞⨞ G,

поэтому N _X ⨞⨞ G и по лемме 9 подгруппа N _X ⊆ GX.

Итак

G _X ∩ N = N _X.

Лемма 11. Пусть группа G содержит нормальную подгруппу N индекса p, где p—простое число. Если Z—циклическая группа порядка p, то прямое произведение G×Z содержит нормальную подгруппу K, изоморфную G, и отличную от G.

Доказательство. Так как

(G × Z)/ N ≃ ,

Где — элементарная абелева группа порядка p², то в (G × Z)/ N существует (p² −1) элементов порядка p, которые распадаются на

(p² −1)/(p −1)=(p +1)

подгрупп порядка p. Поэтому существует в (G × Z)/ N подгруппа K / N порядка p такая, что

K / N ≠ G / N и Z ∉ K.

Подгруппа K нормальна в группе G × Z, K ≠ G. Кроме того, G × Z = K × Z и

(G × Z)/ Z ≃ G ≃ (K × Z / Z) ≃ K.

Теорема 12. Если класс Фиттинга X содержит разрешимую группу G, то N _{π ( G )}⊆ X.

Доказательство. Пусть G ∈ X ∩ S и p ∈ π (G). У разрешимой группы факторы композиционного ряда имеют простые порядки. Поэтому существуют подгруппы N ⨞ H ⨞⨞ G такие, что | H / N | = p. Пусть Z — циклическая группа порядка ⨞ p. По лемме 11 существует группа K, изоморфная H такая, что K / H × Z, K ≠ H. Теперь

HK = H × Z ∈ X.

Итак, класс X содержит группу порядка p.

Пусть P — произвольная p –группа. По индукции можно считать, что все собственные подгруппы группы P содержатся в X. Если в группе P имеются две различные подгруппы P ₁ и P ₂ индекса p, то P ₁ и P ₂ ∈ X по индукции, а так как для X выполняется требование (2), то P = P ₁ P ₂ ∈ X. Пусть в P только одна подгруппа индекса p. В этом случае группа P циклическая. Пусть | P | = pⁿ, | P ₁| = p^{n −1}. Построим группу

B = A ₁ ×... × A _p, A_i ≃ P ₁.

Пусть A_i = ⟨ a_i ⟩. Рассмотрим отображение γ: B → B такое, что

γ (a_i) = a_i +1, i =1,..., p −1, γ (a_p) = a ₁.

Легко проверить, что γ ∈ AutB, | γ | = p. Поэтому существует группа

M = ⟨ a ₁,..., a_p, γ ⟩ = B ×⟨γ⟩.

Теперь | M | = p ^{( n −1) p +1}, значит все подгруппы в M субнормальны. Так как B ∈ X и ⟨γ⟩ ∈ X, то M ∈ X. Вычислим порядок элемента a ₁ γ. Так как

(a ₁ γ) ^p = a ₁ γa ₁ γ... a ₁ γ = a ₁(γa ₁ γ ⁻¹)(γ ² a ₁γ⁻²)...(γ^{p −1} a ₁ γ ^1−p) = a ₁ a ₂... a_p

и a ₁ a ₂... a_p имеет порядок p^{n −1}, то элемент a ₁ γ имеет порядок pⁿ. Таким образом, P ∈ X. Итак, N_p ⊆ X для всех p ∈ π (G). Поэтому N _{π ( G )} ⊆ X.

Следствие 13. Если X — класс Фиттинга, то

X ∩ N = N_χ(X).

Доказательство. По теореме 12 имеем включение N _p ⊆ X для всех p ∈ χ (X). Поэтому

N _{χ (X)} ⊆ X ∩ N.

Обратно, если G ∈ X ∩ N, то N _{π ( G )} ⊆ X по теореме 12. Поэтому

π (G) ⊆ χ (X) и G ∈ N _{χ (X)}.

Итак, N ∩ X = N _{χ (X)}.

Следствие 14. Если X — класс Фиттинга, то

Доказательство. Пусть

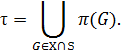
Если p ∈ χ (X), то существует группа Z_p простого порядка, принадлежащая X. Так как Z_p ∈ X ∩ S, то p ∈ τ. Обратно, если p ∈ τ, то существует разрешимая группа G ∈ X такая, что p ∈ π (G). По теореме 12 получаем, что N _{π ( G )} ⊆ X и p ∈ χ (X). Итак, χ (X) = τ

.

Пусть X — класс Фиттинга и Y—класс групп. Радикальным произведением X и Y называется класс

X⟐Y = { G ∈ E| G / G _X ∈ Y}.

Теорема 15. Если X и Y — классы Фиттинга, то X ⟐ Y — класс Фиттинга и X ⊆ X ⟐ Y.

Доказательство. Пусть G ∈ X ⟐ Y и H ⨞ G. Тогда H _X = H ∩ G _X и

H / H _X ≃ HG _X/ G _X ⨞ G / G _X.

Так как G / G _X ∈ Y и Y — класс Фиттинга, то H / H _X ∈ Y и H ∈ X ⟐ Y.

Пусть H_i ∈ X ⟐ Y, H_i ⨞ G, i = 1,2, и G = H ₁ H ₂. Тогда

H_iG _X/ G _X ≃ H_i / H_i ∩ G _X = H_i /(H_i)_X ∈ Y

и

G / G _X = H ₁ H ₂/ G _X = (H ₁ G _X/ G _X)(H ₂ G _X/ G _X) ∈ Y.

Поэтому G ∈ X ⟐ Y и X ⟐ Y — класс Фиттинга.

Если G ∈ X, то G = G _X и G / G _X = E ∈ Y, т.е. G ∈ X ⟐ Y. Таким образом, X ⊆ X ⟐ Y.

Теорема 16. Пусть X, Y и Z — классы Фиттинга. Тогда

(1) (G/G _X) _Y = G _X⟐Y/ G _X;

(2) (X⟐Y) ⟐Z = X⟐(Y⟐Z).

Доказательство. (1) По теореме 15 произведение X ⟐ Y — класс Фиттинга и X ⊆ X⟐Y. Поэтому G _X ⊆ G _X⟐Y, а так как G _X⟐Y ∈ X ⟐ Y, то G _X⟐Y/ G _X ∈ Y. Отсюда следует, что

G _X⟐Y/ G _X ⊆ (G / G _X)_Y.

Проверим обратное включение. Обозначим

(G / G _X)_Y = H / G _X.

Так как H ⨞ G, то H _X ⊆ G _X, поэтому H _X = G _X. Но H / G _X ∈ Y, значит H ∈ X ⟐ Y, т.е.

H / G _X ⊆ G _X⟐Y / G _X.

Таким образом,

(G / G _X)_Y = (G _X⟐Y)/ G _X.

(2) Пусть

G ∈ (X⟐Y)⟐Z.

Это означает, что G / G _X⟐Y ∈ Z. Но

G / G _X⟐Y ≃ (G / G _X)/(G _X⟐Y/ G _X) = (G / G _X)/(G / G _X)_Y.

Из того,что

(G / G _X)/(G / G _X)_Y ∈ Z

следует, что

G / G _X ∈ Y ⟐ Z, G ∈ X ⟐ (Y ⟐ Z).

Аналогично проверяется, что

X ⟐ (Y ⟐ Z) ⊆ (X ⟐ Y) ⟐ Z.

Пусть X и Y — произвольные классы групп. Через Ext _XY обозначим совокупность всех групп, в которых имеется нормальная X-подгруппа и фактор группа по ней принадлежит Y,т.е.

Ext _XY = { G ∈ E| ∃ N ⨞ G, N ∈ X, G / N ∈ Y}.

Теорема 17. Если X — класс групп, замкнутый относительно нормальных подгрупп, и Y — формация, то X◦Y = Ext _XY.

Доказательство. По определению корадикального произведения имеем

X◦Y = { G ∈ E | G ^Y ∈ X}.

Поэтому ясно, что X◦Y ⊆ Ext _XY.

Обратно, пусть G ∈ Ext _XY. Тогда существует нормальная подгруппа N ∈ X, для которой G / N ∈ Y. Поскольку Y — формация, то G ^Y ⊆ N, а так как X замкнут относительно нормальных подгрупп, то G ^Y ∈ X и G ∈ X◦Y.

Теорема 18. Если X — класс Фиттинга и Y — гомоморф, то X ⟐ Y = Ext _XY.

Доказательство. По определению радикального произведения имеем

X ⟐ Y = { G ∈ E | G / G _X ∈ Y}.

Поэтому ясно, что X ⟐ Y ⊆ Ext _XY.

Обратно, пусть G ∈ Ext _XY. Тогда существует нормальная подгруппа N ∈ X такая, что G / N ∈ Y. Так как X — класс Фиттинга, то N ⊆ G _X. Теперь

G / G _X ≃ (G / N)/(G _X/ N),

а поскольку Y — гомоморф и G / N ∈ Y, то G / G _X ∈ Y и G ∈ X ⟐ Y.

Следствие 19. Если X — класс Фиттинга, а Y — формация, то X⟐Y=X◦Y = Ext _XY.

Следствие 20. Если X и Y — радикальные формации, то X ⟐ Y = X◦Y = Ext _XY.

ИНЪЕКТОРЫ

Пусть X — класс групп. Подгруппа H группы G называется X–инъектором, если для каждой субнормальной подгруппы K группы G пересечение H ∩ K является X– максимальной подгруппой в K.

Лемма 1. Пусть X — класс групп. Если H — X – инъектор группы G и K ⨞⨞ G, то H ∩ K — X –инъектор подгруппы K.

Доказательство. Пусть N ⨞⨞ K. Тогда N ⨞⨞ G и

(H ∩ K) ∩ N = H ∩ N

X–максимальна в N. Это означает, что H ∩ K — X–инъектор подгруппы K.

Лемма 2. Пусть X — класс групп. Подгруппа H является X –инъектором группы G тогда и только тогда, когда H X –максимальна в G и H ∩ K — X – инъектор подгруппы K для всех максимальных нормальных подгрупп K группы G.

Доказательство. Пусть H — X–инъектор группы G. Тогда H X–максимальна в G и по лемме 1 подгруппа H ∩ K — X–инъектор подгруппы K.

Обратно, пусть H — X–максимальная подгруппа группы G и H ∩ K — X–инъектор подгруппы K для всех максимальных нормальных подгрупп K группы G. Пусть N ⨞⨞ G и ≤ L, L —максимальная нормальная подгруппа группы G. Так как H ∩ L — X–инъектор подгруппы L, то

H ∩ L ∩ N = H ∩ N

X–максимальна в N и H — X–инъектор группы G.

Теорема 3. Пусть X —класс группи Y — класс Фиттинга. Если в каждой Y –группе существует X –инъектор, то X ∩ Y — класс Фиттинга.

Доказательство. Пусть

G ∈ X ∩ Y, N ⨞⨞ G.

Тогда группа G является своим X–инъектором. Из определения X–инъектора получаем, что G ∩ N = N — X– максимальная подгруппа группы N для всех N ⨞⨞ G. Поэтому N ∈ X, а так как Y — класс Фиттинга, то N ∈ X ∩ Y и первое требование определения класса Фиттинга для X ∩ Y выполняется.

Пусть

N ₁, N ₂ ⨞ G, N ₁, N ₂ ∈ X ∩ Y.

Тогда N ₁ N ₂ ∈ Y поскольку Y — класс Фиттинга. По условию в группе N ₁ N ₂ существует X–инъектор, который обозначим через H. По определению X–инъектора подгруппа N_i ∩ H X–максимальна в N_i, поэтому N_i ∩ H = N_i

и

N ₁ N ₂ = H ∈ X ∩ Y.

Значит для X ∩ Y выполняется и второе требование определения класса Фиттинга.

Следствие 4. (1) Пусть X — класс групп. Если в каждой группе существует X –инъектор, то X — класс Фиттинга.

(2) Разрешимый класс X, для которого каждая разрешимая группа обладает X –инъектором, является классом Фиттинга.

Доказательство. (1) Утверждение следует из теоремы в случае, когда Y — класс всех групп.

(2) Утверждение следует из теоремы в случае, когда Y = S — класс всех разрешимых групп.

Лемма 5. Пусть X — класс Фиттинга и H — X –максимальная подгруппа группы G. Если L — подгруппа группы G такая, что

H ≤ L ≤ N_G (H),

то N_G (L)≤ N_G (H). В частности, нормализатор X –максимальной подгруппы группы G самонормализуем.

Доказательство. Если x ∈ N_G (L), то H^x ⨞ L^x = L и HH^x ∈ X. Поскольку H X–максимальна, то H = H^x и x ∈ N_G (H).

Лемма 6. Пусть X — класс Фиттинга, G — разрешимая группа, N—нормальная подгруппа группы G с абелевой фактор группой G/N. Пусть W — X – максимальная подгруппа из N и пусть V₁ и V₂ — X – максимальные подгруппы группы G, содержащие W. Тогда V₁ и V₂ сопряжены в G.

Доказательство. Воспользуемся индукцией по порядку группы. Так как N ∩ V_i ∈ X, то

W = N ∩ V_i и V_i ≤ N_G (W)

для каждого i = 1,2. Если N_G (W) ≠ G, то по индукции подгруппы V ₁ и V ₂ сопряжены в N_G (W) и лемма справедлива. Поэтому следует считать, что подгруппа W нормальна в G. Пусть C_i / W — картерова подгруппа из

M_i / W = N_{G / W} (V_i / W) = N_G (V_i)/ W.

По условию леммы факторгруппа G / N абелева. Значит

G ' = [ G, G ] ≤ N и [ V_i, M_i ] ≤ N ∩ V_i = W.

Отсюда заключаем, что подгруппа V_i / W содержится в центре M_i / W. Но C_i / W самонормализуема в Mi / W, поэтому V_i ≤ C_i. По лемме 5 нормализатор N_G (C_i) ≤ M_i, поэтому

N_G (C_i)/ W = N_Mi (C_i)/ W = N_Mi / W (C_i / W) = C_i / W

и C_i / W — подгруппа Картера группы G / W. Следовательно, = C ₂ для некоторого элемента x ∈ G. Теперь и V ₂ — нормальные X–подгруппы из C ₂, поэтому

V ₂ ∈ X, = V ₂.

Теорема 7. Если X — класс Фиттинга, то в каждой разрешимой группе G существует X –инъектор и любые два X –инъектора группы G сопряжены.

Доказательство. Воспользуемся индукцией по порядку группы G. Так как группу G можно считать неединичной, то её коммутант G ' по индукции имеет X–инъектор, который обозначим через W. Через V обозначим X– максимальную подгруппу группы G, содержащую W. Пусть M — максимальная нормальная подгруппа группы G. Ясно, что G ' ≤ M. По индукции подгруппа M содержит X–инъектор U. По лемме 1 подгруппа U ∩ G ' — X–инъектор подгруппы G '. По индукции U ∩ G ' = W^x для некоторого x ∈ G '. Пусть T — X–максимальная подгруппа группы G, содержащая U. Теперь U ≤ T ∩ M ∈ X, поэтому U = T ∩ M. Подгруппы T и V^x содержат X– максимальную подгруппу W^x коммутанта G '. По лемме 6 они сопряжены, т.е. T^y = V^x для некоторого y ∈ G. Теперь

U^y = (T ∩ M) ^y = T^y ∩ M = V^x ∩ M.

Следовательно, V^x ∩ M — X–инъектор G по лемме 2. Итак, существование X–инъектора в группе G доказано.

Пусть V ₁ и V ₂ — X–инъекторы группы G. Тогда V ₁ ∩ G ' и V ₂ ∩ G ' — X–инъекторы подгруппы G '. По индукции

V ₁ ∩ G ' = (V ₂ ∩ G ')^g

для некоторого g ∈ G '. Применяя лемму 6 для подгрупп W = V ₁ ∩ G ' ≤ V ₁ ∩ , получаем, что V ₁ и V ₂ сопряжены в группе G.

Теорема 8. Пусть X — класс Фиттинга и G — разрешимая группа. Подгруппа H тогда и только тогда является X –инъектором группы G, когда H X –максимальна в G и H ∩ G ' — X –инъектор коммутанта G'.

Доказательство. Если H — X–инъектор группы G, то H X–максимальна в группе G и H ∩ G ' — X–инъектор подгруппы G ' по лемме 1. Пусть H — X–максимальная подгруппа группы G и H ∩ G ' — X–инъектор в G '. Пусть K — X–инъектор группы G, он существует по теореме 7. По лемме 1 пересечение K ∩ G ' — X–инъектор подгруппы G '. По теореме 7 подгруппы K ∩ G ' и H ∩ G ' сопряжены между собой, т.е. существует элемент g ∈ G ' такой, что

H ∩ G ' = (K ∩ G ')^g = K^g ∩ G '.

Теперь подгруппы H и K^g X–максимальны в G и содержат X–максимальную подгруппу K^g ∩ G '. По лемме 6 подгруппы H и K^g сопряжены, поэтому H — X–инъектор группы G.

Следствие 9. Пусть X — класс Фиттинга и пусть

E = G_n ⨞ G_n−1 ⨞ ... ⨞ G₁ ⨞ G₀ = G

—ряд с абелевыми факторами G_i/G_i+1. Подгруппа H тогда и только тогда является X –инъектором группы G, когда H ∩ G_i является X –максимальной подгруппой в G_i для всех i.

Доказательство. Если H — X–инъектор группы G, то H ∩ G_i — X–инъектор подгруппы G_i по лемме 1, поэтому H ∩ G_i является X–максимальной подгруппой в G_i для всех i.

Обратно, пусть H ∩ G_i является X–максимальной подгруппой в G_i для всех i. По индукции H ∩ G ₁ — X– инъектор в G ₁. Так как G / G ₁ абелева, то G ' ≤ G ₁ и подгруппа H — X–инъектор группы G по теореме 8.

Следствие 10. Пусть X — класс Фиттинга и G — разрешимая группа. Подгруппа H тогда и только тогда является X –инъектором группы G, когда для любой нормальной подгруппы N группы G пересечение H ∩ N является X –максимальной подгруппой в N.

Доказательство. Если H — X–инъектор группы G, то из определения X–инъектора следует, что пересечение H ∩ N X–максимальна в N для всех нормальных подгрупп N группы G.

Обратно, пусть для любой нормальной подгруппы N группы G пересечение H ∩ N является X–максимальной подгруппой в N. Тогда, в частности, H ∩ G ^{( i )} —X–максимальная подгруппа в G ^{( i )} для всех i, где G ^{( i )} — i –й коммутант группы G. Теперь для разрешимой группы G и её производного ряда

E = G ^{( n )}⨞ G ^{( n −1)}⨞... ⨞G'⨞G

выполняются условия следствия 9, поэтому подгруппа H X–инъектор в G.

Следствие 11. Пусть X — класс Фиттинга и G — разрешимая группа. Если H — X –инъектор группы G и H ≤ K ≤ G, то H — X –инъектор в K.

Доказательство. Пусть

E = G_n ⨞ G_{n −1}⨞...⨞ G ₁⨞ G ₀ = G

— ряд с абелевыми факторами G_i / G_{i +1} и K_i = K ∩ G_i. Тогда ряд

E = K_n ⨞ K_{n −1}⨞...⨞ K ₁⨞ K ₀ = K

имеет абелевы факторы K_i / K_{i +1}. Кроме того,

H ∩ G_i ≤ K ∩ G_i ≤ G_i

и H ∩ G_i X–максимальна в G_i. Поэтому

H ∩ G_i = H ∩ (K ∩ G_i) = H ∩ K_i

X–максимальна в K ∩ G_i = K_i. Применяя следствие 9 получаем, что H — X–инъектор в K.

Теорема 12. Пусть X — класс Фиттинга и G — нильпотентная группа. Подгруппа H группы G X –максимальна тогда и только тогда, когда H — χ (X) холлова подгруппа.

Доказательство. Пусть H — X–максимальная подгруппа группы G. Так как

H ∈ X ∩ N = N _{χ (X)},

то H будет χ (X) – подгруппой. Если K — χ (X)-холлова подгруппа, то

H ≤ K ∈ N _{χ (X)} = X ∩ N

и K — X-подгруппа. Поэтому H = K.

Обратно, если H — χ (X)–холлова подгруппа группы G, то H ∈ N _{χ (X)} = X ∩ N. Если K X–максимальна в G и K ≥ H, то

K ∈ X ∩ N = N _{χ (X)}

и K — χ (X)–подгруппа. Поэтому H = K.

Следствие 13. Пусть X — класс Фиттинга и G — нильпотентная группа. Подгруппа H группы G является X –инъектором тогда и только тогда, когда H —χ (X) -холлова подгруппа.

Теорема 14. Пусть X —класс Фиттинга и G — группа с нильпотентным коммутантом G '. Подгруппа H тогда и только тогда является X –инъектором группы G, когда H X –максимальна в G и содержит χ (X) –холлову подгруппу из G '.

Доказательство. Пусть H — X–инъектор группы G. Тогда H X–максимальна в группе G и H ∩ G ' — X–инъектор подгруппы G '. Так как подгруппа G ' по условию нильпотентна, то

H ∩ G ' = G ' _{χ (X)}

— χ (X)–холлова подгруппа в G ' по следствию 13.

Обратно, пусть H X–максимальная подгруппа группы G и H содержит χ (X)–холлову подгруппу группы G '. Пусть K X–инъектор группы G, он существует по теореме 7. Тогда по лемме 1 пересечение K ∩ G ' — X–инъектор подгруппы G '. По следствию 13 пересечение

K ∩ G ' = G ' _{χ (X)}

является χ (X)–холловой подгруппой. Теперь K и H сопряжены по лемме 6. Значит H — X–инъектор группы G.

Следствие 15. Пусть X — класс Фиттинга и G — сверхразрешимая группа. Подгруппа H тогда и только тогда является X –инъектором группы G, когда H X –максимальна в группе G и содержит χ (X) – холлову подгруппу коммутанта.

Пример 16. В группе S ₃× Z ₂ подгруппа H = Z ₃× Z ₂ является N–инъектором, где Z ₃ — силовская 3–подгруппа из S ₃. Но H не является холловой подгруппой.

Пусть X — класс групп. Подгруппа H группы G называется X–биектором, если H ∩ N X-максимальна в N, а HN / N X-максимальна в G / N для каждой нормальной подгруппы N. Ясно, что X–биектор одновременно является X–проектором и X–инъектором группы G. Примерами X–биекторов служат силовские p –подгруппы групп для класса X = N _p всех p –групп.

Пример 17. В группе S ₄ силовская 2–подгруппа является N –биектором.

Для класса Шунка F каждая разрешимая группа G обладает единственным классом сопряженных F проекторов. Если F — радикальный класс, т.е. класс Фиттинга, то каждая разрешимая группа содержит единственный класс сопряженных F-инъекторов. Но наиболее употребительные классы групп являются одновременно и классами Шунка и радикальными классами. Поэтому вполне естественно возникает вопрос о существовании F–биекторов в разрешимых группах для радикального класса Шунка F.

Теорема 18. Пусть F — радикальный класс Шунка. Тогда в каждой нильпотентной группе G существует F –биектор H и подгруппа H является χ (F) –холловой подгруппой.

Доказательство. Утверждение вытекает из следствия 13.

Следствие 19. Пусть F —радикальная насыщенная формация. Тогда в каждой нильпотентной группе G существует F –биектор H и подгруппа H является χ (F) –холловой подгруппой.

Обозначим через Proj _F(G) совокупность всех F– проекторов группы G, а через Inj _F(G) совокупность всех F–инъекторов.

Теорема 20. Пусть F — радикальный класс Шунка. Если в метанильпотентной группе G существует F –биектор H, то H является χ (F) –холловой подгруппой группы G.

Доказательство. Пусть

H ∈ Inj F(G) ∩ Proj _F(G).

Так как в разрешимой группе все F–проекторы и все F– инъекторы сопряжены между собой, то

Inj _F(G) = Proj _F(G).

Пусть K = F (G) — подгруппа Фиттинга. Так как K ∩ H — F–инъектор в K, то по следствию 13 подгруппа K ∩ H является χ (F)–холловой подгруппой в K. Так как G / K нильпотентна и HK / K является F–проектром в G / K, то HK / K будет χ (F)–холловой подгруппой в G / K. Поскольку

HK / K ≃ H /(H ∩ K),

то H — χ (F)–подгруппа. Кроме того,

| G: H | = | K: (H ∩ K)||(G / K): (HK / K)|

и | G: H | есть χ (F) '–число. Значит, H — χ (F)–холлова подгруппа.

Следствие 21. Пусть F — радикальная насыщенная формация. Если в метанильпотентной группе G cуществует F –биектор H, то H является χ (F) –холловой подгруппой.

Пример 22. Группа S ₄× Z ₃ не является метанильпотентной, но N –проекторы и N –инъекторы совпадают между собой и являются нехолловыми подгруппами порядка 24.

Теорема 23. Пусть F — радикальный класс Шунка и M — нормально наследственный гомоморф, состоящий из разрешимых групп. Если в каждой группе G ∈ M существует F –биектор, то M _{χ (F)}⊆F.

Доказательство. Предположим, что M _{χ (F)} не содержится в F, и пусть G — группа наименьшего порядка из разности M _{χ (F)}\F. Если G имеет простой порядок p, то p ∈ χ (F) и G ∈N _p ⊆ F, противоречие. Значит, G — группа непростого порядка и можно выбрать нетривиальную нормальную в G подгруппу N. Так как N ∈ M и N — χ (F)–подгруппа в G, то N ∈ M _{χ (F)} и N ∈ F.

Пусть H — F–биектор в G. Тогда H — F–инъектор в G и N ≤ H. Поскольку H является F–проектором в G, то H / N F–максимальна в G / N. Так как M — гомоморф, то G / N ∈ M _{χ (F)}, а по выбору группы G получаем, что G / N ∈ F, т.е. H = G и G ∈ F, противоречие. Значит, допущение неверно и M _{χ (F)} ⊆ F.

Следствие 24. Если F —радикальный класс Шунка, для которого в каждой разрешимой группе существует F –биектор, то F = S _{χ (F)}.

Следствие 25. Если F — радикальная насыщенная формация, для которой в каждой разрешимой группе существует F –биектор, то F = S _{χ (F)}.

ЗАКЛЮЧЕНИЕ