
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула Тейлора для функции с остаточным членом в форме Пеано
|
|
Полностью таблица производных и правила дифференцирования


Определение предела функции
а) на «языке эпсилон-дельта»


б)

Определение производной
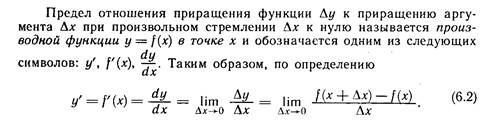
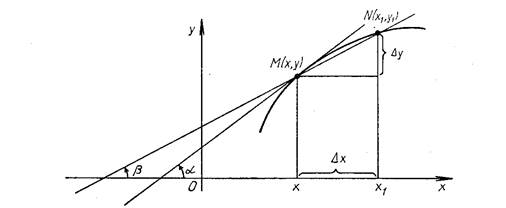
Таблица эквивалентных пар
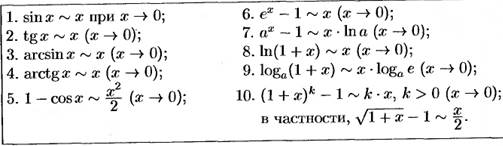
Уравнение касательной
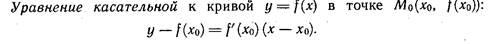
Формула для вычисления первой производной параметрической функции

Тогда производная функции y по переменной x равна:

Необходимые условия возрастания (убывания) дифференцируемой функции
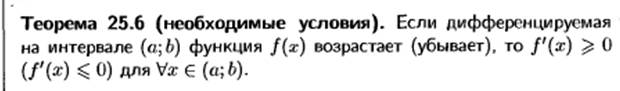
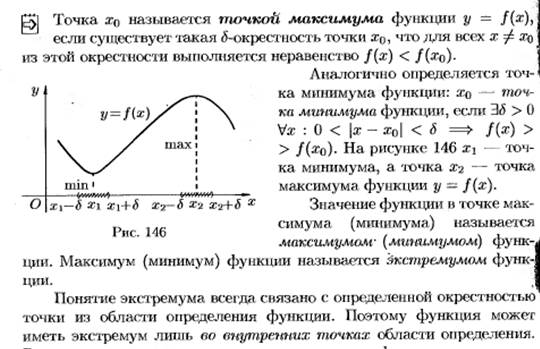
Определение максимума (минимума)
Необходимые условия экстремума дифференцируемой функции

Необходимые условия выпуклости вверх (вниз) дифференцируемой функции.
Если кривая y = f(x) на интервале (a;b) выпукла (вогнута), то вторая производная функции y = f(x) отрицательна (положительна) во всех точках интервала, т.е. f ²(x) <0 (f ²(x) >0).
Формула Тейлора для функции с остаточным членом в форме Пеано.
Если функция f n раз дифференцируема в точке x0 , то в некоторой окрестности этой точки

где 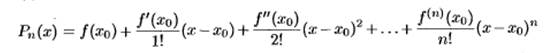
многочлен Тейлора порядка n для функции f в точке x = x0,
а Rn(x) = o((x-x0)n) – остаточный член формулы Тейлора в форме, данной Пеано, при x® x0.
| <== предыдущая | | | следующая ==> |
| Ты любила мои вещи, я писал их для тебя | | | Председатель районного совета Вересова Н.А |
Date: 2016-05-25; view: 2057; Нарушение авторских прав