
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методика решения нормальных уравнений
|
|
Один из возможных способов минимизации критерия аппроксимации (2) предполагает решение системы нормальных уравнений (3). При выборе в качестве аппроксимирующей функции линейной функции искомых параметров нормальные уравнения представляют собой систему линейных алгебраических уравнений.
Систему n линейных уравнений общего вида:

(4)
(4) можно записать посредством матричных обозначений в следующем виде: А·Х=В,
 ;
;  ;
; 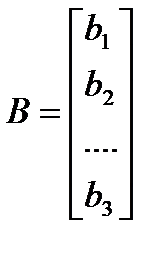 (5)
(5)
квадратная матрица А называется матрицей системы, а вектора Х и В соответственно вектором-столбцом неизвестных систем и вектором-столбцом ее свободных членов.
В матричном виде исходную систему n линейных уравнений можно записать и так:

(6)
Решение системы линейных уравнений сводиться к отысканию значений элементов вектора-столбца (хi), называемых корнями системы. Чтобы эта система имела единственное решение, входящее в нее n уравнение должно быть линейно независимым. Необходимым и достаточным условием этого является неравенство нулю определителя системы, т.е. Δ=detA≠0.
Алгоритм решения системы линейных уравнений подразделяется на прямые и итерационные. На практике никакой метод не может быть бесконечным. Для получения точного решения итерационные методы требуют бесконечного числа арифметических операций. Практически это число приходиться брать конечным и поэтому решение в принципе имеет некоторую ошибку, даже если пренебречь ошибками округлений, сопровождающими большинство вычислений. Что же касается прямых методов, то они даже при конечном числе операций могут в принципе дать точное решение, если оно существует.
Прямые и конечные методы позволяют найти решение системы уравнений за конечное число шагов. Это решение будет точным, если все промежутки вычисления проводятся с ограниченной точностью.
3. Ручной счёт.
Исходная функциональная зависимость представлена таблично, парами значения  и
и 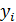 ..
..
Найти параметры 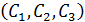 аппроксимирующей функции
аппроксимирующей функции  , пользуясь методом наименьших квадратов. Поиск параметром осуществить, используя методом Гаусса. Оценить погрешность аппроксимации посредством критерия качества
, пользуясь методом наименьших квадратов. Поиск параметром осуществить, используя методом Гаусса. Оценить погрешность аппроксимации посредством критерия качества  и максимального по модулю отклонения аппроксимирующей функции от исходной.
и максимального по модулю отклонения аппроксимирующей функции от исходной.
| Номер варианта | n | Значение  и и 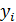
| Базисные функции | Метод решения СЛАУ | |||
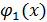
| 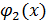
| 
| |||||
| X | 2,0 3,0 4,0 5,0 6,0 | 
| ln(
| x | Гаусса | ||
| Y | 2,41 2,85 3,91 -5,2 -9,8 |
1. Выражение для аппроксимации функции будет иметь следующий вид:

2. Запишем выражение для критерия аппроксимации
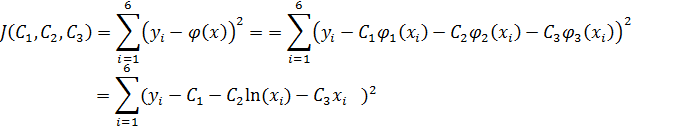
3. В соответствии с условиями локального минимума функции 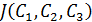 найдём частные производные
найдём частные производные  ,
,  ,
, 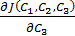 и приравняем их к нулю:
и приравняем их к нулю:
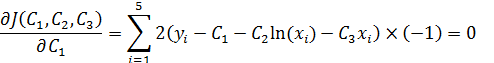


Таким образом, получим три уравнения
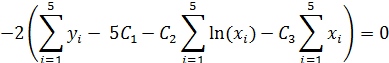
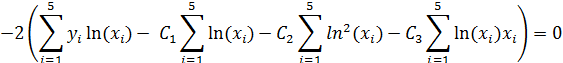

4. Приведём полученную систему уравнений к нормальному виду, перенеся свободные члены вправо и поделив обе части уравнения на 2.
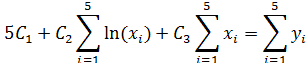
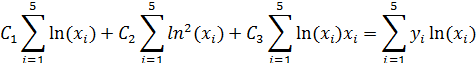
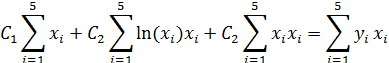
5. Для удобства представим промежуточные результаты вычислений в таблице

| 
| 
| 
| 
| 
| |
| 2,0 | 2,41 | 0,643 | 0,413 | 1,386 | ||
| 3,0 | 2,85 | 1,098 | 1,206 | 3,294 | ||
| 4,0 | 3,91 | 1,386 | 1,830 | 5,544 | ||
| 5,0 | -5,2 | 1,609 | 2,588 | 8,045 | ||
| 6,0 | -9,8 | 1,791 | 3,207 | 10,746 | ||
| Сумма | -5,83 | 6,527 | 9,244 | 29,015 |
Используя значение из таблицы, запишем систему уравнений в окончательном виде



Введя обозначения
 ;
;  ;
;  ;
;  ;
;
 ;
; 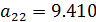 ;
;  ;
; 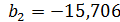 ;
;
 ;
; 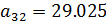 ;
; 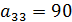 ;
;  ;
;
данную систему уравнений можно записать можно в матричном виде:

6. Полученную систему уравнений решим тем способом, который указан в задании.
1. Метод Гаусса
Множитель, на который необходимо умножать второе уравнение будет  , а множитель, на который необходимо умножат третье уравнение
, а множитель, на который необходимо умножат третье уравнение 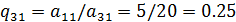
Если из первого уравнения вычесть второе, умноженное на 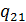 и третье умноженное на
и третье умноженное на  , то получим систему
, то получим систему
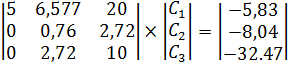
Множитель, на который необходимо умножать третье уравнение будет  .279
.279
Если из второго уравнения вычесть третье, умноженное на  , то получим систему:
, то получим систему:

Решение данной системы имеет вид:

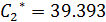

7. В результате решения исходной системы линейных уравнений и нахождения значений получаем запись искомой аппроксимирующей функции в следующем виде
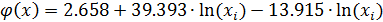
8. Оценка погрешности аппроксимации.
Рассчитаем значение аппроксимирующей функции в заданных точках  и соответствующее отклонение
и соответствующее отклонение 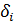 .
.
В соответствии с таблицей построим график исходной и аппроксимационной функции.

| 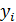
| 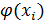
| 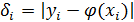
| |
| 2,0 | 2,41 | 2,133 | 0,277 | |
| 3,0 | 2,85 | 4,191 | 1,341 | |
| 4,0 | 3,91 | 1,609 | 2,301 | |
| 5,0 | -5,2 | -3,516 | 1,684 | |
| 6,0 | -9,8 | -10,248 | 0,448 |

Вычислим значение критерия аппроксимации:
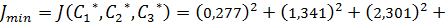
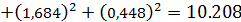
Максимальное по модулю отклонение  при
при 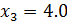
4. Текст программы и результат расчётов параметров на ЭВМ.
Схемы алгоритмов
Схема алгоритма основной программы:
| Начало |
| Вывод «Vector B:» |
i=0; i<n; i++
| Ввод x(i) |
i=0; i<n; i++
| Вывод Bi |
| Ввод y(i) |
i i
| metodgaussa(A[m][m],B[m],C[m]) |
| koeff(A[m][m],B[m],x[n],y[n]) |
| Вывод C1,C2,C3 |
| Вывод «Matrica A:» |
| Вывод F |
| res(X[n],Y[n],C[m],G[n]) |
| Вывод Aij |
| approk(G[n]) |
| оtkl(G[n],X[n]) |
j
| Конец |
i
koeff -схема алгоритма функции расчёта коэффициентов
| Начало |
i=0; i<m; i++
j=0; j<m; j++
| Sum=0 |
I=0; I<n; I++
| Sum=Sum + fi(i,x[I])*fi(j,x[I]) |
I
| A[i][j]=Sum |
j
| Sum=0 |
I=0; I<n; I++
| Sum=Sum + fi(i,x[I])*y[I] |
I
| B[i]=Sum |
i
| Конец |
vivodres - Схема алгоритма функции расчёта F[i], D[i]
| Начало |
i=0; i<n; i++
| F[i]=C[0]+C[1]*ln(x[i])+C[2]*(x[i])) |
| D[i]=Y[i]-F[i] |
| Вывод (x[i],y[i],F[i],D[i]) |
i
| Конец |
approk- cхема алгоритма функции расчёта и вывода Kr
| Начало |
| Kr=0 |
i=0; i<n; i++
| Kr=Kr+D[i]*D[i] |
i
| Конец |
| Вывод (Kr) |
otkl - подпрограммы поиска и вывода максимального отклонения по модулю
| Начало |
| g=|D[0]| |
| max=0 |
i=0; i<n; i++
| |D[i]| > g |
Да
| g=|D[i]| |
| max=i |
i
| Конец |
| Вывод (D) |
metodgaussa- главная функция метода
| Начало |
| 4 1 |
i=0; i<m-1; i++ j
| C[i]=(B[i]-Sum)/(A[i][i]) |
k=0; k<m; k++
| C[i]=A[k][i]/A[i][i] |
| Конец |
| A[k][i]=0 |
j=i+1; j<m; j++
| A[k][j]=A[k][j]-C[i]*A[i][j] |
j
| B[k]=B[k]-C[i]*B[i] |
k
i
i=m-1;i>=0;i--
| Sum=0 |
j=i+1;j<m;j++
| Sum=Sum+ A[i][j]*C[j] |
| 4 1 |
fi - схема алгоритма функции выбора функций
| Конец |
| Начало |
| k=1 |
| Возрат 1 |
| k=x |
| Возрат ln(x) |
| Возрат x |
4.2. Текст программы и результат расчётов параметров на ЭВМ
#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <cmath>
#define n 5
#define m 3
void koeff(float A[m][m], float B[m], float x[n], float y[n]);
float fi(float x, int k);
void metodgaussa(float A[m][m], float B[m], float C[m]);
void otkl(float G[n], float X[n]);
void approk(float G[n]);
void res(float X[n], float Y[n], float C[m], float G[n]);
int main()
{
int i, k, j;
float A[m][m], B[m], C[m], D[n], x[n], y[n];
printf("Vvedite X:\n");
for (i = 0; i<n; i++)
{
scanf_s("%f", &x[i]);
}
printf("Vvedite Y:\n");
for (i = 0; i<n; i++)
{
scanf_s("%f", &y[i]);
}
koeff(A, B, x, y);
printf("matrica A: ");
for (i = 0; i<m; i++)
{
printf("\n");
for (j = 0; j<m; j++)
printf("%9.4f ", A[i][j]);
}
printf("\nVektor B:\n");
for (i = 0; i<m; i++)
{
printf("%5.4f ", B[i]);
}
metodgaussa(A, B, C);
printf("\n");
printf("\nKoefficienti C1=%5.4f, C2=%5.4f, C3=%5.4f", C[0], C[1], C[2]);
printf("\n");
printf("\nF=%4.4f+%4.4f(x)+%4.4f(x*x)", C[0], C[1], C[2]);
printf("\n");
res(x, y, C, D);
printf("\n");
approk(D);
printf("\n");
otkl(D, x);
_getch();
}
float fi(float x, int k)
{
if (k == 0)
return (1);
else
if (k == 1)
return (log(x));
else
if (k == 2)
return (x);
}
void koeff(float A[m][m], float B[m], float x[n], float y[n])
{
int i, j, l;
float S;
for (i = 0; i<m; i++)
{
for (j = 0; j<m; j++)
{
S = 0;
for (l = 0; l<n; l++)
S = S + fi(x[l], i)*fi(x[l], j);
A[i][j] = S;
}
S = 0;
for (l = 0; l<n; l++)
S = S + y[l] * fi(x[l], i);
B[i] = S;
}
}
void res(float X[n], float Y[n], float C[m], float D[n])
{
int i;
float F[n];
printf("\nRezultati vichislenii:\n");
printf("i X[i] Y[i] F[i] D[i]\n");
for (i = 0; i<n; i++)
{
F[i] = C[0] + C[1] * (log(X[i])) + C[2] * (X[i]);
D[i] = Y[i] - F[i];
printf("%i %5.4f %5.4f %6.4f %6.4f\n", i + 1, X[i], Y[i], F[i], D[i]);
}
}
void approk(float D[n])
{
int i;
float Kr;
Kr = 0;
for (i = 0; i<n; i++)
Kr = Kr + D[i] * D[i];
printf("\nMin. znachenie kachestva approksimacii:");
printf("Kr=%7.6f ", Kr);
}
void otkl(float D[n], float X[n])
{
int i, max;
float g;
g = fabs(D[0]);
max = 0;
for (i = 1; i<n; i++)
if (fabs(D[i])>g)
{
g = fabs(D[i]);
max = i;
}
printf("\n\nMax. po modulu otklonenie:\n");
printf("max|g[i]|=%5.4f pri x=x[%d]=%5.4f\n", g, max + 1, X[max]);
}
void metodgaussa(float A[m][m], float B[m], float C[m])
{
int i, k, j;
float sum;
for (i = 0; i<m - 1; i++)
{
for (k = i + 1; k<m; k++)
{
C[i] = A[k][i] / A[i][i];
A[k][i] = 0;
for (j = i + 1; j<m; j++)
A[k][j] = A[k][j] - C[i] * A[i][j];
B[k] = B[k] - C[i] * B[i];
}
}
for (i = m - 1; i >= 0; i--)
{
sum = 0;
for (j = i + 1; j<m; j++)
sum = sum + A[i][j] * C[j];
C[i] = (B[i] - sum) / (A[i][i]);
}
}
Скриншот работы программы:

Заключение
В результате проделанной работы был описан критерий аппроксимации, способ его минимизации, составлена система нормальных уравнений, параметры которой вычислили при помощи метода Гаусса, рассчитаны отклонения аппроксимирующей функции, а также максимальное по модулю отклонение. Расчёты составлены двумя способами:
-подсчитанные вручную
-подсчитанные на ЭВМ, при помощи составленной программы
Date: 2016-05-25; view: 942; Нарушение авторских прав