
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Системы координат, используемые в геодезической астрономии
|
|
1.1.1. Вспомогательная небесная сфера
| s |
| Рис. 1.1. Прямоугольная и полярная системы координат |
| О |
| X |
| Y |
В прямоугольной системе координат положение светила s определяется тремя линейными координатами X, Y, Z. В полярной системе координат положение светила s задается одной линейной координатой, радиус-вектором R = Оs, и двумя угловыми: углом a между осью X и проекцией радиус-вектора на координатную плоскость XOY, и углом b между координатной плоскостью XOY и радиус-вектором R. Связь прямоугольных и полярных координат описывается формулами
X = R cos b cos a;
Y = R cos b sin a;
Z = R sin b,
где R = 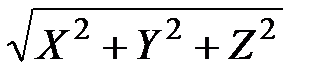 .
.
Эти системы используются в тех случаях, когда линейные расстояния до небесных светил известны (например, для Солнца, Луны, планет, искусственных спутников Земли). Однако для многих светил, наблюдаемых за пределами Солнечной системы, эти расстояния либо чрезвычайно велики по сравнению с радиусом Земли, либо неизвестны. Чтобы упростить решение астрономических задач и обходиться без расстояний до светил, полагают, что все светила находятся на произвольном, но одинаковом расстоянии от наблюдателя. Обычно это расстояние принимают равным единице, вследствие чего положение светил в пространстве может определяться не тремя, а двумя угловыми координатами a и b полярной системы. Известно, что геометрическое место точек, равноудаленных от данной 
| Рис. 1.2. Вспомогательная небесная сфера |
Вспомогательная небесная сфера – воображаемая сфера произвольного или единичного радиуса, на которую проецируются изображения небесных светил (рис. 1.2). Положение любого светила s на небесной сфере определяется при помощи двух сферических координат, a и b:
x = cos b cos a;
y = cos b sin a;
z = sin b.
В зависимости от того, где расположен центр небесной сферы О, различают:
1) топоцентрическую небесную сферу – центр находится на поверхности Земли;
2) геоцентрическую небесную сферу – центр совпадает с центром масс Земли;
3) гелиоцентрическую небесную сферу – центр совмещен с центром Солнца;
4) барицентрическую небесную сферу – центр находится в центре тяжести Солнечной системы.
1.1.2. Основные круги, точки и линии небесной сферы
Основные круги, точки и линии небесной сферы изображены на рис. 1.3.
| Рис. 1.3. Основные круги, точки и линии небесной сферы |
 Одним из основных направлений относительно поверхности Земли является направление отвесной линии, или силы тяжести в точке наблюдения. Это направление пересекает небесную сферу в двух диаметрально противоположных точках – Z и Z'. Точка Z находится над центром и называется зенитом, Z' – под центром и называется надиром.
Одним из основных направлений относительно поверхности Земли является направление отвесной линии, или силы тяжести в точке наблюдения. Это направление пересекает небесную сферу в двух диаметрально противоположных точках – Z и Z'. Точка Z находится над центром и называется зенитом, Z' – под центром и называется надиром.
Проведем через центр плоскость, перпендикулярную отвесной линии ZZ'. Большой круг NESW, образованный этой плоскостью, называется небесным (истинным) или астрономическим горизонтом. Это есть основная плоскость топоцентрической системы координат. На ней имеются четыре точки: S – точка юга, N – точка севера, W – точка запада, E – точка востока. Прямая NS называется полуденной линией.
Прямая PNPS, проведенная через центр небесной сферы параллельно оси вращения Земли, называется осью мира.
Точка PN – северный полюс мира;
PS – южный полюс мира. Вокруг оси мира происходит видимое суточное движение небесной сферы.
Проведем через центр небесной сферы плоскость, перпендикулярную оси мира PNPS. Большой круг QWQ'E, образованный в результате пересечения этой плоскостью небесной сферы, называется небесным (астрономическим) экватором. Здесь Q – верхняя точка экватора (над горизонтом), Q' – нижняя точка экватора (под горизонтом). Небесный экватор и небесный горизонт пересекаются в точках W и E.
Плоскость PNZQSPSZ'Q'N, содержащая в себе отвесную линию и ось мира, называется истинным (небесным) или астрономическим меридианом. Это плоскость параллельна плоскости земного меридиана и перпендикулярна к плоскости горизонта и экватора. Ее называютначальной координатной плоскостью.
Проведем через ZZ' вертикальную плоскость, перпендикулярную небесному меридиану. Полученный круг ZWZ'E называется первым вертикалом.
Большой круг ZsZ', по которому вертикальная плоскость, проходящая через светило s, пересекает небесную сферу, называется вертикалом, или кругом высот светила.
Большой круг PNsPS, проходящий через светило перпендикулярно небесному экватору, называется кругом склонения светила.
| Рис. 1.4. Круги и точки небесной сферы, связанные с видимым годичным движением Солнца |

| ¤ |
Малый круг аsа', проходящий через светило параллельно небесному горизонту, называется кругом равных высот, или альмукантаратом.
В первом приближении орбита Земли может быть принята за плоскую кривую – эллипс, в одном из фокусов которого находится Солнце. Плоскость эллипса, принимаемого за орбиту Земли, называетсяплоскостью эклиптики.
В сферической астрономии принято говорить о видимом годичном движении Солнца (рис. 1.4).Большой круг ЕgЕ'd, по которому происходит видимое движение Солнца в течение года, называется эклиптикой. Плоскость эклиптики наклонена к плоскости небесного экватора на угол e, в настоящее время примерно равный 23.5о. На рис. 1.4 показаны:
g – точка весеннего равноденствия; d – точка осеннего равноденствия; Е – точка летнего солнцестояния; Е' – точка зимнего солнцестояния; RNRS – ось эклиптики; RN – северный полюс эклиптики; RS – южный полюс эклиптики; e – наклон эклиптики к экватору.
1.1.3. Системы сферических координат
Для определения сферической системы координат на сфере выбирают два взаимно перпендикулярных больших круга, один из которых называют основным, а другой – начальным кругомсистемы.
В геодезической астрономии используются следующие системы сферических координат:
1) горизонтальная система координат;
2) первая и вторая экваториальные системы координат.
Название систем обычно соответствует названию больших кругов, принятых за основной. Рассмотрим эти системы координат подробнее.
Горизонтальная система координат
Горизонтальная система координат показана на рис. 1.5.
| Рис. 1.5. Горизонтальная система координат |
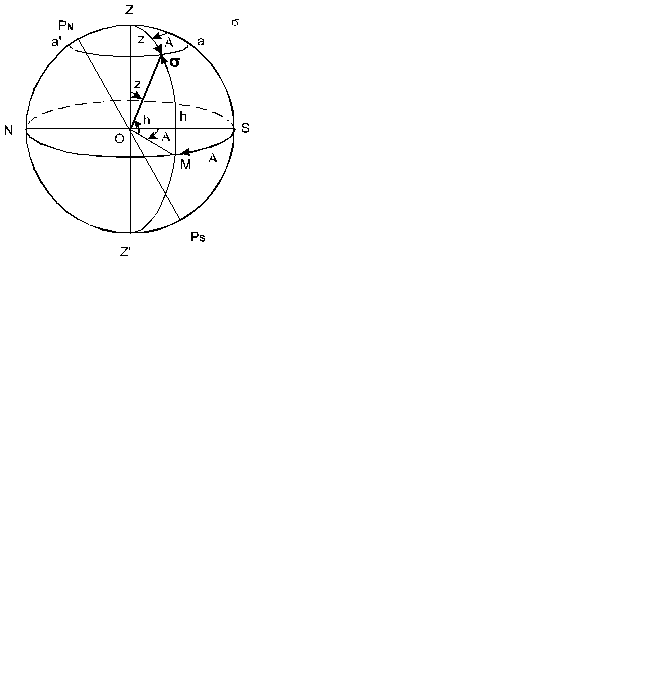 Основной круг в этой системе – астрономический горизонт SMN. Его геометрические полюса – Z (зенит) и Z' (надир).
Основной круг в этой системе – астрономический горизонт SMN. Его геометрические полюса – Z (зенит) и Z' (надир).
Начальный круг системы – небесный меридиан ZSZ'N.
Начальная точка системы – точка
юга S.
Определяющий круг системы – вертикал ZsZ'.
Первая координата горизонтальной системы – высота h, угол между плоскостью горизонта и направлением на светило ÐМОs или дуга вертикала от горизонта до светила ÈMs. Высота отсчитывается от горизонта
и может принимать значения
-90о £ h £ 90о.
Иногда вместо высоты h используется зенитное расстояние – угол между отвесной линией и направлением на светило ÐZОs или дуга вертикала ÈZs. Зенитное расстояние есть дополнение до 90о высоты h:
z = 90о – h.
Date: 2016-05-14; view: 1119; Нарушение авторских прав