
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Коэффициенты ковариации и парной корреляции
|
|
Для количественной оценки тесноты связи используются коэффициент ковариации и линейный коэффициент корреляции, который был впервые введен в начале 90-х годов прошлого столетия английским математиком К. Пирсоном.
Коэффициент ковариации – характеристика тесноты связи показателей 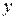 и
и  , и вычисляется по формуле:
, и вычисляется по формуле:
 .
.
Знак ковариации определяется тем, что при прямой связи между  и
и 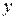 положительные отклонения от
положительные отклонения от  умножаются на положительные отклонения от
умножаются на положительные отклонения от 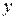 , а отрицательные отклонения на отрицательные.
, а отрицательные отклонения на отрицательные.
При обратной связи наоборот: положительные отклонения от  умножаются на отрицательные отклонения от
умножаются на отрицательные отклонения от 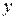 , а отрицательные отклонения от
, а отрицательные отклонения от  на положительные отклонения от
на положительные отклонения от 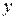 .
.
Поэтому ковариация положительна при прямой связи между  и
и 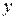 и отрицательна при обратной связи. Если между
и отрицательна при обратной связи. Если между  и
и 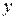 связь отсутствует, то ковариация равна 0.
связь отсутствует, то ковариация равна 0.
Прежде чем вывести формулу коэффициентов корреляции напомним определения дисперсии ( ) и среднего квадратического отклонения (
) и среднего квадратического отклонения ( ).
).
Дисперсия – средний квадрат отклонений индивидуальных значений признака от средней арифметической:
 (1)
(1)
 (2)
(2)
Первая формула применяется для несгруппированных данных, вторая – для сгруппированных данных (вариационного ряда).
Формулу для расчета дисперсии после некоторых преобразований можно привести к следующему виду:
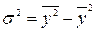
т.е. дисперсия равна разности среднего квадрата значений признака и квадрата среднего значения признака:
где  ;
;  .
.
Или если дисперсия взвешивается:
 ,
, 
Среднее квадратическое отклонение ( ) представляет собой корень квадратный из дисперсии:
) представляет собой корень квадратный из дисперсии: 
Среднее квадратическое отклонение – величина именованная, имеет размерность усредняемого признака.
В теории разработаны и на практике применяются различные модификации формул расчета коэффициента корреляции:

Используя математические свойства средней, получаем следующую формулу для коэффициента парной корреляции – показателя тесноты связи для линейных однофакторных зависимостей:
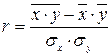
Преобразование данной формулы позволяет получить следующую формулу линейного коэффициента корреляции:
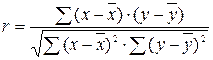
Вычисление коэффициента корреляции по предыдущей формуле является достаточно трудоемкой операцией. Выполнив несложные преобразования, можно получить следующую формулу для расчета линейного коэффициента корреляции:

Линейный коэффициент корреляции изменяется в пределах от –1 до +1; т.е.  . Интерпретацию выходных значений коэффициента корреляции можно представить в табл.1.
. Интерпретацию выходных значений коэффициента корреляции можно представить в табл.1.
Таблица 1. – Оценка линейного коэффициента корреляции
| Значение линейного коэффициента связи | Характер связи | Интерпретация связи |

| Отсутствует | |

| Прямая | С увеличением  увеличивается увеличивается 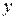
|

| Обратная | С увеличением  уменьшается уменьшается 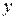 , и наоборот , и наоборот
|

| Функциональная | Каждому значению факторного признака строго соответствует одно значение результативного признака |
До 
| Практически отсутствует | |

| Слабая | |

| Умеренная | |

| Сильная |
3. Оценка существенности линейного коэффициента корреляции
После определения линейного коэффициента корреляции возникает необходимость оценки его существенности, дающая возможность распространить выводы по результатам выборки на генеральную совокупность. В зависимости от объема выборочной совокупности предлагаются различные методы оценки существенности линейного коэффициента корреляции.
Значимость линейного коэффициента корреляции проверяется на основе  -критерия Стьюдента. При этом выдвигается и проверяется гипотеза (
-критерия Стьюдента. При этом выдвигается и проверяется гипотеза (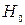 ) о равенстве коэффициента корреляции нулю [
) о равенстве коэффициента корреляции нулю [  ]. При проверке этой гипотезы используется
]. При проверке этой гипотезы используется  -статистика:
-статистика:
 .
.
При выполнении 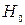 ,
,  -статистика имеет распределение Стьюдента с входными параметрами:
-статистика имеет распределение Стьюдента с входными параметрами:

где  – уровень значимости.
– уровень значимости.
Если расчетное значение  . (табличное), то гипотеза
. (табличное), то гипотеза 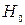 , отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности корреляции
, отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности корреляции  и
и 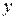 .
.
Данный критерий оценки значимости применяется для совокупности  .
.
При большом числе наблюдений ( ) используется следующая формула
) используется следующая формула  -статистики:
-статистики:

5. Корреляционное отношение
Коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае линейной зависимости между признаками. При наличии же криволинейной зависимости линейный коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен 0, а потому в таких случаях рекомендуется использовать в качестве показателя степени тесноты корреляционное отношение  – характеристику тесноты связи результативного и факторного признаков при их криволинейной зависимости.
– характеристику тесноты связи результативного и факторного признаков при их криволинейной зависимости.
Различают эмпирическое и теоретическое корреляционное отношение. Корреляционное отношение рассчитывают по данным группировки. Расчет корреляционного отношения основан на использовании известной теоремы сложения дисперсий.
Общая дисперсия результативного признака, характеризующая вариацию результативного признака, вызванную всеми действующими на него факторами, определяется:

Она может быть разложена на две составляющие. Первая составляющая – межгрупповая дисперсия, характеризующая ту часть колеблемости результативного признака, которая складывается под влиянием изменения признака-фактора, положенного в основу группировки:

Вторая составляющая – средняя из внутригрупповых дисперсий, оценивающая ту часть вариации результативного признака, которая обусловлена действием других, "случайных" причин.

Разделив межгрупповую дисперсию на общую, получим эмпирический коэффициент детерминации:
 ;
;  .
.
Эмпирический коэффициент детерминации показывает, какая доля вариации результативного признака вызвана признаком, положенным в основание группировки. Чем больше эта доля, тем сильнее влияние факторного признака на результативный.
Извлекая корень из эмпирического коэффициента детерминации, получаем эмпирическое корреляционное отношение:
 или
или  ;
; 
При определении теоретического корреляционного отношения также используются показатели вариации результативного признака. Однако записывают эти показатели несколько иначе, т.к. в их основе лежит знание уравнения регрессии и рассчитанных по нему теоретических значений результативного признака. Показатели вариации, используемые при расчете теоретического корреляционного отношения, выглядят следующим образом:
Общая дисперсия характеризует колеблемость фактических (эмпирических) значений результативного признака 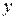 вокруг их средней величины
вокруг их средней величины  , вызванную влиянием на него всех факторов, от которых он зависит:
, вызванную влиянием на него всех факторов, от которых он зависит:
 .
.
Факторная дисперсия характеризует колеблемость теоретических значений признака, рассчитанного по уравнению регрессии  вокруг средней величины
вокруг средней величины  , и объясняет вариацию, вызванную влиянием на результативный признак
, и объясняет вариацию, вызванную влиянием на результативный признак 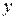 только фактора
только фактора  , входящего в уравнение регрессии:
, входящего в уравнение регрессии:
 .
.
Остаточная дисперсия характеризует колеблемость фактических значений результативного признака 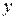 вокруг соответствующих теоретических значений
вокруг соответствующих теоретических значений  , т.е. около линии регрессии. Она вызвана влиянием на результативный признак
, т.е. около линии регрессии. Она вызвана влиянием на результативный признак 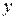 всех прочих факторов, кроме фактора
всех прочих факторов, кроме фактора  , входящего в уравнение регрессии:
, входящего в уравнение регрессии:
 .
.

Разделив факторную дисперсию на общую, получим теоретический коэффициент детерминации который показывает, какая доля общей вариации результативного признака объясняется влиянием фактора  :
:
 ;
; 
Если из этого показателя извлечь квадратный корень, получим теоретическое корреляционное отношение:
 ;
; 
Интерпретация тесноты связи с помощью корреляционного отношения полностью соответствует линейному коэффициенту корреляции.
| <== предыдущая | | | следующая ==> |
| | | Проблемы настоящие: изжога, отрыжка кислым, тупые ноющие боли в подложечной области после еды; наклонность к запорам, похудание, ухудшение аппетита |
Date: 2016-05-25; view: 393; Нарушение авторских прав