Показатели безотказности невосстанавливаемых объектов

К числу широко применяемых количественных характеристик надежности невосстанавливаемых объектов относятся:

— вероятность безотказной работы P (t);

— вероятность отказа Q (t);

— частота отказов a (t);

— интенсивность отказов λ(t);

— средняя наработка до первого отказа Tср.

Вероятность безотказной работы P (t) – это вероятность того, что при определенных условиях эксплуатации в заданном интервале времени не произойдет ни одного отказа.

Вероятность безотказной работы по статистическим данным об отказах оценивается выражением:

, (2.1)

где P*(t) – статистическая оценка вероятности безотказной работы;

N0 – количество изделий в начале испытаний; во время испытаний отказавший объект не восстанавливается и не заменяется исправным;

n (t) – число отказавших объектов за время t.

Пример

На испытания поставлено 1000 образцов однотипных элементов, то есть No = 1000 изоляторов.

При испытании отказавшие элементы не заменялись исправными. За время t отказало 10 изоляторов. Следовательно, P (t) = 0,99 и наша уверенность состоит в том, что любой изолятор из данной выборки не откажет за время t с вероятностью P (t) = 0,99.

Вероятность P (t) – функция убывающая (рисунок 2.1), причем 0≤ P (t)≤1, P (0) = 1, P (∞) = 0. При большом количестве изделий N0статистическая оценка P*(t) практически совпадает с вероятностью P (t).

Рисунок 2.1 – Кривые вероятности безотказной работы P (t) и вероятности отказа Q (t)

Как видно из графика на рисунке 2.1, функция P (t) характеризует изменение надежности во времени и является достаточно наглядной оценкой. Если tр – время безотказной работы, то P (t) = P (tр > t) — вероятность того, что время безотказной работы больше t.

Зависимость P (t) – закон распределения надежности.

Достоинства данного показателя:

— характеризует изменение надёжности во времени;

— даёт возможность наглядно судить о надёжности;

— показатель может быть использован для расчёта надёжности новых систем до их реализации;

— характеризует стоимость изготовления и эксплуатации систем;

— показатель охватывает большинство факторов, влияющих на надёжность.

Недостатки данного показателя:

— показатель характеризует надёжность восстанавливаемых систем до первого отказа и является достаточно полной характеристикой только систем разового пользования;

— показатель не даёт характеристики между временными составляющими цикла эксплуатации;

— эта величина не всегда удобна для оценки надёжности простых элементов при отсутствии старения;

— по этому показателю довольно трудно найти другие показатели надёжности.

На практике более удобна другая характеристика, а именно вероятность отказов (вероятность неисправной работы). Эта характеристика боле удобна, в частности, для сравнения резервированных и нерезервированных ЛЭП и т.п.

Вероятность отказаQ (t) – это вероятность того, что при определенных условиях эксплуатации в заданном интервале времени произойдет хотя бы один отказ.

Вероятность отказа при работе по статистическим данным об отказах оценивается выражением:

. (2.2)

Вероятность отказа Q (t) является возрастающей функцией времени (см. рисунок 2.1). Функция Q (t) характеризует вероятность того, что в заданном интервале времени произойдет хотя бы один отказ: Q (t) = Q (tр < t) — вероятность того, что время безотказной работы меньше t.

Поскольку работоспособность и отказ являются состояниями несовместимыми и противоположными, то их вероятности связаны зависимостью:

P (t) + Q (t) = 1. (2.3)

Частота отказовa (t) — плотность распределения времени безотказной работы или производная от вероятности безотказной работы:

a (t) = q'(t) = — p'(t) (2.4)

Для определения величины a (t) используется следующая статистическая оценка:

, (2.5)

где n (∆t) – количество отказавших изделий в интервале времени ∆t;

N0 – количество изделий в начале испытаний.

Одновременно этот количественный показатель надёжности «а(t)» является дифференциальной функцией распределения вероятностей отказа (плотностью вероятности отказа). Численно равен среднему числу отказов в единицу времени на один объект из начального количества объектов N0 (t=0) или доле начального количества объектов N0 (t=0), отказавших после произвольного, но фиксированного момента времени t, в течение выбранного промежутка времени ∆t:

. (2.6)

Частота отказов «а» или «f» позволяет судить о количестве элементов, выходящих из строя в промежутке времени для невосстанавливаемой системы и довольно просто вычислить количество отказавших систем в интервале ”∆t”,но по её величине нельзя судить о надёжности.

Понятие интенсивность отказов устройства в единицу времени используется как количественная характеристика для математического определения надёжности. Эта величина измеряется в среднем обычно числом отказов за один час. Обратная величина «λ» — наработка до первого отказа в часах — отношение общего времени испытания к общему числу отказов.

Интенсивность отказов λ (t) – это условная плотность распределения времени безотказной работыдля момента времени t при условии, что до этого момент отказа не произошел (интенсивность появления отказов в единицу времени):

, (2.7)

причем P (t) ≤1, то λ (t) ≥а(t).

Для высоконадёжных систем если P (t) = 0.99,то а(t) ≈ λ (t). Ошибка не более 1% и не превышает ошибок статистического определения а(t) и λ (t).

Следует подчёркнуть разницу между величинами а(t) и λ (t). Вероятность а(t) dt характеризует вероятность отказа объекта за интервал времени (t, t+∆t), взятого произвольным образом из группы подобных объектов, причём неизвестно в каком состоянии (работоспособным или неработоспособным) находится объект. Вероятность λ (t) dt характеризует вероятность отказа объекта за интервал (t, t+∆t), взятого из группы подобных объектов, которые остались работоспособными к моменту времени t.

Интегрируя это выражение, получаем выражение, связывающее вероятность безотказной работы и интенсивность отказов:

. (2.8)

Обычно интенсивность отказов изменяется во времени. Лишь в случае экспоненциального закона распределения отказов интенсивность отказов λ (t) = λ = =const.

Со статистической точки зрения интенсивность отказов λ (t) – это отношение количества отказавших изделий в единицу времени к среднему числу изделий, исправно работающих в данный отрезок времени:

, (2.9)

где n (∆t) – количество отказавших изделий в интервале времени ∆t;

– среднее число изделий, исправно работающих в интервале ∆t;

Ni; Ni+1 – соответственно количество изделий, исправно работающих в начале и конце интервала ∆t.

Достоинства данного показателя:

— λ(t) — функция времени и позволяет наглядно установить характерные участки работы системы. Это даёт возможность наметить пути по повышению надёжности;

— по нему довольно просто найти другие характеристики надёжности.

Недостатком является то, что этот показатель используется лишь для невосстанавливаемых объектов.

Как отмечалось выше, показатель Р (или λ) несет наиболее полную информацию о таком свойстве, как безотказность. Однако не всегда в практических условиях таковая имеется. Другой, менее информативной, но простой и наиболее доступной для получения характеристикой является средняя наработка до отказа.

Средней наработкой до отказа Tср -это называется математическое ожидание наработки объекта до первого отказа, которое вычисляется следующим образом:

(2.10)

Таким образом, средняя наработка до отказа графически представляет собой площадь, лежащую под графиком функции P (t).

Статистическая оценка средней наработки до первого отказа при N (t) ≠ 0 может быть получена как:

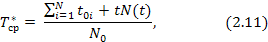
где toi — время до отказа i-го объекта;

t — время наблюдения за N0 объектами;

N — число отказавших объектов за время t.

Этот показатель надёжности является одним из более наглядных количественных характеристик надёжности, но как математическое ожидание не полностью характеризует надёжность восстанавливаемых систем, надо ещё знать дисперсию времени отказов. Величина Тср характеризует работу системы до первого отказа.

Date: 2016-05-25; view: 1067; Нарушение авторских прав