
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Комментарии к задаче
|
|
Четные/нечетные элементы различать по номеру строки или столбца. Ноль рассматривать как “нейтральное” число. Наддиагональное или поддиагональное расположение элемента определять относительно элемента главной диагонали в соответствующей строке или столбце.
Часть 3. МАТРИЧНЫЕ ОПЕРАЦИИ
Постановка задачи:
| “Вычислить Z = <операнд1> <операнд2> <операнд3>” |
где Z – результат операции (матрица, вектор или скалярная величина); операнды 1, 2, 3 представлены в табл. 7.
Правила записи операндов для каждого варианта аналогичны ранее рассмотренным. Например, для 013 варианта задача формулируется следующим образом:
“Вычислить  ” ”
|
Таблица 7
| Цифра варианта | <операнд1> | <операнд2> | <операнд3> |
| (А-Е) | Х | (Х2+1) | |
| (АТ-А)2 | С1И | Sp А | |
| (А+Е)Т | А | С1 | |
| А2 | С2 | С2 | |
| (АТ+А) | АТ | Х | |
| А(АТ+Е) | ХИ | С1·С2 | |
| (А-АТ) | (С1+С2) | С1И | |
| (АТ-Е) | (А-Е)Т | (С2И)2 | |
| (А·АТ) | С2И | (С1-С2) | |
| (АТ)2 | С1 | Х·ХИ |
В таблице использованы следующие обозначения:
 E = (ei,j)n·n - единичная матрица, где ei,j =
E = (ei,j)n·n - единичная матрица, где ei,j = 
C1 - вектор, составленный из элементов главной диагонали матрицы А;
С2 - вектор, составленный из элементов побочной диагонали матрицы А;
SpA-след матрицы А (сумма элементов главной диагонали матрицы А);
т - надстрочный индекс для операции транспонирования матрицы;
и – надстрочный индекс для опрации инвертирования вектора.
Часть 4. УПОРЯДОЧЕНИЕ МАТРИЦЫ
Постановка задачи:
| “Упорядочить <текст1> <текст2> элементы <текст3>” |
Для каждого варианта задача уточняется по табл. 8 по ранее рассмотренному правилу. Задача для 013 варианта:
| “Упорядочить по возрастанию отрицательные элементы столбцов матрицы А”. |
Таблица 8
| Цифра варианта | <текст1> | <текст2> | <текст3> |
| по возрастанию | четные ненулевые | 2-й строки матрицы А | |
| по убыванию абсолютных значений | отрицательные | вектора Х | |
| по возрастанию обратных значений | каждые третьи | побочной диагонали матрицы А | |
| по убыванию модулей обратных значений | нечетные | столбцов матрицы А | |
| по убыванию | ненулевые | первой половины вектора Х | |
| по убыванию обратных значений | не принадлежащие отрезку (-1,0) | строк матрицы Ат | |
| по возрастанию абсолютных значений | каждые вторые | главной диагонали матрицы А | |
| по убыванию | положительные | последней строки матрицы А | |
| по возрастанию абсолютных значений | четные отрицательные | столбцов матрицы Ат | |
| по возрастанию | принадлежащие отрезку [-9,9] | последнего столбца матрицы А |
Часть 5. ВЫЧИСЛЕНИЕ ПАРАМЕТРА МАССИВА
Постановка задачи:
| “Вычислить значение Y = <P1><P2> + <P3>” |
где <P1>, <P2>, <P3> – элементы выражения, представленные в табл. 9. Правила записи выражения аналогичны ранее рассмотренным.
Для 013 варианта постановка задачи имеет вид:
Вычислить значение 
|
Таблица 9
| Цифра варианта | <P1> | <P2> | <P3> |

|   
| 
| |

| 
| 
| |

| 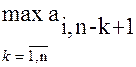
| 
| |

| 
| 
| |

| 
| 
| |
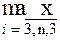
| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
| |

| 
| 
|
СОДЕРЖАНИЕ
Введение 1
Задание 1.
“Обработка одномерных массивов” 2
Задание 2
“Обработка двухмерных массивов” 7
Приложение 12
Date: 2016-05-24; view: 397; Нарушение авторских прав