Ламинарное и турбулентная течение жидкости

Наблюдения показывают, что в природе существует два разных движения жидкости:
1. слоистая упорядоченная течение - ламинарный движение, при котором слои жидкости скользят друг друга, не смешиваясь между собой
2. турбулентная неурегулированная течение, при котором частицы жидкости движутся по сложным траекториям, и при этом происходит перемешивание жидкости.
От чего зависит характер движения жидкости, установил Рейнольдс в 1883 году путем. Эксперименты показали, что переход от ламинарногоруху жидкости к турбулентному движению происходит при определенной скорости (критическая скорость), которая для труб различных диаметров неодинакова: при увеличении диаметра она увеличивается, критическая скорость так же увеличивается при увеличении вязкости жидкости. Рейнольдс вывел общие условия существования ламинарного и турбулентных режимов движения жидкости. По Рейнольдсу режима движения жидкости зависят от безразмерного числа, которое учитывает основные, определяющие это движение: среднюю скорость, диаметр трубы, плотность жидкости и ее абсолютную вязкость. Это число называется числом Рейнольдса:

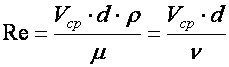(5.16)

Число Рейнольдса, при котором происходит переход от одного режима движения жидкости в другой режим, называется критическим 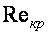. При числе Рейнольдса 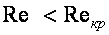наблюдается ламинарный режим движения, при числе Рейнольдса 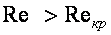- турбулентный режим движения жидкости. Чаще критическое значение числа принимают равным 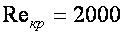, это значение соответствует переходу движения жидкости от турбулентного режима к ламинарного. При переходе от ламинарного режима движения жидкости к турбулентному критическое значение 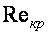имеет большее значение. Критическое значение числа Рейнольдса увеличивается в трубах, сужаются, и уменьшается в тех, что расширяются. Это объясняется тем, что при сужении поперечного сечения скорость движения частиц увеличивается, поэтому тенденция к поперечного перемещения уменьшается.

26)

Турбулентное течение В отличие от ламинарного, в котором близлежащие частицы движутся по практически параллельным траекториям, турбулентное течение жидкости носит неупорядоченный характер. Если использовать подход Лагранжа, то траектории частиц могут произвольно пересекаться и вести себя достаточно непредсказуемо. Движения жидкостей и газов в этих условиях всегда нестационарные, причем параметры этих нестационарностей могут иметь весьма широкий диапазон. Как ламинарный режим течения газа переходит в турбулентный, можно отследить на примере струйки дыма горящей сигареты в неподвижном воздухе. Вначале частицы движутся практически параллельно по неизменяемым во времени траекториям. Дым кажется неподвижным. Потом в каком-то месте вдруг возникают крупные вихри, которые движутся совершенно хаотически. Эти вихри распадаются на более мелкие, те – на еще более мелкие и так далее. В конце концов, дым практически смешивается с окружающим воздухом. Циклы турбулентности Вышеописанный пример является хрестоматийным, и из его наблюдения ученые сделали следующие выводы: Ламинарное и турбулентное течение имеют вероятностный характер: переход от одного режима к другому происходит не в точно заданном месте, а в достаточно произвольном, случайном месте. Сначала возникают крупные вихри, размер которых больше, чем размер струйки дыма. Движение становится нестационарным и сильно анизотропным. Крупные потоки теряют устойчивость и распадаются на все более мелкие. Таким образом, возникает целая иерархия вихрей. Энергия их движения передается от крупных к мелким, и в конце этого процесса исчезает – происходит диссипация энергии при мелких масштабах. Турбулентный режим течения носит случайный характер: тот или иной вихрь может оказаться в совершенно произвольном, непредсказуемом месте. Смешение дыма с окружающим воздухом практически не происходит при ламинарном режиме, а при турбулентном – носит очень интенсивный характер. Несмотря на то, что граничные условия стационарны, сама турбулентность носит ярко выраженный нестационарный характер – все газодинамические параметры меняются во времени. Есть и еще одно важное свойство турбулентности: оно всегда трехмерно. Даже если рассматривать одномерное течение в трубе или двумерный пограничный слой, все равно движение турбулентных вихрей происходит в направлениях всех трех координатных осей. Число Рейнольдса: формула Переход от ламинарности к турбулентности характеризуется так называемым критическим числом Рейнольдса: Recr = (ρuL/µ)cr, где ρ – плотность потока, u – характерная скорость потока; L – характерный размер потока, µ – коэффициент динамической вязкости, cr – течение по трубе с круглым сечением. Например, для течения со скоростью u в трубе в качестве L используется диаметр трубы

27)

РЕЙНОЛЬДСА ЧИСЛО это:

(по имени англ. учёного О. Рейнольдса (О. Reynolds)), один из подобия критериев для течений вязкихжидкостей и газов, характеризующий соотношение между инерц. силами и силами вязкости: Re=rvl/m, где r —плотность, m — коэфф. динамич. вязкости жидкости или газа, v — характерная скорость потока, l —характерный линейный размер. Так, при течении в длинных цилиндрич. трубах обычно l=d, где d — диаметртрубы, a v=vср — средняя по поперечному сечению скорость течения; при обтекании тел l — длина илипоперечный размер тела, а v = v? — скорость невозмущённого потока, набегающего на тело.

28).

Число Рейнольдса определяется следующим соотношением:

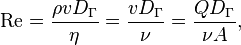
29) где

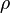· — плотность среды, кг/м³;

· — характерная скорость, м/с;

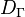· — гидравлический диаметр, м;

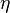· — динамическая вязкость среды, Па·с или кг/(м·с);

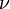· — кинематическая вязкость среды, м²/с ();

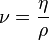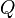· — объёмная скорость потока;

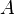· — площадь сечения трубы.

30) Для каждого вида течения существует критическое число Рейнольдса, 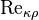, которое, как принято считать, определяет переход от ламинарного течения ктурбулентному. При 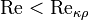течение происходит в ламинарном режиме, при 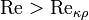возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, такими как изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений и др. Например, для течения (точнее, для стабилизированного изотермического потока) жидкости в прямой круглой^{[ источник не указан 1591 день ]} трубе с очень гладкими стенками 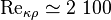. Для движения плёнки жидкости с относительно гладкой поверхностью раздела с газом при двухфазном потоке .

Значения Re выше критического и до определённого предела относятся к переходному (смешанному) режиму течения жидкости, когда турбулентное течение более вероятно, но ламинарное иногда тоже наблюдается — то есть неустойчивая турбулентность. Числу Re_кр 2300 соответствует интервал 2300—10000; для упомянутого примера с тонкими плёнками это 20-120 — 1600.

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение. Напротив, возмущения потока могут значительно снижать величину .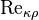

Date: 2016-05-23; view: 966; Нарушение авторских прав