Метод штрафных функций и его применение для оптимизационных задачах

Решение систем линейных уравнений относительно неопределённых множителей не всегда оправданно, так как эти множители не всегда исключаются.

Для исключения этих трудностей используют следующий метод.

Для этого оптимизационное решение может выходить в недопустимую область. Этот выход в область регулируется добавкой к целевой функции и чем больше нарушение ограничений, тем больше добавка именуемая штрафной.

Пусть штрафная функция именуется глобальной штрафной, которая в свою очередь находится в недопустимой области (рисунок 1).

Пусть имеется целевая функция глобального штрафа наибольший экстремум которой находится в недопустимой области. Допустимое решение т. 2 находящаяся на границе.

Рисунок 1

Функция штрафа записывается: .

Данная функция предназначена для уменьшения целевой функции. При нарушении условия дифференцировании функции наиболее благоприятно, когда штрафная функция (Ш) имеет вид квадратичной функции: .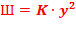

В точке излома дифференциальная функция отсутствует, т.е. сохраняется свойство дифференцируемости функции.

Рост, штрафного элемента приближает т. 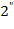к целевой функции экстремума т. 2.

Из-за слишком большой величины функции при переходе , происходит деформирование исходной функции, заменяя задачу её минимизации, задачей минимизирования штрафной функции.

Подбор веса этой функции выявляется в процессе решения задачи.

Пример:

Исходная задача вида:

,

, .

.

где – это функция ограничения.

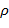– весовой коэффициент задания. Не является предметом оптимизации.

Данная функция ограничения должна образовывать штрафную добавку.

Для сглаживания функции, применяются квадратичные уравнения.

Найти наилучшее распределение мощности между источниками, методом штрафных функций.

Получаем функцию с учётом штрафной добавки :

;

;

;

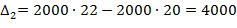
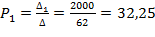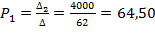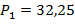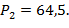
Увеличим влияние штрафной функции

Тогда получим следующую функцию:

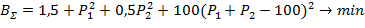
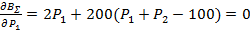
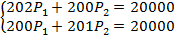
=33,22;

=66,50;

Решение допустимое.

Date: 2016-05-23; view: 383; Нарушение авторских прав