Простая и взвешенная

4. Типичная и нетипичная.

5. Индивидуальная и обобщающая.

82. Что представляет собой формула средней арифметической взвешенной величины?

Варианты ответа:

1. .

2. .

3. .

4. .

5. .

Где х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

f – частота повторения индивидуальных значений признака;

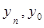‑ последующий и начальный уровень динамического ряда;

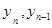‑ последующий и предыдущий уровень динамического ряда.

83. Что представляет собой формула средней арифметической простой величины?

Варианты ответа:

1. .

2. .

3. .

4. .

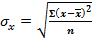5. .

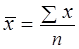Где х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

f – частота повторения индивидуальных значений признака.

84. Средняя хронологическая рассчитывается по формуле:

Варианты ответа:

1. .

2. .

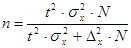3. .

4. .

5. .

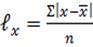Где х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

f – частота повторения индивидуальных значений признака;

t – доверительный коэффициент, зависящий от уровня вероятности Р;

- выборочная дисперсия (дисперсия исследуемого признака в выборочной совокупности);

– предельная ошибка выборки;

N – число единиц в генеральной совокупности;

– среднее значение признака в статистической совокупности;

Где - цена базисного периода;

- количество базисного периода;

- количество отчетного периода.

85. Как рассчитывается средняя квадратическая простая величина?

Варианты ответа:

1. .

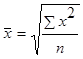2. .

3. .

4. .

5. .

Где х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

f – частота повторения индивидуальных значений признака;

t – доверительный коэффициент, зависящий от уровня вероятности Р;

- выборочная дисперсия (дисперсия исследуемого признака в выборочной совокупности);

– предельная ошибка выборки;

– среднее значение признака в статистической совокупности.

86. Как рассчитывается средняя квадратическая взвешенная величина?

Варианты ответа:

1. .

2. .

3. .

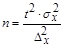4. .

5.

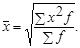
Где х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

f – частота повторения индивидуальных значений признака;

t – доверительный коэффициент, зависящий от уровня вероятности Р;

- выборочная дисперсия (дисперсия исследуемого признака в выборочной совокупности);

– предельная ошибка выборки;

N – число единиц в генеральной совокупности.

87. Как рассчитывается средняя геометрическая взвешенная величина?

Варианты ответа:

1. .

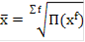2. .

3. .

4. .

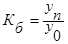5. .

Где

х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

f – частота повторения индивидуальных значений признака;

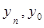‑ последующий и начальный уровень динамического ряда;

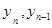‑ последующий и предыдущий уровень динамического ряда;

Где - цена базисного периода;

- количество базисного периода;

- количество отчетного периода.

88. Как рассчитывается средняя геометрическая простая величина?

Варианты ответа:

1. .

2. .

3. .

4. .

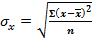5. .

Где

х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

‑ соответственно сумма и число цепных абсолютных приростов;

П – знак произведения признака.

89. Что представляет собой средняя гармоническая взвешенная величина?

Варианты ответа:

1. .

2. .

3. .

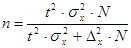4. .

5. .

Где

х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

‑ соответственно сумма и число цепных абсолютных приростов;

t – доверительный коэффициент, зависящий от уровня вероятности Р;

– предельная ошибка выборки;

- выборочная дисперсия;

f – частота повторения индивидуальных значений признака;

N – число единиц в генеральной совокупности;

W – объем совокупности (представляющий собой произведение значения признака на частоту).

90. Что представляет собой средняя гармоническая простая величина?

Варианты ответа:

1. .

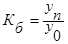2. .

3. .

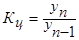4. .

5. .

Где х – индивидуальные значения признака;

n – число статистических единиц в совокупности;

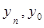‑ последующий и начальный уровень динамического ряда;

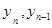‑ последующий и предыдущий уровень динамического ряда;

t – доверительный коэффициент, зависящий от уровня вероятности Р;

– предельная ошибка выборки;

- выборочная дисперсия.

91. Что такое мода?

Варианты ответа:

Варианта, наиболее часто встречающаяся в совокупности.

2. Варианта, находящаяся в середине вариационного ряда.

3. Варианта, с максимальной величиной признака.

4. Варианта, с минимальной величиной признака.

5. Варианта, с максимальной суммой накопленных частот.

92. Что такое статистическая медиана?

Варианты ответа:

1. Варианта с наибольшей локальной частотой.

2. Варианта, находящаяся в конце вариационного ряда.

Варианта, находящаяся в середине вариационного ряда.

4. Варианта с наименьшей локальной частотой.

5. Варианта, с максимальной суммой накопленных частот.

93. Укажите, как изменится средняя величина, если все веса в 2 раза увеличить?

Варианты ответа:

Не изменится.

2. Уменьшится в два раза.

3. Возрастет в четыре раза.

4. Возрастет в квадрате.

5. Изменение средней предсказать нельзя.

94. Укажите основное назначение средней геометрической величины?

Варианты ответа:

1. Для расчета среднего значения признака в интервальном ряду с равными интервалами.

2. Для расчета среднего значения признака в ранжированном ряду.

Date: 2016-05-18; view: 751; Нарушение авторских прав