Условия на границе раздела двух магнетиков

Установим связь для векторов и на границе раздела двух однородных магнетиков с магнитной проницаемостью и при отсутствии на границе тока проводимости.

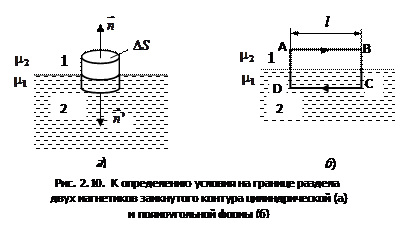Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом магнетике, другое – во втором (рис. 2.10, а).

Основания 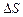настолько малы, что в пределах каждого из них вектор одинаков. Согласно теореме Гаусса

,

поскольку нормал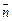и и к основаниям цилиндра направлены противоположно: .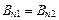

С учетом соотношения (2.6) нормальные составляющие

.

Вблизи границы раздела двух магнетиков 1 и 2 построим небольшой замкнутый прямоугольный контур АВСDA длиной (рис. 2.10, б). Согласно теореме о циркуляции вектора

,

поскольку токов проводимости на границе раздела нет. Отсюда

.

Знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам BC и DA ничтожно малы.

Поэтому .

С учетом соотношения (2.6) получим:

.

Таким образом, при переходе через границу раздела двух магнетиков нормальная составляющая вектора и тангенциальная составляющая вектора изменяются непрерывно, а тангенциальная составляющая вектора 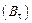и нормальная составляющая вектора претерпевают скачок.

Date: 2016-05-18; view: 565; Нарушение авторских прав