Тема «Многоугольники

Вписанные и описанные многоугольники»

81. Гипотенуза прямоугольного треугольника равна 15 см. Найдите радиус окружности, описанной около треугольника.

82. Острый угол прямоугольного треугольника равен 37°. Найдите углы, под которыми видны катеты из центра описанной около него окружности.

83. Найдите радиус окружности, описанной около равнобедренного треугольника, боковая сторона которого равна 10 см, а один из углов равен 140°.

84. Постройте треугольник АВС по стороне АС = b, углу А и радиусу R описанной окружности.

85. Постройте равнобедренный треугольник по боковой стороне а и радиусу описанной окружности R.

86. Можно ли описать окружность около четырехугольника, углы которого, взятые последовательно, относятся как 2:3:4:11?

87. Найдите углы вписанного в окружность четырехугольника, если противоположные углы относятся как 2:3 и 4:5.

88. Постройте четырехугольник, который можно вписать в окружность, по трем его сторонам и одной диагонали.

89. В прямоугольный треугольник с острым углом 40° вписана окружность. Найдите углы, под которыми видны стороны данного треугольника из центра вписанной в него окружности.

90. Углы треугольника относятся как 2:3:4. Под какими углами видны стороны треугольника из центра вписанной окружности.

91. Найдите радиус окружности, вписанной в ромб, большая диагональ которого равна 18 см, тупой угол равен 120°.

92. Найдите длину окружности, описанной около прямоугольного треугольника с катетом b и прилежащим к нему острым углом a.

93. Найдите радиус окружности, описанной около трапеции, стороны которой равны 2 см, 1 см, 1см, 1 см.

94. Три последовательные стороны описанной около круга трапеции равны 13 см, 8 см и 13 см. Найдите радиус круга.

95. В равнобедренную трапецию с основаниями 18 см и 6 см вписан круг. Найдите его радиус и углы трапеции.

96. Докажите, что во вписанном в окружность четырехугольнике внешний угол равен противолежащему внутреннему углу.

97. Через точку А дуги ВС проведены две хорды АD и АЕ, пересекающие хорду ВС в точках F и G соответственно. Докажите, что четырехугольник DFGЕ можно вписать в окружность.

98. Докажите, что во вписанном в окружность четырехугольнике биссектриса внутреннего угла пересекается с биссектрисой противолежащего внешнего угла на окружности.

99. В треугольнике АВС биссектриса угла С пересекает в точке D перпендикуляр, проведенный из середины стороны АВ. Докажите, что около четырехугольника АDВС можно описать окружность.

100. Две окружности пересекаются в точках А и В; САD – секущая (точки С и D принадлежат окружностям). Через точки D и С проведены касательные до пересечения в точке Е. Докажите, что около четырехугольника ВСЕD можно описать окружность.

Тема «Площади плоских фигур»

121. Площадь прямоугольника равна 520 м², а отношение его сторон равно 2:5. Найдите периметр данного прямоугольника.

122. Стороны параллелограмма равны 5 см и 11 см. Найдите его площадь, если один из углов равен 30°.

123. Найдите площадь ромба со стороной 24 см и углом 120°.

124. Найдите площадь параллелограмма, периметр которого равен 42 см, а высоты равны 8 см и 6 см.

125. Найдите периметр ромба, площадь которого равна 48 см², а острый угол равен 30°.

126. Найдите площадь равнобедренной трапеции, у которой основания равны 8 см и 18 см, а боковая сторона равна средней линии.

127. В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.

128. Стороны треугольника относятся как 3:25:26. Его площадь равна 144 см². Найдите периметр данного треугольника.

129. Основание равнобедренного треугольника равно 5 см. Медианы боковых сторон перпендикулярны. Найдите площадь данного треугольника.

130. В прямоугольном треугольнике сумма катетов равна m, а гипотенуза равна с. Найдите площадь треугольника, не вычисляя его катетов.

131. В четырехугольнике АВСD диагонали перпендикулярны и равны 4 см и 11 см. Найдите его площадь.

132. Точка касания круга, вписанного в прямоугольный треугольник, делит гипотенузу на части, равные 4 см и 6 см. Найдите площадь этого круга.

133. Докажите, что медианы треугольника разбивают его на шесть равновеликих треугольников.

134. Найдите отношение площадей треугольника и четырехугольника, на которые рассекается данный треугольник своей средней линией.

Тема «Координаты и векторы»

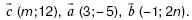141. Даны векторы. Найдите числа m и n.

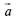
142. Дан вектор. Найдите координаты вектора такого что сонаправлен с и его длина в два раза больше, чем у вектора.

143. Найдите координаты точки А (х; у), если она симметрична точке

В (–20; 11) относительно точки М (0; –5).

144. Найдите координаты точки С (х; у), если она принадлежит оси абсцисс и одинаково удалена от точек А (–14; 5) и В (3; 8).

145. Даны точки М (–2; 6), К (1; 2) и L (4; –2). Определите, принадлежат ли данные точки одной прямой.

146. Определите, будет ли треугольник ОРQ равносторонним, если О – начало координат и Р (5; 6), Q (–6; 5).

147. Найдите сумму векторов:

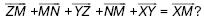148. Верно ли равенство:

149. В окружности с центром в точке О проведены диаметр АВ и радиус ОС.

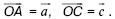Пусть Необходимо выразить векторы через векторы и доказать, что угол АСВ прямой.

150. Точка М делит отрезок КL в отношении 2:3. Найдите координаты вектора

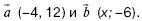151. Даны векторы Найдите значение х, при котором данные векторы будут перпендикулярны.

152. Дан треугольник ABС и точка G – точка пересечения его медиан. Докажите, что

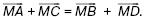153. Дан параллелограмм АВСD. Докажите, что для любой точки М

154. На сторонах угла О отложены отрезки ОА = ОВ. Докажите, что вектор лежит на биссектрисе угла О.

155. В треугольнике АВС точка М – середина стороны ВС. Точка D симметрична точке А относительно точки М.

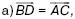Докажите, что:

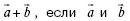156. Найдите модуль вектора единичные векторы, и угол между ними равен 60°.

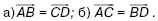157. Две равные окружности пересекаются в точках М и N. Через них проведены две параллельные секущие. Первая пересекает окружности в точках А и В, вторая – в точках С и D. Докажите, что:

158. Запишите условие того, что четырехугольник АВСD является: а) параллелограммом; б) трапецией.

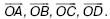159. Даны четыре вектора. Запишите условие того, что точка О является точкой пересечения диагоналей АС и ВD выпуклого четырехугольника АВСD.

160. В окружность с центром О вписан правильный пятиугольник АВСDЕ. Докажите, что

Date: 2016-05-18; view: 440; Нарушение авторских прав