Теория двойственности

Понятие двойственности рассмотрим на примере задачи оптимального использования сырья. Пусть на предприятии решили рационально использовать отходы основного производства. В плановом периоде появились отходы сырья m видов в объемах единиц . Из этих отходов, учитывая специализацию предприятия, можно наладить выпуск n видов неосновной продукции. Обозначим через норму расхода сырья i-го вида на единицу j-й продукции, 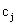- цена реализации единицы j-й продукции (реализация обеспечена). Неизвестные величины задачи: 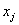— объемы выпуска j -й продукции, обеспечивающие предприятию максимум выручки.
Математическая модель задачи:
(2.23)
(2.24)
(2.25)
Предположим далее, что с самого начала при изучении вопроса об использовании отходов основного производства на предприятии появилась возможность реализации их некоторой организации. Необходимо установить прикидочные оценки (цены) на эти отходы. Обозначим их .
Оценки должны быть установлены исходя из следующих требований, отражающих несовпадающие интересы предприятия и организации:
1) общую стоимость отходов сырья покупающая организация стремится минимизировать;
2) предприятие согласно уступить отходы только по таким ценам, при которых оно получит за них выручку, не меньшую той, что могло бы получить, организовав собственное производство.
Эти требования формализуются в виде следующей ЗЛП.
Требование 1 покупающей организации – минимизация покупки:
(2.26)
Требование 2 предприятия, реализующего отходы сырья, можно сформулировать в виде системы ограничений. Предприятие откажется от выпуска каждой единицы продукции первого вида, если , где левая часть означает выручку за сырьё идущее на единицу продукции первого вида; правая – её цену.
Аналогичные рассуждения логично провести в отношении выпуска продукции каждого вида. Поэтому требование предприятия, реализующего отходы сырья, можно формализовать в виде сл. системы ограничений:
(2.27)
По смыслу задачи оценки не должны быть отрицательными:
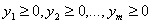. (2.28)
Переменные 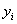называют двойственными оценками или объективно обусловленными оценками.
Задачи (2.23) - (2.25) и (2.26) - (2.28) называют парой взаимно двойственных ЗЛП.
Между прямой и двойственной задачами можно установить следующую взаимосвязь:
1. Если прямая задача на максимум, то двойственная к ней — на минимум, и наоборот.
2. Коэффициенты целевой функции прямой задачи являются свободными членами ограничений двойственной задачи.
3. Свободные члены ограничений прямой задачи являются коэффициентами целевой функции двойственной.
4. Матрицы ограничений прямой и двойственной задач являются транспонированными друг к другу.
5. Если прямая задача на максимум, то ее система ограничений представляется в виде неравенств типа . Двойственная задача решается на минимум, и ее система ограничений имеет вид неравенств типа .
6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной — числу переменных прямой.
7. Все переменные в обеих задачах неотрицательны.

Основные теоремы двойственности и их экономическое содержание

Теорема. Для любых допустимых планов и 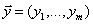прямой и двойственной ЗЛП справедливо неравенство , т.е.
(2.29)
– основное неравенство теории двойственности.
Теорема (критерий оптимальности Канторовича).
Если для некоторых допустимых планов и пары двойственных задач выполняется неравенство , то и являются оптимальными планами соответствующих задач.
Теорема (малая теорема двойственности).
Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
Теорема. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.
Теорема (о дополняющей нежесткости)
Для того, чтобы планы и пары двойственных задач были оптимальны, необходимо и достаточно выполнение условий:
(2.30)
(2.31)
Условия (2.30), (2.31) называются условиями дополняющей нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.
Экономически это означает, что если по некоторому оптимальному плану производства расход i -го ресурса строго меньше его запаса , то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i -я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.
Теорема (об оценках). Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи математического программирования, точнее
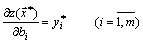(2.32)