Оптимальное управление полётом по маршруту

Цель работы

1. Изучение способов управления движением летательного аппарата (ЛА) по линии заданно-го пути (ЛЗП): а) курсового; б) путевого; в) маршрутного.

2. Изучение критерия оптимального полёта по маршруту–функционала обобщённой работы.

3. Изучение законов управления боковым отклонением и отклонением высоты.

4. Изучение алгоритма траекторного управления.

5. Изучение численного решения задачи оптимизации маршрутного управления.

6. Определение оптимальных коэффициентов по отклонению и по скорости (k_Z и k_Ż) методом чисел Фибоначчи.

2. Способы управления движением летательного аппарата по линии заданного пути [2, 3]

Управление движением ЛА по заданной траектории осуществляется путём последова-тельного его вывода в поворотные пункты маршрута (ППМ). При путевом способе управле-ние движением в боковом направлении осуществляется с помощью путевого пеленга ППМ Y_W (рис.1, а). Для полёта по ЛЗП и последующего вывода ЛА в ППМ вектор путевой скорос-ти W должен быть направлен в заданную точку. Для этого угол путевого пеленга Y_W необхо-димо выдерживать равным нулю:

Y_W= ЗПУ – ФПУ = ЗПУ –(ИК +a)=0, (1)

где ЗПУ –заданный путевой угол, ФПУ –фактический путевой угол, ИК –истинный курс, a–угол сноса. Это условие обеспечит полёт к заданной точке по кратчайшему расстоянию по ортодромии, проходящей через данную точку и ППМ. Это достоинство путевого способа. Однако при отклонении ЛА от ЛЗП способ не обеспечивает выхода на неё, что является его недостатком. Если параметры ветра неизвестны, то экипаж считает угол сноса равным нулю, и путевой способ превращается в курсовой.

В курсовом способе управление движением в боковом направлении осуществляется с помощью курсового пеленга Y_V (рис.1, б), который выдерживается равным нулю. При отсут-ствии ветра ЛА будет подходить к ППМ по кратчайшему расстоянию, а в условиях ветра – по сложной траектории, не совпадающей с ЛЗП. В ряде случаев возможны значительные от-клонения линии фактического пути (ЛФП) от ЛЗП и значительные отклонения ФПУ от ЗПУ.

Маршрутный способ полёта по ЛЗП и вывода ЛА в ППМ реализуется, когда обеспечи-вается непрерывное определение и индикация координат Z и S. Задача решается в системе зе-мных координат, одной из осей которой служит ЛЗП, а второй – перпендикулярное к ней на-правление (рис.1, в). Управляющий параметр в маршрутном способе – линейное боковое ук-лонение от ЛЗП Z. При Z =0 ЛА следует по ЛЗП и обеспечивается его выход в ППМ. При уп-равлении маршрутным способом форма ЛФП определяется формой ЛЗП. Если точки излома маршрута соединяются отрезками ортодромии, то маршрутный способ обеспечивает движе-ние по ортодромии. При отклонении от заданного маршрута ЛА выводится на ЛЗП и в этом преимущество маршрутного метода.

				в)

Рис.1. Способы управлением полёта по ЛЗП.

Оптимальное управление полётом по маршруту

Задача оптимизации траекторного управления при маршрутном методе навигации обы-чно решается на основе методов аналитического конструирования регуляторов. Наиболее строгое решение задачи получается при использовании полных нелинейных уравнений прос-транственного уравнения ЛА и системы управления. Однако при таком подходе трудно учесть иерархию управления, в частности, наличие навигационного и пилотажного комплек-сов, каждый из которых имеет свой контур управления, причём навигационный комплекс яв-ляется старшим уровнем по отношению к пилотажному комплексу, выполняющему функции исполнения. Навигационный комплекс в своей управляющей части должен формировать за-дающее воздействие для пилотажного комплекса в виде заданного угла крена, заданного уг-ла тангажа, заданной скорости, заданной перегрузки и т.д.

Именно эти задающие воздействия целесообразно рассматривать как управления при решении задачи оптимизации траекторного управления.

С учётом иерархического принципа управления модель траекторного движения ЛА сос-тавляется в отклонениях от заданной траектории. Затем задаётся критерий оптимизации, ко-торый может быть терминальным или нетерминальным. Терминальные задачи оптимизации характерны для таких этапов полёта, как посадка, приземление, самонаведение, стыковка и т.п. Оптимизация по терминальным критериям приводит к нестационарным управлениям, за-висящим от относительного времени и конечного момента времени.

Для стационарных режимов характерны стационарные и нетерминальные оптимальные управления. Для маршрутного полёта, а также многих видов маневрирования, допустима не-терминальная оптимизация. В интересах простоты задачи оптимизации целесообразным яв-ляется применение критерия оптимизации в виде функционала обобщённой работы (ФОР), предложенного для процессов, описываемых уравнениями [5]:

(2)

Оптимальными в смысле минимума функционала

(3)

являются уравнения

(4)

где – решение уравнения Ляпунова

(5)

при граничном условии

В уравнениях (2)–(5) х (t)=(х ₁, х ₂, …, х_n)^T – вектор состояния; u =(u ₁, u ₂, …, u_m)^T – вектор управления; f_i, φ _{i j} , Q _З, V _З – заданные непрерывные функции времени; > 0 – заданные ко-эффициенты.

Левый член ФОР в (3) (терминальный член) ”отвечает” за вывод управляемого объекта в момент времени t _кон= t ₂ в окрестность желаемой ”цели”. Средний член ”отвечает” за качес-тво переходных процессов и соблюдение ограничений. Правый член ФОР может выражать энергетические и информационные затраты, или и то и другое вместе. В целом правый член допускает следующую интерпретацию. При решении задач синтеза системы управления он влияет прежде всего на структуру и параметры синтезируемого интерфейса, связывающего систему управления с объектом управления (цифроаналоговые преобразователи, экстраполя-торы, исполнительные устройства). При оптимальном управлении правый член всегда равен нулю [5].

Главным достоинством оптимизации на основе минимизации ФОР является алгоритми-ческая и вычислительная простота, поскольку решение уравнения Ляпунова не представляет трудностей. Минимизация ФОР вместо традиционных методов (например, минимизации ме-тодом динамического программирования) для сложных многоразмерных нелинейных задач оптимизации позволяет на два-три и более порядков сократить вычислительные затраты на стадии проектирования и требуемую вычислительную производительность в режиме реаль-ного времени.

Поставим задачу нахождения g_З= k_Z Z + k_Ż Ż с помощью критерия оптимального полё-та по маршруту в виде частного случая ФОР [7]:

Т

I = ∫ Z ² (t, k) dt, (6)

где Т – время переходного процесса, k – оптимизируемый коэффициент (k_Z или k_Ż). Левый член ФОР (3) можно положить равным нулю. Правый член ФОР равен нулю, т. к. система управления спроектирована оптимальной с точки зрения отработки управляющих сигналов. Функционал (6) имеет чёткий физический смысл. Он учитывает площадь подынтегральной кривой Z (t), что обеспечивает минимум отклонений от ЛЗП.

Таким образом задача оптимизации управления по маршруту сводится к тому, чтобы найти такую зависимость угла крена от переменных состояния g_З= k_Z Z + k_Ż Ż под действием которой система из состояния Z (0), Ż (0) переходила бы в состояние Z (t _кон)=0, Ż (t _кон)=0 и при этом функционал I принимал наименьшее значение.

Рассмотрим законы управления по каналам элеронов и руля высоты [1]. При стабили-зации ЛА на траектории обычно сигнал датчика Z вводят только в канал элеронов, а сигнал датчика Δ H = H – H _З (где H _З – заданная высота полёта), как правило, вводят только в канал ру-ля высоты. В результате для режима стабилизации ЛА на траектории законы управления по каналам элеронов, руля направления и руля высоты в общем виде могут быть представлены как [1]

(7)

где γ – угол крена; υ – угол тангажа; ω _x, ω _y, ω _z – проекции вектора угловой скорости разворо-та самолёта ω на оси связанной системы координат.

Число слагаемых в правых частях системы (7) соответствует числу действительно при-меняемых в реальных системах датчиков. Особенности конкретных сервоприводов рулей учитываются передаточными функциями при входных параметрах.

Часто законы управления по каналам элеронов и руля высоты представляются в виде

(8)

где (9)

Величины g_З и u_З при этом представляют «заданные» значения углов g и u, функциона-льно связанные с Z иΔ H. Запись (8) законов управления намечает путь к упрощению систем уравнений, описывающих процессы стабилизации ЛА на траектории. Действительно, если предположить, что система управления мгновенно отрабатывает заданные значения углов крена и тангажа, так что g≡g_З, u≡u_З, то отпадает необходимость в рассмотрении уравнений (8), и законы управления боковым отклонением и отклонением высоты принимают вид

(10)

выражающий связь уже не между входными и выходными параметрами каналов элеронов и руля высоты, а между управляющими (g, u) и траекторными (Z, Δ H) параметрами системы управления [1].

Траекторные параметры, характеризующие движение центра масс ЛА изменяются во времени сравнительно медленно. Параметры, характеризующие движение вокруг центра масс, изменяются во времени сравнительно быстро. С помощью этих параметров можно эф-фективно воздействовать на движение центра масс. В связи с этим в качестве управляющих удобно использовать параметры, характеризующие движение самолёта вокруг центра масс, т.е. угловые параметры, что и отражено уравнениями (10). Практически запись (10) законов управления означает пренебрежение переходными процессами движения самолёта вокруг центра масс ввиду их малой длительности по сравнению с длительностью переходных про-цессов движения центра масс.

4. Алгоритм траекторного управления [6]

Оптимальное управление полётом ЛА по маршруту осуществляется с помощью алгори-тма траекторного управления (АТУ), который представлен на рис.2. АТУ реализуется в БЦВМ.

Входными параметрами АТУ являются траекторные параметры ЛА относительно теку-щей ЛЗП и следующей ЛЗП: S, Z – ортодромические координаты ЛА; Z _max– максимальное допустимое боковое уклонение для использования в законе управления g_З= k_Z Z + k_Ż Ż; ФПУ – фактический путевой угол; V – скорость ЛА; H – высота полёта; H _З – заданная высота полё-та; ЗПУ_i – заданный путевой угол i -й ЛЗП; ЗПУ_i+1 – заданный путевой угол (i +1)-й ЛЗП.

Выходными функциями АТУ являются: закон управления углом крена g_З= k_Z Z + k_Ż Ż и за-кон управления углом тангажа u_З.

Рис.2. Блок-схема алгоритма траекторного управления.

Сигналы V и H позволяют рассчитать линейное упреждение разворота S _у (блок 1). При S > S _у АТУ обеспечивает режим стабилизации по боковому отклонению Z от ЛЗП, причём, при больших отклонениях, когда | Z | > Z _max(блок 3), обеспечивается перевод ЛА на траекто-рию сближения с ЛЗП. Расчёт g_З при этом осуществляется с учётом параметров ФПУ, ЗПУ_i и Z, поскольку отпадает необходимость в сигнале Ż для демпфирования боковых колебаний из-за необходимости скорейшего сближения с ЛЗП (блок 4). При | Z | ≤ Z _maxАТУ обеспечивает управление ЛА по закону g_З= k_Z Z + k_Ż Ż, при этом устойчивость траекторного управления обес-печивается тем, что кроме отклонения Z используется производная по времени Ż, которая обеспечивает демпфирование боковых колебаний (блок 5).

При S ≤ S _у обеспечивается расчёт g_З в зависимости от разности заданных путевых углов i -й и (i +1)-й ЛЗП, а также в зависимости от скорости и высоты полёта V и H (блоки 6 и 7).

Управление в продольной плоскости обеспечивается путём стабилизации высоты отно-сительно H _З. Вычисление u_З осуществляется в зависимости от отклонений высоты полёта от заданной с помощью трёх различных соотношений (блоки 11, 12, 13). При больших отклоне-ниях высоты Δ H от заданной (блоки 9, 10) в закон управления по тангажу входят только по-зиционные параметры (блоки 11, 12), а при малых отклонениях – также и производные от Δ H, что обеспечивает устойчивость процесса стабилизации высоты (блок 13).

5. Математическое моделирование полёта по маршруту [7]

В программе OTU моделирование полёта ЛА по маршруту производится численным интегрированием системы дифференциальных уравнений, которая состоит из уравнений по-лёта в боковой плоскости и уравнений навигации в ортодромической системе координат.

Уравнения динамики полёта ЛА в боковой плоскости вместе с уравнением системы ав-томатического управления (САУ) имеют вид:

(11)

(12)

(13)

(14)

где ω _х, ω _у – проекции вектора угловой скорости на оси связанной системы координат (ССК); – переменная составляющая проекции угловой скорости на ось Y ССК; V – воздушная скорость ЛА; g – угол крена; g_З – заданный угол крена; β – угол скольжения; Y – курсовой угол ЛА (угол между вектором V и ЛЗП); g (Н) – ускорение свободного падения на высоте Н; , , , , – приведённые аэродинамические коэффициенты; ξ _х , ξ _у – коэф-фициенты демпфирования собственных колебаний системы ЛА–САУ относительно осей Х и Y ССК; Ω _х , Ω _у – угловые частоты собственных колебаний системы ЛА–САУ относительно осей Х и Y ССК; Т – постоянная времени интегро-дифференцирующего звена в канале курса САУ.

Коэффициенты дифференциальных уравнений (11)–(14) определяются с помощью вы-ражений = а ₃ q; = а ₄ q; = а ₆ q; = а ₅ q; = а ₂ q ₁, где q = ; q ₁= .

Коэффициенты, входящие в вышеприведённые выражения, являются константами и оп-ределяются через аэродинамические, геометрические и инерционные характеристики ЛА и характеристики САУ:

где 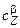, , , , – аэродинамические коэффициенты ЛА; S – площадь крыла; l – – характеристический размер ЛА; m – масса ЛА; I _x, I _y – моменты инерции ЛА относительно осей симметрии ЛА.

Коэффициенты демпфирования собственных колебаний системы ЛА–САУ

Угловые частоты собственных колебаний системы ЛА–САУ

где i _γ, i _β, χ _x, χ _y – коэффициенты законов управления САУ; , – аэродинамические коэффициенты ЛА.

В программе OTU угловые частоты собственных колебаний представлены аппроксима-ционными выражениями

Ω _х = Ω _{х 0} + (μ _х + η _х H)(q –1000); Ω _у = Ω _{у 0} + (μ _у + η _у H)(q –1000),

где Ω _{х 0} , Ω _{у 0}, μ _х , μ _у , η _х , η _у – константы.

Счисление пути ЛА в ортодромической системе координат производится с помощью уравнений навигации

= V cos(ЗПУ –Ψ–β); Ż = V sin(ЗПУ –Ψ–β). (15)

В программе OTU решение системы дифференциальных уравнений движения и навига-ции (11)–(15) производится методом Эйлера с шагом интегрирования h = 0,1 с.

Date: 2016-05-17; view: 1225; Нарушение авторских прав