Часть III. Газовая динамика

Г а з о в а я д и н а м и к а – раздел гидрогазодинамики, изучающий закономерности движения газа с учетом его сжимаемости.

Адиабатное течение

Течение, в котором отсутствует теплообмен между частицами газа, а также между газом и окружающими его поверхностями.

Изоэнтропное течение

Течение газа с постоянной энтропией на всем его протяжении.

Местные параметры

Местными параметрами называют параметры газового потока (абсолютное давление p, температура Т, плотность , удельная энтальпия i, скорость потока ) в том или ином его сечении, а в более общем случае – в той или иной его точке.

Скорость звука

Скорость распространения в среде упругих волн слабой интенсивности именуют скоростью звука.

Обозначают скорость звука а, выражают в м/с.

Дозвуковая скорость

Скорость газа, которая по величине меньше местной скорости звука, называется дозвуковой, .

Сверхзвуковая скорость

Скорость газа, превышающая местную скорость звука, называется сверхзвуковой,

Число Маха

Отношение местной скорости движения газа к скорости звука в том же сечении (в точке) потока называют числом Маха.

Обозначается через М. Из определения: М = .

Уравнение расхода для сжимаемого газа

Уравнение расхода для сжимаемого газа записывается в виде:

,

где – массовый расход газа через канал;

F – площадь сечения канала;

– плотность газа;

– средняя скорость в сечении канала.

Данное уравнение выражает закон сохранения массы вещества для ус-

тановившегося одномерного течения сжимаемого газа в канале с непроницаемыми стенками.

Уравнение обращения воздействия

Уравнение обращения воздействия на газовый поток (уравнение А.Вулиса) записывается в виде:

В правой части этого уравнения каждое слагаемое выражает конкрет-

ное воздействие на скорость движения газа в канале: – геометрическое;

– массовое; dq – тепловое; 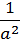dl_тех – механическое воздействие.

Характер каждого воздействия на скорость потока при дозвуковом движении газа один, а при сверхзвуковом – противоположен.

Сопла и диффузоры

Каналы, в которых газовый поток увеличивает свою скорость, называются соплами. Каналы, в которых скорость газового потока уменьшается, именуют диффузорами.

Критическое сечение канала

Сечение канала, в котором скорость газового потока равна местной скорости звука называют критическим сечением.

Критические параметры потока газа

Параметры газа в критическом сечении именуют критическими и обозначают подстрочным индексом «кр», например, р_кр, Т_кр , _кр , i_кр .

Параметры торможения

Параметрами торможения называются такие параметры газового потока, которые имел бы газ при его адиабатном торможении от заданной скорости до нуля.

Обозначается параметры торможения подстрочным индексом «0», то есть .

Расход газа через критическое сечение

Секундный массовый расход газа через критическое сечение канала расчитываеся по формуле

Скорость газа в канале

Скорость движения газа в i-том сечении канала при известном давлении р_i в нем вычисляется по формуле

Максимальная скорость

Скорость газового потока, соответствующая полному преобразованию энтальпии в кинетическую энергию.

Максимальную скорость определяют, используя формулу:

Коэффициент скорости

Отношение скорости газа к критической скорости звука.

Коэффициент скорости обозначается 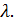Согласно определению

.

Уравнение Бернулли для сжимаемого газа

Уравнение Бернулли для сжимаемого газа, выражающее закон сохранения энергии для одномерного установившегося энергоизолированного потока, записывается в виде:

– скорость;

кинетическая энергия единицы массы газа;

u – внутренняя энергия единицы массы газа;

p – абсолютное давление;

– плотность газа;

– потенциальная энергия давления единицы массы газа.

Библиографический список

1. Алексеев Г.Н. Общая теплотехника. Г. Н. Алексеев. – М.: Высш. шк., 1980. – 552 с.: ил.

2. ГОСТ 30813 – 2002 («Вода и водоподготовка. Термины и определения»).

3. Кудинов В.А., Карташов Э.М. Гидравлика. – М.: Высшая школа, 2008. –199с.

4. Лойцянский Л.Г. Механика жидкости и газа. – М.: Дрофа, 2003. – 803 с.

5. Сайт: WWW.rostplo.ru/sprav/953/.

6. Справочник (Теплоэнергетика и теплотехника; Кн. 4) Под общей ред. Клименко А.В. и Зорина В.М. М.: Издательство МЭИ, 2004– 564 с.

7. Стоцкий Л.Р. Физические величины и их единицы. Справочник.

Л.Р. Стоцкий. – М.: «Просвещение»,1984 – 240 с.

9. Термодинамика. Сборник определений. /Под ред. И.И Новикова. – М.: «Наука», 1984. – 40 с.

10. Термодинамические и теплофизические свойства продуктов сгорания. Справочник. / В.Е Алемасов, [и др.]; под ред. Академика В.П. Глушко. Т.3. М.: АН СССР, 1973. – 623 с.

Date: 2016-05-16; view: 755; Нарушение авторских прав