Ситуационная (практическая) задача № 1

При переносе грузов вертолетами используются тросы, которые изготовлены из синтетических материалов на основе химических технологий. В результате 25 испытаний троса на разрыв получены следующие данные:

2,948; 3,875; 5,526; 5,422; 4,409; 4,314; 5,150; 2,451; 5,226; 4,105; 3,280; 5,732; 3,249; 3,408; 7,204; 5,174; 6,222; 5,276; 5,853; 4,420; 6,525; 2,127; 5,264; 4,647; 5,591.

Необходимо:

§ Определить исследуемый признак и его тип (дискретный или непрерывный).

§ В зависимости от типа признака построить полигон или гистограмму относительных частот.

§ На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.

§ Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.

§ Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,01.

§ Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99.

§ С надежностью 0,95 проверить гипотезу о равенстве:

а) генеральной средней значению 5;

б) генеральной дисперсии значению 1.

Решение:

1. Тип признака непрерывный, т.к. исходные цифры могут принимать любые дробные значения на определенном промежутке.

Разобьем данные на 4 равных интервала:

Длина интервала

Интервал

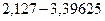
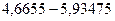
Гистограмма относительных частот

3. На основе анализа гистограммы распределения выдвигаем гипотезу о нормальном законе распределения исследуемого признака.

4. Среднее значение:

Дисперсия:

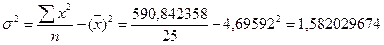
Среднее квадратическое (стандартное) отклонение:

5. Вводим гипотезы:

Исследуемый признак имеет нормальное распределение:

Исследуемый признак имеет другое распределение:

Условие принятия гипотезы

Вероятность попадания в интервалы:

Интервал
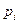
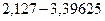
		0,1302	3,25	0,9363
		0,3396	8,49	0,2617
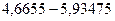
		0,3473	8,68	0,1998
		0,1393	3,48	0,0666
Сумма				1,4643

, следует гипотезу о нормальном распределении исследуемого признака принимаем.

6. Доверительный интервал для генерального среднего, при доверительной вероятности 99%:

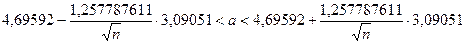
С вероятностью 99% генеральное среднее находится в интервале от до .

Доверительный интервал для генеральной дисперсии, при доверительной вероятности 99%:

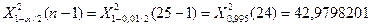
С вероятностью 99% генеральная дисперсия находится в интервале от до .

7а. Вводим гипотезы:

Условие принятия гипотезы

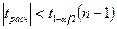
Условие принятия гипотезы выполняется , следует с вероятностью 95% генеральное среднее можно считать равным 5.

7б. Вводим гипотезы:

Условие принятия гипотезы

Условие принятия гипотезы выполняется , следует с вероятностью 95% генеральную дисперсию можно считать равным 1.

Date: 2016-05-16; view: 875; Нарушение авторских прав