
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ситуационная (практическая) задача №2
|
|
Ситуационная (практическая) часть.
Ситуационная (практическая) задача № 1.
При штамповке шариков для подшипников происходят случайные отклонения диаметров шариков от номинала. При обследовании 25 шариков эти отклонения составили:
| -0,530 | -0,207 | 0,025 | -0,238 | -0,132 | 0,216 | 0,087 | 0,162 | -0,462 | -0,442 |
| -0,441 | -0,163 | -0,525 | -1,163 | 0,510 | 0,316 | 0,057 | -0,402 | -0,371 | -0,351 |
| 0,111 | -0,161 | 0,521 | -0,551 | 0,152 | |||||
Необходимо:
1) Определить исследуемый признак и его тип (дискретный или непрерывный).
2) В зависимости от типа признака построить полигон или гистограмму относительных частот.
3) На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4) Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.
5) Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,05.
6) Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95.
7) С надёжностью 0,95 проверить гипотезу о равенстве:
а) генеральной средней значению 0,7;
б) генеральной дисперсии значению 0,16.
Решение.
1) Исследуемым признаком Х является отклонение диаметра шарика от номинала.
Объём выборки:
 .
.
Минимальное и максимальное значения признака в выборке:
 .
.
Размах выборки:
 .
.
Поскольку размах выборки значительно больше точности измерений (равна 0,001), то данный признак можно считать непрерывным.
2) Непрерывный признак графически изображается гистограммой относительных частот. Для построения гистограммы сначала построим статистический ряд распределе-ния выборки.
Определим количество интервалов по формуле Стерджесса:
 .
.
Примем число интервалов k = 6. Тогда величина одного интервала:
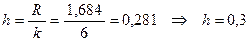 .
.
Статистический ряд распределения выборки представим в таблице 1.1:
Таблица 1.1
Номер интервала,
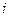
| Интервал,
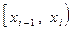
| Число значений,
попавших
в интервал

| Частота,

| Накопленная
частота,

| Частость,

|
| [-1,2; -0,9) | 0,04 | 0,04 | 0,133 | ||
| [-0,9; -0,6) | 0,00 | 0,04 | 0,000 | ||
| [-0,6; -0,3) | 0,36 | 0,40 | 1,200 | ||
| [-0,3; 0) | 0,20 | 0,60 | 0,667 | ||
| [0; 0,3) | 0,28 | 0,88 | 0,933 | ||
| [0,3; 0,6] | 0,12 | 1,00 | 0,400 | ||
| ∑ | [-1,2; 0,6] | 1,00 | − | − | |
Используя данные таблицы 1.1, построим гистограмму относительных частот.

3) На основе визуального анализа гистограммы выдвигаем гипотезу о нормальном распределении признака.
4) Для нахождения выборочных характеристик изучаемого признака составим расчётную таблицу (табл. 1.2):
Таблица 1.2
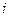
| 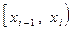
| 
| 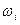
| 
| 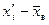
| 
| 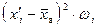
|
| [-1,2; -0,9) | -1,05 | 0,04 | -0,042 | -0,912 | 0,831744 | 0,033270 | |
| [-0,9; -0,6) | -0,75 | 0,00 | 0,000 | -0,612 | 0,374544 | 0,000000 | |
| [-0,6; -0,3) | -0,45 | 0,36 | -0,162 | -0,312 | 0,097344 | 0,035044 | |
| [-0,3; 0) | -0,15 | 0,20 | -0,030 | -0,012 | 0,000144 | 0,000029 | |
| [0; 0,3) | 0,15 | 0,28 | 0,042 | 0,288 | 0,082944 | 0,023224 | |
| [0,3; 0,6] | 0,45 | 0,12 | 0,054 | 0,588 | 0,345744 | 0,041489 | |
| ∑ | [-1,2; 0,6] | − | 1,00 | -0,138 | − | − | 0,133056 |
Среднее выборочное значение (5-й столбец, последняя строка):
 .
.
Выборочная дисперсия (8-й столбец, последняя строка):
 .
.
Исправленная выборочная дисперсия равна:
 .
.
Выборочное среднее квадратическое отклонение:

5) Проверим с помощью критерия согласия «хи-квадрат» Пирсона гипотезу о нормальном распределении признака Х. Уровень значимости α = 0,05.
Вычислим теоретические частоты по формуле:
 ,
,
где 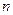 – объём выборки;
– объём выборки;
 ;
;
 – функция Лапласа.
– функция Лапласа.
Расчёты представим в таблице 1.3 (примем  и
и 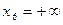 ).
).
Таблица 1.3
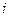
| 
| 
| 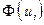
| 
| 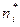
|
| -∞ | -∞ | -0,5000 | − | − | |
| -0,9 | -2,05 | -0,4797 | 0,0203 | 0,507 | |
| -0,6 | -1,24 | -0,3929 | 0,0869 | 2,172 | |
| -0,3 | -0,44 | -0,1684 | 0,2245 | 5,612 | |
| 0,37 | 0,1447 | 0,3131 | 7,827 | ||
| 0,3 | 1,18 | 0,3805 | 0,2358 | 5,895 | |
| +∞ | +∞ | 0,5000 | 0,1195 | 2,988 | |
Вычислим статистику  по выборочным данным:
по выборочным данным:
 .
.
Вычисления представим в таблице 1.4. Объединим интервалы 1, 2 и 3 и интервалы 5 и 6, чтобы выполнялось условие 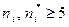 .
.
Таблица 1.4
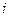
| 
| 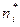
| 
| 
| 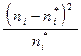
|
| 8,290 | 1,710 | 2,92362 | 0,353 | ||
| 7,827 | -2,827 | 7,98961 | 1,021 | ||
| 8,883 | 1,117 | 1,24709 | 0,140 | ||
| ∑ | 25,000 | − | − |  = 1,514 = 1,514
| |
Найдём по таблице распределения Пирсона критическое значение 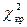 при уровне значимости
при уровне значимости  и числе степеней свободы
и числе степеней свободы  (здесь:
(здесь:  − число исходных интервалов;
− число исходных интервалов;  − число параметров, вычисленных по опытным данным):
− число параметров, вычисленных по опытным данным):
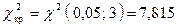 .
.
Так как  , то нет оснований отвергнуть гипотезу о нормальном распреде-лении случайной величины Х.
, то нет оснований отвергнуть гипотезу о нормальном распреде-лении случайной величины Х.
6) Доверительный интервал для генеральной средней m с доверительной вероятностью γ имеет вид:
 ,
,
где  – точность оценки (отклонение);
– точность оценки (отклонение);
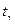 выбирается по таблице распределения Стьюдента для уровня значимости
выбирается по таблице распределения Стьюдента для уровня значимости  и числа степеней свободы
и числа степеней свободы  .
.
Найдём величину 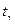 :
:
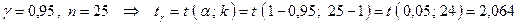 .
.
Рассчитаем точность оценки:
 .
.
Запишем доверительный интервал для генеральной средней:
 .
.
Таким образом, с вероятностью 0,95 среднее значение признака Х в генеральной совокупности будет лежать в интервале от -0,265 до -0,011.
Доверительный интервал для генеральной дисперсии σ2 с доверительной вероятностью γ имеет вид:
 ,
,
где  ,
, 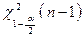 выбираются по таблице распределения Пирсона «хи-квадрат» для уровня значимости
выбираются по таблице распределения Пирсона «хи-квадрат» для уровня значимости  и числа степеней свободы
и числа степеней свободы  .
.
По условию задачи:
 .
.
Тогда:
 ,
,  .
.
По таблице распределения  находим значения квантилей:
находим значения квантилей:
 ,
, 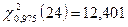 .
.
Найдём доверительный интервал для генеральной дисперсии:
 .
.
Таким образом, с вероятностью 0,95 дисперсия признака Х в генеральной совокупности будет лежать в интервале от 0,0912 до 0,2398.
7) С надёжностью 0,95 проверим гипотезу о равенстве генеральной средней значению 0,7.
Проверяемая гипотеза Н0:  .
.
Конкурирующая гипотеза Н1:  .
.
Ранее с надёжностью 0,95 построен доверительный интервал для 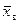 :
:
 .
.
Так как значение  не принадлежит этому интервалу, то гипотеза Н0 отвергается.
не принадлежит этому интервалу, то гипотеза Н0 отвергается.
С надёжностью 0,95 проверим гипотезу о равенстве генеральной дисперсии значению 0,16.
Проверяемая гипотеза Н0:  .
.
Конкурирующая гипотеза Н1:  .
.
Ранее с надёжностью 0,95 получен доверительный интервал для  :
:
 .
.
Так как значение  принадлежит этому интервалу, то с надёжностью 0,95 гипотеза Н0 принимается.
принадлежит этому интервалу, то с надёжностью 0,95 гипотеза Н0 принимается.
Ответ:
1) Исследуемый признак непрерывный.
3) Предполагаемое распределение признака – нормальное.
4)  ,
,  ,
, 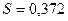 .
.
5) Гипотеза о нормальном распределении принимается на уровне значимости 0,05.
6) Доверительные интервалы с вероятностью 0,95:
 и
и  .
.
7) С надёжностью 0,95 гипотезу о равенстве генеральной средней значению 0,7 отвергаем, а гипотезу о равенстве генеральной дисперсии значению 0,16 принимаем.
Ситуационная (практическая) задача №2.
В цехе с 10 станками ежедневно регистрировалось число вышедших из строя станков. Всего было проведено 200 наблюдений, результаты которых приведены ниже:
| Число выбывших станков | |||||||||||
| Число зарегистрированных случаев | |||||||||||
Необходимо:
1) Определить исследуемый признак и его тип (дискретный или непрерывный).
2) В зависимости от типа признака построить полигон или гистограмму относительных частот.
3) На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.
4) Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.
5) Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,99.
6) При уровне значимости 0,05 проверить гипотезу о том, что число выбывших из строя станков имеет распределение Пуассона.
Решение.
1) Исследуемым признаком Х является число вышедших из строя станков из 10. Это дискретный признак.
2) Дискретный признак графически изображается полигоном относительных частот. Для построения полигона сначала построим статистический ряд распределения выборки объёмом  (таблица 2.1):
(таблица 2.1):
Таблица 2.1
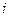
| Значение
признака,

| Частота,

| Частота,

| Накопленная
частота,

|
| 0,175 | 0,175 | |||
| 0,315 | 0,490 | |||
| 0,235 | 0,725 | |||
| 0,120 | 0,845 | |||
| 0,085 | 0,930 | |||
| 0,040 | 0,970 | |||
| 0,020 | 0,990 | |||
| 0,010 | 1,000 | |||
| 0,000 | 1,000 | |||
| 0,000 | 1,000 | |||
| 0,000 | 1,000 | |||
| ∑ | − | 1,000 | − | |
Используя данные таблицы 2.1, построим полигон относительных частот.

3) На основе визуального анализа полигона выдвигаем гипотезу о распределении признака по закону Пуассона:
 .
.
4) В случае случайной величины Х, имеющей распределение Пуассона, имеет смысл оценивать параметр λ, поскольку он определяет числовые характеристики:
 .
.
Определим точечную оценку λ* параметра λ, используя метод правдоподобия.
Составим функцию правдоподобия для случайной величины Х:

где  – наблюдаемые значения случайной величины.
– наблюдаемые значения случайной величины.
Для удобства дальнейших вычислений прологарифмируем функцию правдоподобия:

Найдём значение λ*, при котором функция правдоподобия принимает максималь-ное значение:
 ;
;
 ;
;
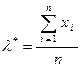 .
.
Рассчитаем оценку параметраλ по найденной формуле (поскольку у нас уже сгруппированный ряд, то используем формулу средней арифметической взвешенной):
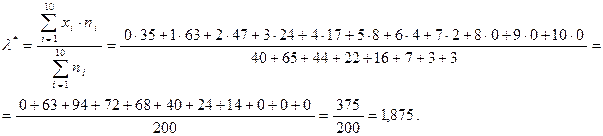
5) Построим доверительный интервал для параметра λ. Он имеет вид:
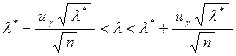 ,
,
где 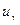 выбирается по таблице Лапласа для доверительной вероятности
выбирается по таблице Лапласа для доверительной вероятности  .
.
Найдём величину 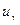 :
:
 .
.
Рассчитаем доверительный интервал:
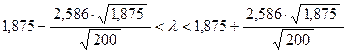 ;
;


 .
.
Таким образом, с вероятностью 0,99 параметр λ признака Х в генеральной совокупности будет лежать в интервале от 1,625 до 2,125.
6) Проверим с помощью критерия согласия «хи-квадрат» Пирсона гипотезу о распределении признака Х по закону Пуассона. Уровень значимости α = 0,05.
Сначала вычислим теоретические частоты по формуле:
 ,
,
где  ;
;
 – объём выборки;
– объём выборки;
 – оценка параметра.
– оценка параметра.
Затем найдём статистику  по выборочным данным:
по выборочным данным:
 .
.
Расчёты представим в таблице 2.2 (объединим значения 6, 7, 8, 9 и 10, чтобы выполнялось условие 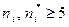 ).
).
Таблица 2.2
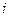
| 
| 
| 
| 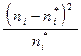
|
| 0,153355 | 30,6710 | 0,611 | ||
| 0,287541 | 57,5081 | 0,524 | ||
| 0,269569 | 53,9139 | 0,887 | ||
| 0,168481 | 33,6962 | 2,790 | ||
| 0,078975 | 15,7951 | 0,092 | ||
| 0,029616 | 5,9232 | 0,728 | ||
| 0,012459 | 2,4917 | 4,939 | ||
| ∑ | − | − |  = 10,571 = 10,571
| |
Найдём по таблице распределения Пирсона критическое значение 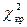 при уровне значимости
при уровне значимости  и числе степеней свободы
и числе степеней свободы  (здесь:
(здесь:  − число интервалов в таблице 2.2;
− число интервалов в таблице 2.2;  − число параметров, вычисленных по опытным данным):
− число параметров, вычисленных по опытным данным):
 .
.
Так как  , то нет оснований отвергнуть гипотезу о распределении случайной величины Х по закону Пуассона.
, то нет оснований отвергнуть гипотезу о распределении случайной величины Х по закону Пуассона.
Ответ:
1) Исследуемый признак дискретный.
3) Предполагаемое распределение признака – распределение Пуассона.
4)  .
.
5) Доверительный интервал с вероятностью 0,99:  .
.
6) Гипотеза о распределении Пуассона принимается на уровне значимости 0,05.
Тестовые задания.
1. Из генеральной совокупности извлечена выборка.
| хi | |||||||
| рi | |||||||
Найти относительную частоту варианты x6 = 7.
А. 50
Б. 4
В. 1
Г. 0,08
Решение.
Объём выборки:
 .
.
Относительная частота варианты x6 = 7:
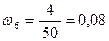 .
.
Правильный ответ – Г.
2. Дана выборка 2, 4, 5, 5, 10, 2, 7, 8, 9, 8. Найти несмещённую оценку математического ожидания.
А. 60
Б. 4
В. 5
Г. 6
Решение.
Несмещённая оценка математического ожидания:
 .
.
Правильный ответ – Г.
3. Мода вариационного ряда 1, 2, 3, 3, 5, 6, 6, 6, 7, 8 равна:
А. 8
Б. 6
В. 4,5
Г. 4,7
Решение.
Мода – признак с наибольшей частотой:
 .
.
Правильный ответ – Б.
4. Дана выборка 9, 4, 5, 5, 4, 2, 9, 7, 6, 9. Найти выборочную дисперсию.
А. 6
Б. 5,4
В. 4
Г. 50
Решение.
Выборочная средняя:
 .
.
Выборочная дисперсия:
 .
.
Правильный ответ – Б.
5. Дана выборка 9, 4, 5, 7, 4, 2, 10, 7, 5, 7. Найти несмещённую оценку дисперсии.
А. 8
Б. 5,4
В. 7,2
Г. 6
Решение.
Выборочная средняя:
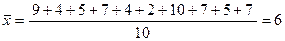 .
.
Выборочная дисперсия:
 .
.
Исправленная выборочная дисперсия (несмещённая оценка дисперсии):
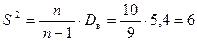 .
.
Правильный ответ – Г.
6. Дан доверительный интервал (16,5; 17,25) для оценки математического ожидания нормального распределённого количественного признака. Тогда точечная оценка математического ожидания равна:
А. 16,5
Б. 17,25
В. 0,375
Г. 16,88
Решение.
Доверительный интервал для оценки математического ожидания нормального распределённого количественного признака симметричен относительно точечной оценки  математического ожидания:
математического ожидания:
 .
.
Тогда точечная оценка математического ожидания равна:
 .
.
Правильный ответ – Г.
7. Дан доверительный интервал (16,3; 17,34) для оценки математического ожидания нормального распределённого количественного признака. Тогда точность оценки равна.
А. 16,82
Б. 0,52
В. 0,55
Г. 0,05
Решение.
Доверительный интервал для оценки математического ожидания:
 .
.
Точечная оценка математического ожидания равна:
 .
.
Тогда точность оценки:
 .
.
Правильный ответ – Б.
8. Чему равен квантиль распределения «хи-квадрат»  ?
?
А. 10,473
Б. 28,214
В. 20,951
Г. 30,813
Решение.
По таблице распределения «хи-квадрат» находим:
 .
.
Правильный ответ – Г.
9. Чему равен квантиль распределения Стьюдента 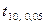 ?
?
А. 3,1693
Б. 2,7638
В. 0,1693
Г. -3,1693
Решение.
По таблице распределения Стьюдента находим:
 .
.
Правильный ответ – Б.
10. Соотношением вида P(K>2,01) = 0,01 можно определить:
А. правостороннюю критическую область
Б. левостороннюю критическую область
В. область принятия гипотезы
Г. двустороннюю критическую область
Правильный ответ – А.
| <== предыдущая | | | следующая ==> |
| Интеграция Украины в мировое сообщество: современные тенденции | | | Правописание гласных букв и, ы в корне слова |
Date: 2016-05-16; view: 1292; Нарушение авторских прав