Описание машины Тьюринга

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j→q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_j записывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <q_i, a_j> имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

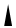
2.Доказать, что если формулы Ф дизъюнкция ψ и ˅Ф тавтологии, то и формула ˅ψ – тавтология.

Билет№10

1.Гиперкуб как область определения булевой функции. Его элементы.

Рассмотренное отношение порядка на будем называть булевым порядком.

Булев куб как упорядоченное множество, можно изобразить в виде диаграммы Хассе. На рис. 6.1 приведены диаграммы Хассе для булевых кубов размерностей от 0 до 4.

Другой способ наглядного изображения булева куба основан на том, что диаграмма Хассе любого конечного упорядоченного множества может быть задана в виде ориентированной сети, так что дуга из вершины, сопоставленной элементу 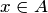, ведет в вершину, сопоставленную элементу , тогда и только тогда, когда доминирует над и каждый уровень сети состоит из вершин, сопоставленных попарно несравнимым элементам множества (т.е. элементам некоторой антицепи в ). Входы сети сопоставлены минимальным, а выходы — максимальным элементам .

Каждый уровень представляющей булев куб сети состоит из всех вершин, соответствующих наборам, у которых ровно компонент отличны от нуля (множество всех таких наборов для фиксированного называют k-слоем булева куба ).

Сеть, служащую изображением булева куба размерности , будем называть булевой n-сетъю или просто булевой сетью, если упоминание о размерности опускается. Так как булев куб имеет наименьший элемент — нулевой набор и наибольший элемент — единичный набор, то каждая булева сеть имеет единственный вход (помеченный нулевым набором) и единственный выход (помеченный единичным набором).

На рис. 6.2 приведено изображение булева куба в виде сети.

Помимо булева порядка полезно также ввести на булевом кубе другое отношение порядка, которое мы будем называть лексикографическим порядком, используя обозначение .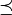

Пусть (для произвольного фиксированного ). По определению, , если

Каждая из сумм в неравенстве (6.2) есть не что иное, как представление некоторого натурального числа (включая и нуль) в двоичной системе счисления (при числе разрядов, равных фиксированной размерности ). На каждый булев вектор можно смотреть как на такое представление (двоичный код) натурального числа, и лексикографический порядок на булевом кубе есть не что иное, как естественный числовой порядок на подмножестве множества (при условии, что числа заданы в двоичной системе счисления). Более строго: упорядоченное множество изоморфно подмножеству с естественным числовым порядком.

Заметим, что отношение лексикографического порядка является, в отличие от булева порядка, отношением линейного порядка.

Пример 6.2. Набор как двоичный код числа лексикографически больше набора , служащего двоичным кодом числа 3, но при этом указанные наборы не сравнимы по отношению булева порядка.

Однако лексикографический порядок при изучении булевых кубов играет вспомогательную роль. В частности, при изображении булевых кубов (в виде диаграмм Хассе или в виде сети) принято располагать вершины каждого k-слоя в лексикографическом порядке (по возрастанию — слева направо или сверху вниз). Везде в дальнейшем, рассуждая о булевом кубе как об упорядоченном множестве, мы имеем в виду булев порядок.

2.Определение отношений:R^-1;отрицание R;I;U;

Билет №11

1.Булева функция n переменных.

Булева функция (или логическая функция, или функция алгебры логики) от n аргументов — в дискретной математике — отображение Bⁿ → B, где B = {0,1} — булево множество. Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения (n -я прямая степень) Bⁿ называют булевыми векторами. Множество всех булевых функций от любого числа аргументов часто обозначается P ₂, а от n аргументов — P ₂(n). Переменные, принимающие значения из булева множества называются булевыми переменными ^[2]. Булевы функции названы по фамилии математика Джорджа Буля.

При работе с булевыми функциями происходит полное абстрагирование от содержательного смысла, который имелся в виду в алгебре высказываний^[2]. Тем не менее, между булевыми функциями и формулами алгебры высказываний можно установить взаимно-однозначное соответствие, если^[3]:

· установить взаимно-однозначное соответствие между булевыми переменными и пропозициональными переменными,

· установить связь между булевыми функциями и логическими связками,

· оставить расстановку скобок без изменений.

2.Привидите пример рефлексивного, симметричного, транзитивного отношения.

Рефлексивное:

· отношения эквивалентности:

· отношение равенства

· отношение сравнимости по модулю

· отношение параллельности прямых и плоскостей

· отношение подобия геометрических фигур;

· отношения нестрогого порядка:

· отношение нестрогого неравенства

· отношение нестрогого подмножества

· отношение делимости

Симметричного:

§ Отношения эквивалентности:

§ отношение равенства

§ отношение сравнимости по модулю

§ отношение равномощности множеств

§ отношение параллельности прямых и плоскостей

§ отношение подобия геометрических фигур

§ Отношения толерантности:

§ отношение "знакомства"

§ отношение "наличие общего свойства"

Транзитивного:

§ Отношения частичного порядка:

§ строгое неравенство

§ нестрогое неравенство

§ включение подмножества:

§ строгое подмножество

§ нестрогое подмножество

§ делимость:

§

§

§ Равенство

§ Эквивалентность

§ Импликация

§ Параллельность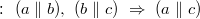

§ Отношение подобия геометрических фигур

§ Являться предком

Билет №12

1.Определения бинарных отношений. Свойство: функциональность, тотальность, инъективность, сюръективность.

СМ.Билет №6 вопрос 2, билет №3 1 вопрос.

2.Виды множества. Способы задания. Мощность множества.

СМ. Билет №2 1 вопрос

Билет №13

1.Великие учёные, которые внесли вклад в развитие математической логики (не менее 5 перечислить; о двоих по выбору рассказать подробно.)

См. Билет №3 вопрос 2

2.Машина Тьюринга

См. Билет №1 Вопрос 2

Билет №14

1. Декартово произведение множеств.

См. Билет №8 1 вопрос

2. См. билет №8 2 вопрос

Билет №15

1.Высказывание, свойство, отношение, тернарное отношение. Запись с помощью предикатов.

Высказывание — предложение, выражающее суждение. Если суждение, составляющее содержание (смысл) некоторого высказывания, истинно, то и о данном высказывании говорят, что оно истинно. Сходным образом ложным называют такое высказывание, которое является выражением ложного суждения. Истинность и ложность называются логическими, или истинностными, значениями высказываний.

Высказывание должно быть повествовательным предложением. Высказывания обычно противопоставляются повелительным, вопросительным и любым другим предложениям, оценка истинности или ложности которых невозможна.

Тернарное отношение — то же, что трёхместное отношение (трёхчленное отношение).

p, q, r, s, p ₁... – пропозициональные переменные (символы для обозначения целых повествовательных предложений);

a, b, c, d, a ₁... – предметные константы (символы для обозначения единичных имен);

x, y, z, x ₁... – предметные переменные (символы для обозначения общих имен);

P, Q, R, S, P ₁... – предикатные символы (символы для обозначения свойств и отношений);

ù - логическое отрицание («не» или «неверно, что»);

Ù - конъюнкция («и»);

Ú - дизъюнкция («или»);

Ú - строгая дизъюнкция («либо…, либо…»);

É - импликация («если…, то…»);

º - тождество (эквивалентность) («тогда и только тогда, когда…»);

" - квантор всеобщности («все», «каждый»);

$ - квантор существования («некоторые», «существуют»);

Помимо этого в записи используются технические знаки: скобки и запятая.

Выражения языка логики предикатов называются формулами. Определению правильно построенной формулы предшествует определение терма.

2.Дедукция и индукция в широком смысле.

Дедукция (лат. deductio — выведение) — метод мышления, следствием которого является логический вывод, в котором частное заключение выводится из общего. Цепь умозаключений (рассуждений), где звенья (высказывания) связаны между собой логическими выводами.

Началом (посылками) дедукции являются аксиомы или просто гипотезы, имеющие характер общих утверждений («общее»), а концом — следствия из посылок, теоремы(«частное»). Если посылки дедукции истинны, то истинны и её следствия. Дедукция — основное средство доказательства. Противоположно индукции.

Пример простейшего дедуктивного умозаключения:

1. Все люди смертны.

2. Сократ — человек.

3. Следовательно, Сократ смертен.

Индукция (из лат. inductio «выведение, наведение») — широко используемый в науке термин.

В логике

· Индуктивное умозаключение — метод рассуждения от частного к общему.

· Полная индукция — метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности.

· Неполная индукция — наблюдения за отдельными частными случаями наводит на гипотезу, которая нуждается в доказательстве.

· Математическая индукция — метод доказательства для последовательности натуральных чисел либо объектов, однозначно занумерованных натуральными числами.

Билет №16

1.Понятие алгоритма. Алгоритм Евклида.

Алгоритм — набор инструкций, описывающих порядок действий исполнителя для достижения некоторого результата. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.

Ранее в русском языке писали «алгори ф м», сейчас такое написание используется редко, но, тем не менее, имеет место исключение (нормальный алгорифм Маркова).

Часто в качестве исполнителя выступает компьютер, но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек (а может быть и некоторый механизм, ткацкий станок, и пр.).

Можно выделить алгоритмы вычислительные (о них в основном идет далее речь), и управляющие. Вычислительные по сути преобразуют некоторые исходные данные в выходные, реализуя вычисление некоторой функции. Семантика управляющих алгоритмов существенным образом может отличаться и сводиться к выдаче необходимых управляющих воздействий либо в заданные моменты времени, либо в качестве реакции на внешние события (в этом случае, в отличие от вычислительного алгоритма, управляющий может оставаться корректным при бесконечном выполнении).

Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако в явном виде понятие алгоритма сформировалось лишь в начале XX века.

Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений^[1] или «эффективного метода»^[2]; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга. В методологии алгоритм является базисным понятием и получает качественно новое понятие как оптимальности по мере приближения к прогнозируемому абсолюту. В современном мире алгоритм в формализованном выражении составляет основу образования на примерах, по подобию.

Алгоритм Евклида — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел (или общей меры двух отрезков). Алгоритм назван в честь греческого математика Евклида, который впервые описал его в VII и X книгах «Начал». В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары.

Первое описание алгоритма находится в «Началах» Евклида (около 300 лет до н. э.), что делает его одним из старейших численных алгоритмов, используемых в наше время. Оригинальный алгоритм был предложен только для натуральных чисел и геометрических длин (вещественных чисел). Однако в XIX веке он был обобщён на другие типы чисел, такие как целые числа Гаусса и полиномы от одной переменной. Это привело к появлению в современной общей алгебре такого понятия, как евклидово кольцо. Позже алгоритм Евклида также был обобщён на другие математические структуры, такие как узлы и многомерные полиномы.

Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA^[4], широко распространённого вэлектронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений^[5], при построении непрерывных дробей, в методе Штурма. Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например таких кактеорема Лагранжа о сумме четырёх квадратов и основная теорема арифметики.

2.Бинарные отношения, их виды и свойства. Связь с графами.

Билет №6 вопрос 2

Билет №17

1.Конъюнкция, дизъюнкция, импликация, отрицание.

Билет 8 Вопрос 2

Отрицание в логике — унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком перед или чертой -- над суждением. Синоним: логическое "НЕ".

Как в классической, так и в интуиционистской логике «двойное отрицание» A является следствием суждения A, то есть имеет место тавтология: .

Обратное утверждение верно в классической логике (закон двойного отрицания), но не имеет места в интуиционистской. То есть, отрицание отрицания искомого утверждения не может служить интуиционистским доказательством, в отличие от классической логики. Это различие двух логических систем обычно полагается главным.

Основная статья: Логические элементы — отрицание

Мнемоническое правило для отрицания звучит так: На выходе будет:

· «1» тогда и только тогда, когда на входе «0»,

· «0» тогда и только тогда, когда на входе «1».

2.Кванторные операции.

Пусть имеется предикат P (x), определенный на множестве M и . Подставим a вместо x в предикат P (x), получим высказывание P (a), которое называется единичным. Наряду с образованием из предикатов единичных высказываний рассмотрим еще две операции, которые преобразуют одноместный предикат в высказывание.

1. Квантор всеобщности.

Пусть P (x) – предикат, определенный на множестве M. Под выражением понимают высказывание, истинное, когда P (x) истинно для каждого элемента и ложное в противном случае. Это высказывание не зависит от x. Соответствующее ему словесное выражение «Для всякого x P (x) истинно». Символ называется квантором всеобщности. Переменную x в предикате P (x) называют свободной (ей можно придавать различные значения из M), в высказывании переменную x называют связанной квантором всеобщности.

2. Квантор существования.

Пусть P (x) – предикат, определенный на множестве M. Под выражением понимают высказывание, которое является истинным, если существует элемент , для которого P (x) истинно и ложным в противном случае. Это высказывание не зависит от x. Соответствующее ему словесное выражение «существует x, при котором P (x) истинно». Символ называется квантором существования.

Пример.

M=N, P (x) – «число x кратно 5»;

– «Все натуральные числа кратны 5» ложно, т.е. ;

– «Существует натуральное число, кратное 5» истинно, то есть .

Замечание 1. Высказывание истинно только в том единственном случае, когда P (x) тождественно истинный предикат, а высказывание ложно только в том единственном случае, когда P (x) тождественно ложный предикат.

Замечание 2. Кванторные операции применяются и к многоместным предикатам. Пусть, например, на множестве M задан двухместный предикат P (x, y). Применение кванторной операции к предикату P (x, y) по переменной x ставит в соответствие двухместному предикату P (x, y) одноместный предикат (или одноместный предикат ) [для любого xP (x, y) истинно (существует x, при котором P (x, y) истинно)], зависящий от переменной y и не зависящий от переменной x. К ним можно применить кванторные операции по переменной y, которые приведут к высказываниям следующих видов: ; ; ; ; ; ; ; .

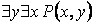Пример.

Рассмотрим предикат P (x, y) – «y является делителем x», определенный на множестве N. Применение кванторных операций к этому предикату приводит к 8 возможным высказываниям:

1) – «Для всякого y и для всякого x, y является делителем x»;

2) – «Существует y, которое является делителем всякого x»;

3) – «Для всякого y существует x такое, что x делится на y»;

4) 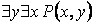– «Существует y и существует x такие, что y является делителем x»;

5) – «Для всякого x и для всякого y, y является делителем x»;

6) – «Для всякого x существует y такое, что x делится на y»;

7) – «Существует x такое, что для всякого y, x делится на y»;

8) – «Существует x и существует y такие, что y является делителем x».

Высказывания 1), 5), 7) ложны; а высказывания 2), 3), 4), 6), 8) истинны.

Билет № 18

1.Теорема о мощности декартова произведения множества. Степень множества.

Пусть - конечные множества. Соответственно мощности этих множеств равны: .

Тогда мощность прямого произведения множеств равна произведению мощностей соответствующих множеств, т.е. .

Доказательство методом математической индукции.

Для 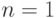теорема тривиально верна. Предположим, что она верна и для и докажем ее справедливость для .

По предположению . Возьмем любой вектор из и припишем справа элемент . Это можно сделать способом, т. е. получим различных векторов из .

Таким образом, из всех векторов приписыванием справа элемента из можно получить векторов, причем все они различны. Поэтому для теорема верна и, следовательно, верна для любых .

Следствие:

Булеан (степень множества, показательное множество, множество частей) — множество всех подмножеств данного множества , обозначается или 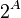(так как оно соответствует множеству отображений из в ).

Если два множества равномощны, то равномощны и их булеаны. Обратное утверждение (то есть инъективность операции для кардиналов) является независимым от ZFC.

В категории множеств можно снабдить функцию структурой ковариантного или контравариантного функтора следующим образом:

· ковариантный функтор отображает функцию в функцию такую, что она отображает в образ относительно ;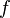

· контравариантный функтор отображает функцию в такую, что она отображает в полный прообраз относительно .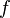

2.Основные логические операции.

Билет 8 вопрос 2

Билет №19

1.Машина Тьюринга

Билет 1, 2 вопрос

2.Доказать

Билет №20

1.Гиперкуб как область определения булевой функции. 0- мерный, 1- мерный,2- мерный, 3- мерный единичный куб.

Билет 10, вопрос 1.

Date: 2016-05-15; view: 570; Нарушение авторских прав