Примеры моделей линейного программирования

Ниже будут рассмотрены несколько ситуаций, исследование которых возможно с применением средств линейного программирования. Так как основным показателем в этих ситуациях является экономический— стоимость, то соответствующие модели являются экономико-математическими.

Задача о раскрое материалов. На обработку поступает материал одного образца в количестве d единиц. Требуется изготовить из него к разных комплектующих изделий в количествах, пропорциональных числам а₁,..., а_к. Каждая единица материала может быть раскроена n различными способами, при этом использование i-го способа (i=1,…,n) дает b_ij, единиц j-го изделия (j = 1,...,k).

Требуется найти план раскроя, обеспечивающий максимальное число комплектов.

Экономико-математическая модель этой задачи может быть сформулирована следующим образом. Обозначим x_i — число единиц материалов, раскраиваемых i-м способом, и x — число изготавливаемых комплектов изделий.

Учитывая, что общее количество материала равно сумме его единиц, раскраиваемых различными способами, получим:

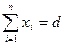(1)

Условие комплектности выразится уравнениями:

(j=1,…,k)(2)

Очевидно, что

x_i 0 (i=1,…,n)(3)

Целью является определить такое решение Х= (x₁,…,x_n), удовлетворяющее ограничениям (1)-(3), при котором функция F = x принимает максимальное значение. Проиллюстрируем рассмотренную задачу следующим примером Для изготовления брусьев длиной 1,5 м, 3 м и 5 м в соотношении 2:1:3 на распил поступают 200 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Чтобы сформулировать соответствующую оптимизационную задачу линейного программирования, определим все возможные способы распила бревен, указав соответствующее число получаемых при этом брусьев (табл. 1).

Таблица 1

Обозначим через x_i — число бревен, распиленных i-м способом (i = 1.2, 3, 4); х —число комплектов брусьев.

С учетом того, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, оптимизационная экономико-математическая модель примет следующий вид

х → max

при ограничениях:

x₁ +x₂ +x₃ +x₄ =200

4x₁ +2x₂ =2x

x₂ +2x₃ =x

x₄ =2x

x_i 0 (i=1,2,3,4)

Задача выбора оптимальной производственной программы предприятия. Пусть предприятие может выпускать n различных видов продукции. Для выпуска этих видов продукции предприятие использует М видов материально-сырьевых ресурсов и N видов оборудования. Необходимо определить объемы производства предприятия (т.е. его производственную программу) на заданном интервале планирования [0, Т], чтобы максимизировать валовую прибыль предприятия.

Далее будем полагать, что валовая прибыль есть выручка, полученная от реализации продукции за вычетом условно-постоянных и переменных затрат. Иными словами, необходимо максимизировать целевую функцию вида:

(4)

где a_i — цена реализации продукции вида i;

b_i — переменные затраты на выпуск одной единицы продукции вида i;

Zp — условно постоянные затраты, которые будем предполагать независимыми от вектора х = (x₁,..., x_n).

При этом должны быть выполнены ограничения на объемы используемых материально-сырьевых ресурсов и время использования оборудования на интервале [0,T].

Обозначим через Lj(j = l,...,M) объем запасов материально-сырьевых ресурсов вида j, а через τ_k (k = 1,..., N) — время, в течение которого может быть использовано оборудование вида k. Известно потребление материально-сырьевых ресурсов вида j на выпуск одной единицы продукции вида i, которое обозначим через l_ij (i = 1,..., n; j = 1,...,М). Известно также t_ik — время загрузки одной единицы оборудования вида k изготовления одной единицы продукции вида i (i = 1,..., n; k = 1,..., N). Через m_k обозначим количество единиц оборудования вида k (k=l,...,N).

При введенных обозначениях ограничения на объем потребляемых материально-сырьевых ресурсов могут быть заданы таким образом:

(j=1,…,M)(5)

Ограничения на производственные мощности задаются следующими неравенствами

k=1,…,N(6)

Кроме того, переменные

x_i ≥0 i=1,…,n (7)

Таким образом, задача выбора производственной программы, максимизирующей прибыль, заключается в выборе такого плана выпуск х = (х₁...,х_n), который удовлетворял бы ограничениям (5)-(7) и максимизировал бы функцию (4).

В некоторых случаях предприятие должно поставить заранее оговоренные объемы продукции Vt другим хозяйствующим субъектам и тогда в рассматриваемой модели вместо ограничения (1.7) может быть включено ограничение вида:

x_t > Vt i= 1,...,n.

Задача о диете. Рассмотрим задачу составления душевого рациона питания минимальной стоимости, которое бы содержало определенные питательные вещества в необходимых объемах. Будем предполагать, что имеется известный перечень продуктов из n наименований (хлеб, сахар, масло, молоко, мясо и т.д.), которые мы будем обозначать буквами F₁,...,F_n. Кроме того, рассматриваются такие характеристики продуктов (питательные вещества), как белки, жиры, витамины, минеральные вещества и другие. Обозначим эти компоненты буквами N₁,...,N_m. Предположим, что для каждого продукта F_i известно (i = 1,...,n) количественное содержание в одной единице продукта указанных выше компонент. В этом случае можно составить таблицу, содержащую характеристику продуктов:

F₁,F₂,…F_j …F_n

_____________

N₁ a₁₁ a₁₂ …a_1j …a_1N

N₂ a₂₁ a₂₂ …a_2j …a_2N

N_i a_i1 a_i2 …a_ij …a_iN

N_m a_m1 a_m2 …a_mj …a_mN

Элементы этой таблицы образуют матрицу, имеющую m строк и n столбцов. Обозначим ее через A и назовем матрицей питательности. Предположим, что мы составили рацион х = (х₁,x₂,...,х_n) на некоторый период (например, месяц). Иными словами, мы планируем каждому человеку на месяц х, единиц (килограммов) продукта F₁,x₂ единиц продукта F₂ и т.д. Нетрудно вычислить, какое количество витаминов, жиров, белков и прочих питательных веществ получит человек за этот период. Например, компонента N₁ присутствует в этом рационе в количестве

a₁₁ x₁ + a₁₂ x_2+…+ a_1n x_n

поскольку согласно условию в x₁ единицах продукта F₁ согласно матрице питательности содержится a₁₁ x₁ единиц компоненты N₁; к этому количеству добавляется порция а₁₂ x₂ вещества N₁ из х₂ единиц продукта F₂ и т.д. Аналогично можно определить и количество всех остальных веществ N_i в составляемом рационе (х₁,..., х_n).

Допустим, что имеются определенные физиологические требования, касающиеся необходимого количества питательных веществ в N_i (i/ = 1,..., N) в планируемый срок. Пусть эти требования заданы вектором b = (b₁...,b_n), i-я компонента которого b_i указывает минимально необходимое содержание компонента N_i в рационе. Это означает, что коэффициенты x_i вектора х должны удовлетворять следующей системе ограничений:

a₁₁ x₁ + a₁₂ x_2+…+ a_1n x_n ≥b₁

a₂₁ x₁ + a₂₂ x_2+…+ a_2n x_n ≥b₂ (8)

a_m1 x₁ + a_m2 x_2+…+ a_mn x_n ≥b_m

Кроме того, из содержательного смысла задачи очевидно, что все переменные х₁,...,х_n неотрицательны и поэтому к ограничениям (8) добавляются еще неравенства

x₁ ≥0; x₂ ≥0;… x_n ≥0; (9)

Учитывая, что в большинстве случаев ограничениям (8) и (9) удовлетворяет бесконечно много рационов, выберем тот из них, стоимость которого минимальна.

Пусть цены на продукты F₁,...,F_n равны соответственно с₁,…,c_n

Следовательно, стоимость всего рациона х = (х₁..., х_n) может быть записана в виде

c₁ x₁ + c₂ x₂ +…+ c_n x_n →min (10)

Окончательно формулировка задачи о диете заключается в том, чтобы среди всех векторов х = (x₁,...,х_n) удовлетворяющих ограничениям (8) и (9) выбрать такой, для которого целевая функция (10) принимает минимальное значение.

Транспортная задача. Имеется m пунктов S₁,..., S_m производства однородного продукта (угля, цемента, нефти и т.п.), при этом объем производства в пункте S_i равен a_i единиц. Произведенный продукт потребляется в пунктах Q₁...Q_n и потребность в нем в пункте Q_j составляет k_j единиц (j = 1,...,n). Требуется составить план перевозок из пунктов S_i (i = 1,...,m) в пункты Q_j (j = 1,..., n), чтобы удовлетворить потребности в продукте b_j, минимизировав транспортные расходы.

Пусть стоимость перевозок одной единицы продукта из пункта S_i в пункт Q_i равна c_ij. Будем далее предполагать, что при перевозке х_ij единиц продукта из S_i в Q_j транспортные расходы равны c_ij x_ij.

Назовем планом перевозок набор чисел х_ij c_i = 1,..., m; j = 1,..., n, удовлетворяющий ограничениям:

x_ij ≥0, i=1,2,…,m; j=1,…,n (11)

Содержательный смысл уравнений (11) состоит в том, что из пункта S_i при плане х_ij вывозится во все пункты Q_j объем , который должен быть равен запасу a_i. В пункт Q_j поступает из всех пунктов S_i суммарное количество продукта, которое в точности должно быть равно потребности b_j.

При плане перевозок (х_ij) транспортные расходы составят величину

(12)

Окончательное формирование транспортной задачи таково: среди всех наборов чисел (х_ij), удовлетворяющих ограничениям (11), найти набор, минимизирующий (12).