Описание 3-х массового 5 page

Необходимо: синтезировать закон (2), то есть найти значение матрицы С1(n, m) – число из условия воспроизведения задано = функции Y0 в соответствии с требованием функционала (4).

х0 – вектор ненулевых начальных условий.

х

.

Дв х

..

z1 Iр х

z2

z3

Н

.

z1 1 0 0 x

..

z2 = 0 1 0 x

z3 0 0 1 Iя

Матрица Н характеризует структуру измерительной системы

.

1 0 0 х

..

[C1, C2, C3]т = 0 1 0 х

0 0 1 Iя

...

[C1x+C2x+C3Iя]=[x]

Находим коэффициенты по всем обратным связям.

Y-выход системы.

Y=[q1,q2,...,qn][x1,x2,...,xn]=q1x1+q2x2...qnxn

Показывает, какие фазовые координаты входят в выход системы.

[Q]=[00000010]

седьмая координата- выходная фазовая координата.

(г) – уравнение закона управления, которое обеспечивает движению (1) заданные характеристики.

Задача заключается в выборе структуры (2) и параметров (2) по заданной характеристике.

X3-Y0 – сигнал ошибки.

mò(x3-Y0)dt } ПИД

1(t) x3 e

m/p V объект

Y0

n сих Q

Y0 – главный выходной сигнал.

Степень приближения процесса к хорошему оценивается функционалом (4).

J=ò(K1d2+K2d2+K3d2)dt

.

x1=a11x1+a12x2+a13x3+bV

.

x2=a21x1+a22x2+a23x3+b2V (**)

.

x3=a31x1+a32x2+a33x3+b3V

x3=1=D0+Dk sin

Y=q1x1+q2x2+q3x3

V=cux+n(x3-Y0)+mò(Y3-Y0)dt

Если мы управляющее воздействие V, x – фаз координируем, х3 и Y0 подставим в уравнение в форме тригонометрических рядов, то получим систему

n n

Рк cos+Tk sin = SCiAik cos+Sribik sin+ n (Дк-Вк)sin-Ak n cos-

i=1 i=1

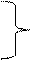Ak/kw*m sin-(Dk-Bk)/kw*cos m

*

Pk= SCiAik-n(Дк-Вк)-Ак/kw*m

Для решения системы необходимо определить вектор

[x]=[Аik,Bik,Pk,Tk]т=[A1k,A2k,Ank,B1k,...,Bnk,Pk,Tk]

Преобразуем систему (**) к следующей форме

.

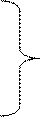-а11х1+х1=а12х2+а13х3+bV

.

-а21х1=а22х2+а23х3+b3V-х2

.

а31х1=а32х2+а33х3+b3V-x3

..

-A1x1+C1x1=A2x1+BV+C2x1

В качестве х1 может выступать любая фазовая координата, входящая в выход системы

а11 1 а12 а13

А1= а21 С1= 0 А2= а22 а23

а31 0 а32 а33

[x1]т=[x2x3]

х1=Y/g1-g2*x2/g1-g3x3/g1=Y/g1-C3тх1

q2 q3

С3Т=

q1 qn

a1 a1b1 a1b2

a2 [b1,b2]= a2b1 a2b2

a3 a3b1 a3b2

..

-1/g1*A1*Y+1/q*C1*Y=[A2-A1C3т]x1+(C1C3т-С2)х1+BV (*)

Если в уравнении (*) все фазовые координаты и управляющее воздействие V и выход системы Y подставить в тригонометрической форме, т. е. в виде гармоник, то мы получим, следующую систему, и сравнивая полиномы в одинаковых функциях времени мы получим следующую систему.

-1/q1*[A1]Ak+kw/q1*[C1]Bk=[A2-A1C3т][Аik]+[C1C3т-

С2]*kw[Bpk]+[B]Pk

-1/g1*[A1]Bk-kw/q1*[C1]Ak=[A2-A1C3т][Bjk]-kw[C1C3т-

C2][Ajk]+[B]Tk

В результате решения данной системы мы получим:

[x] = [А2к,А3к,В2к,В3к,Рк,Тк]

Определяем для каждой гармоники 1, 3, 5,...

После нахождения [х] находим вектор астатизма, равный коэффициентам закона V.

Решая данную систему при различной структуре матрицы L, может быть найдено многообразие законов управления, при этом в качестве доопределения выступают точность заданной характеристики, то есть число гармоник, учавствующих в синтезе, а в качестве условия решаемости является условие устойчивости синтеза системы.

Пример:

W(p)= ¾¾¾¾¾¾¾¾¾

(a0p3+a1p3+a1p2+a2p)

объект с ПФ х=Ах+BV

ЭФ постоянного тока с независимым возбуждением (астатизм 1 порядка).

х=Ах+ВV

0 1 0 экономическая

A= 0 0 1 форма Лурье

0 -a2/a0 -a1/a0

В= 0 Qт=[100] - угол

1/a0

[x]т=[x1,x2,x3]

A1=[000] C3т=[00]

х1=[х2,х3]

1 0

А2= 0 1

-а2/a0 -a1/a0

Система алгебрарических уравнений для нахождения вектора х будет неизвестна

A2k

B2k

A3k

B3k

Pk

Tk

1/кw 0 0 0 0 0 A2k Bk

0 -kw1 0 0 0 0 B2k 0

-a2/a0 0 -a1/a0 -kw 1/a0 0 A3k = 0

0 -1/kw 0 0 0 0 B3k Ak

kw 0 0 1 0 0 Pk 0

0 -a2/a0 kw -a1/a0 0 1/a0 Tk 0

Решая матрицу n-раз получим n-гармоник всех фазовых координат (нужны 1 и 3 гармоники – решаем 2 раза).

V=CHX+ne+mòe0dt

[x]=[C1C2 n m]

V=Pk cos + Tk sin

Pk = C1A2k+C2A3k+n(-A1k)-(Дк-А1к)/(кu)

e=(Дк-А1к) sin – B1 cos

Tk=C1*B2k+C2B3k+n(Дк-Ак)-В1к

А21 А31 -А11 (-D1-A11)/w C1 P1

B21 B31 D1-A11 -B11/w C2 T1

=

A23 A33 -A13 (-D3-A13)/3w n P3

B23 B33 D3-A13 -B13/3w m T3

Решая систему алгебрарических уравнений (*) находим вектор оптимизированных коэффициентов х. После нахождения вектора х система должна быть проверена на устойчивость. Неустойчивость показывает на невозможность реализации заданного процесса при заданной структуре.

§. Постановка задачи оптимизации.

.

х=Ах+ВV

V=Cux+n(1-Y)+mò(1-Y)dt

Y=Qx

Н-матрицы измерителя; фаз чисел: в нахождении фаз координат учавствуют в формировании залога управления.

В практическом смысле будем рассматривать следующую задачу: необходимо минимизировать структурные матрицы Н, т. е. найти то количество и те виды обратных связей, которые обеспечивают заданный выход Y, то есть заданное количество управления.

Данная задача называется задачей о минимизации полей регулирования и в настоящее время в общем виде не решена.

Решение данной задачи состоит из нескольких этапов.

Этапы решения задачи:

1) Задают выход системы Y исскуственно периодизируется и соответственно решение апроксимируется тригонометрическим рядом Фурье.

Y=Qx, получим Ak и Bk.

2) По заданным Ak и Bk находим гармоники фазовых координат и управляющего воздействия (смотри предыдущие лекции).

3) Подставляя найденные гармоники в уравнение (**) управляющего воздействия получим систему алгебраических уравнений.

4) Решая данную систему алгебраических уравнений для реализации структуры Н, находим соответствующий вектор x.

5) Проверяем систему на устойчивость. Если она устойчивая, то структура матрицы Н найдена, если система неустойчива, то надо уравнение (**) матрицы Н, проверить при других структурах.

То за счёт организации простейшей итеррациональной процедуры включающей в себя в себя решение системы алгебраических уравнений и анализ устойчивости может быть найден закон управления, содержащий найденные значения управления содержащие минимальное число фазовых координат.

Задача оптимизации по быстродействию.

Задана наша система; задана структура Н; форма переходного процесса на выходе.

Различную длительность переходного процесса мы учитываем за счёт w. w – корректирует длительность переходного процесса.

1) Задаём минимально возможное время переходного процесса, то есть максимальное w.

2) Находим все значения Ак и Вк.

3) Находим систему уравнений (**).

4) Находим вектор х для данной структуры Н.

5) Анализ устойчивости.

Если устойчива Þ произошла оптимизация системы.

Если нет Þ меням w.

Если при рабочем быстродействии получаем неучтойчивую систему, то делаем вывод о невозможности реализации заданной формы переходного процесса при заданной структуре матрицы Н.

§. Алгоритмическая процедура задачи

Летова-Калмана.

Нулевое начальное условие

x(f=0)=x0 (все параметры х=0)

В классическом понимании задача рассматривает движение системы из (×) х0 в начало координат.

Понятие о программном и стабилизирующем

управлении.

Система стабилизации.

b

хn x

объект

DV x+Dx

хэт

Под действием программного управления объект имеет выход х.

Однако под действием f выход=х+Dх. Сравниваем с эталоном на выходе DV воздействующим на объект и вызывающих движение по эталонной траектории (робот).

DV – стабилизирующее управление

xn – подпрограммное управление.

Данная задача решается на основе использования квадратичных оценок качества.

х

1 кривая 3 лучше 2

ty

х0 ò(х0-хт)dt

0

3 2

t

V2+(C1Dx+C2Dx+...+CnDxn)

¥

J=ò(xтQx+VтV)dt

При этом на нашу задачу накладывается ограничение; стабилизируется минимумы данной функции по n.

хт – транспонирует вектор – столбец фаз координат.

V – вектор управления.

V1 a

объект

Vn an

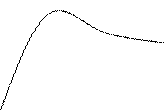
Если имеется объект, у него много выходов, но иногда угол уменьшает своё управляющее воздействие.

Мы с вами до сих пор рассматривали обречённые системы (один вход и выход). Х роботов, станков – многомерные системы.

Q – матрицы весовых коэффициентов.

j 1

Кривая 1 имеет меньше среднеквадратичных ошибок, чем 2, однако процесс 1 не работоспособен, а процесс 2 – работоспособен.

Качество управления в данном случае будет задаваться с помощью коэффициента матрицы Q. В общем случае проблема выбора коэффициентов матрицы Q не решена.

Y=Ax+BV x(0)=x0

¥

J=ò(xтQx+U1U)dt (+)

V=Cтx

PA+A1P-PBBтР+Q=0 (*)

r=-PB

Нужно выбрать такое Ст, чтобы уменьшать функционал (+).

Данная задача сводится к выражению (D), где Р - решение матричного уравнения (*).

(*) – матричное уравнение Рикикки.

Этапы решения задачи:

1. Выбираем матрицу q исходя из требований к переходному процессу.

Выбор q не поддаётся строгой формализации.

2. Сопоставляем уравнение Рикокки – это нелинейное алгебраическое уравнение, решение которого в общем виде нетривиальная задача.

Однако в силуособенностей уравнения P в настоящее время разработана стандартная h (программное его решение).

3. Находим матрицу С(D).

4. Находим закон управления.

Весь процесс формализирован и не поддаётся решению на ЭВМ.

5. Проверка качества системы (построение переходного процесса на кальке).

Если качество процесса не устраивает нас, то изменяем матрицу q и повторяем решения.

Выбор матрицы q-интуитивный процесс, зависит от квалификации работника.

Т. О. Процесс будучи интеррациональным постоянно приближен к заданному качеству системы.

Примечание: В настоящее время есть рекомендации по выбору q по корневым системам качества и по постоянным.

По корневым: Q выбираем из условия нахождения корней замкнутой системы по окружности радиуса.

По постоянным: с такими же параметрами.

R

Dj ³ 60° - запас по фазе.

DА ³ 2 дб - запас по амплитуде.

M £ 2 – колебательность.

Однако, этот материал находится на уровне журнальных статей.

Недостатки:

1) Выбор q.

2) Необходимо измерить и реализовать все фазовые координаты системы.

3) Закон управления получается в численной форме.

Если невозможно измерить все фазовые координаты, то нужно идентифицировать систему.

Пример:

..

х1 = х2

.

х2 = а22х2 + а23х3

.

х3 = а32х2 + а33х3 + b31V

V = C1x1 + C2x2 + C3x3

0 0 1 0 q11 0 0

[B] = 0; [A] = 0 a22 a23; Q = 0 q22 0

b31 0 a32 a33 0 0 q33

P11 P12 P13 0 1 0 0 0 0

P21 P22 P23 0 a22 a23 + 1 a22 a23 x

P31 P32 P33 0 a32 a33 0 a32 a33

P11 P12 P13 P13 b31

P21 P22 P23 - P23 b31 × [p13b31; p23b31; p33b31] +

P31 P32 P33 P33 b31