
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение нелинейных уравнений с помощью средства MS Excel Подбор параметра
|
|
Задание 1.
Постановка задачи. Дано уравнение: x3–0,01x2–0,7044x+0,139104 = 0. Необходимо решить его с помощью средства MS Excel Подбор параметра с точностью 0,001 [6].
Выполнение. Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x) = 0является точка пересечения графика функции f(x) с осью абсцисс, т. е. такое значение x, при котором функция обращается в ноль.
Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0,2. Результаты вычислений приведены на рис.1, где в ячейку В2 была введена формула: = A2^3-0,01*A2^2-0,7044*A2+0,139104.
На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеет не более трех вещественных корней, то графическое решение поставленной задачи найдено: была проведена локализация корней, т. е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].
Теперь можно найти корни полинома методом последовательных приближений с помощью команды: Сервис → Подбор параметра. Относительная погрешность вычислений и предельное число итераций (например, 0,00001 и 1000) задаются на вкладке Сервис → Параметры.

Рис.1. Результаты вычислений
В поле Установить в ячейке дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения (уравнение должно быть записано таким образом, чтобы его правая часть не содержала переменную). В поле Значение вводим правую часть уравнения, а в поле Изменяя значения ячейки дается ссылка на ячейку, отведенную под переменную. Заметим, что вводить ссылки на ячейки в поля диалогового окна Подбор параметров удобнее не с клавиатуры, а щелчком на соответствующей ячейке.
 Рис.2. Диалоговое окно «Подбор параметра»
Рис.2. Диалоговое окно «Подбор параметра»
|
После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра (рис. 3.) с сообщением об успешном завершении поиска решения приближенное значение корня будет помещено в ячейку А14.

Рис. 3. Диалоговое окно «Результат подбора параметра»
 Рис.4. Результаты вычислений
Рис.4. Результаты вычислений
|
Задание 2.
Постановка задачи. Дано уравнение: ex – (2x – 1)2 = 0.
Необходимо решить его с помощью средства MS Excel Подбор параметра – с точностью 0,001.
Выполнение. Проведем локализацию корней нелинейного уравнения.
Для этого представим его в виде f(x) = g(x),
т. е. ex = (2x -1)2 или f(x) = e x, g(x) = (2x – 1) 2 и решим графически.
Графическим решением уравнения
f(x) = g(x)
будет точка пересечения линий f(x) и g(x).
Построим графики f(x) и g(x). Для этого в диапазон А3:А18 введем значения аргумента. В ячейку В3 введем формулу для вычисления значений функции:
f(x) = EXP(A3),
а в ячейку С3 –
g(x) = (2*A3-1)^2.
Результаты вычислений и построение графиков f(x) и g(x) в одной графической области показаны на рис.5.

Рис. 5. Результаты вычислений и построение графиков f(x) и g(x )
На графике видно, что линии f(x) и g(x) пересекаются дважды, т. е. данное уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно:

Для второго можно определить интервал изоляции корня: 1,5 < x < 2.
Теперь можно найти корень уравнения на отрезке [1.5,2] методом последовательных приближений.
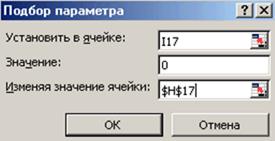 Рис.6. Диалоговое окно «Подбор параметра»
Рис.6. Диалоговое окно «Подбор параметра»
|
Введём начальное приближение в ячейку Н17 = 1,5 и само уравнение (со ссылкой на начальное приближение) в ячейку I17 = EXP(H17) – (2*H17–1) ^2 (рис. 5).
Далее воспользуемся пунктом меню Сервис → Подбор параметра и заполним диалоговое окно Подбор параметра (рис.6).
Результат поиска решения будет выведен в ячейку Н17 (рис.).

Рис.7. Результат поиска решения
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Можно ли произвольно задавать значения на отрезке по оси х для определения корней?
2. Что при определении корней называют критическими точками?
3. Сколько корней может быть у функции, если у нее существует лишь одна критическая точка?
4. Какие основные проблемы могут встретиться при аналитическом определении корней?
| <== предыдущая | | | следующая ==> |
| Право в системе социальных норм | | | Грамматическая основа предложения |
Date: 2016-05-14; view: 3270; Нарушение авторских прав