
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод опорных векторов
|
|
В настоящее время одним из лучших методов классификации считается метод опорных векторов SVM (support vector machine, машины опорных векторов), который обладает несколькими замечательными свойствами:
1) обучение сводится к задаче квадратичного программирования, имеющей единственное решение, которое вычисляется достаточно эффективно даже на выборках в сотни тысяч объектов;
2) решение обладает свойством разреженности, т.е. положение оптимальной разделяющей гиперплоскости зависит лишь от небольшой доли обучающих объектов, которые и называются опорными векторами, а остальные объекты фактически не задействуются;
3) с помощью введения функции ядра метод обобщается на случай нелинейных разделяющих поверхностей.
Пусть имеется множество обучающих примеров {(Xi, Yi), i = 1, …, L }, где Xi – n -мерный вектор признаков i -го объекта обучающей выборки, Yi – метка класса i -го объекта, Yi Î {–1, +1}. В случае случая линейно разделимых классов уравнение разделяющей гиперплоскости записывается следующим образом:
WTX + b = 0,
где W – вектор весов, b – пороговое значение, что определяет решающее правило классификации:

Для данного вектора весов и порогового значения расстояние между гиперплоскостью и ближайшей точкой из набора данных называется границей разделения. Основной задачей, решаемой методом опорных векторов, является поиск конкретной гиперплоскости, для которой граница разделения будет максимальной. При этом условии поверхность решения называется оптимальной гиперплоскостью.
Пусть Wo и bo – оптимальные значения вектора весов и порога соответственно. Исходя из этого, оптимальную гиперплоскость, представляющую многомерную линейную поверхность решений в пространстве признаков, можно описать уравнением:
 .
.
При этом разделяющая функция имеет вид:
 .
.
Она определяет алгебраическую меру расстояния от точки X до оптимальной гиперплоскости.
Точку X в признаковом пространстве можно выразить следующим образом:
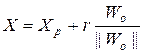 ,
,
где Xp – нормальная проекция точки X на оптимальную гиперплоскость, r – расстояние от точки до оптимальной гиперплоскости (величина r положительна либо отрицательна в зависимости от того с какой стороны от нее находится точка X). С учетом указанного выше получаем:

или
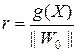 .
.
Точки, ближайшие к разделяющей гиперплоскости, являются опорными векторами. Геометрический зазор – это максимальная ширина полосы, которую можно провести между опорными векторами двух классов, т.е. это значение, превышающее в два раза минимальное значение r. Поскольку масштабирование параметров Wo и bo не меняет величину геометрического зазора, то можно ввести следующее условие:

Таким образом, для всех точек должно выполняться неравенство
 ,
,
и должны существовать опорные векторы, для которых оно превращается в равенство. Поскольку расстояние ri от точки Xi до гиперплоскости равно
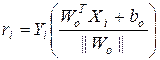 ,
,
то геометрический зазор равен
 .
.
Таким образом, требуется найти значения параметров W и b, удовлетворяющие следующим условиям:
1) достигается максимум величины геометрического зазора  ,
,
2) при всех (Xi, Yi) из множества обучающих примеров справедливо:
 .
.
Задача максимизации величины  эквивалентна задаче минимизации величины
эквивалентна задаче минимизации величины  и, следовательно, задаче минимизации величины
и, следовательно, задаче минимизации величины  . Это приводит к следующей формулировке задачи оптимизации в методе опорных векторов:
. Это приводит к следующей формулировке задачи оптимизации в методе опорных векторов:
найти значения параметров W и b, удовлетворяющие следующим условиям:
1) величина  достигает минимума,
достигает минимума,
2) при всех (Xi, Yi) из множества обучающих примеров справедливо:
 .
.
Данная формулировка соответствует задаче квадратичной оптимизации. Для того, чтобы найти ее решение, необходимо сформулировать двойственную задачу, в которой с каждым линейным ограничением  прямой задачи связан соответствующий множитель Лагранжа ai. В такой формулировке требуется найти a 1, a2, …, aL, при которых
прямой задачи связан соответствующий множитель Лагранжа ai. В такой формулировке требуется найти a 1, a2, …, aL, при которых
1) величина  достигает максимума,
достигает максимума,
2) 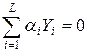 ,
,
3) ai ³ 0 при всех i = 1, 2, …, L.
Решение указанной задачи имеет следующий вид:

В этом решении большинство параметров ai равно нулю. Каждое ненулевое значение ai означает, что соответствующий вектор Xi является опорным. Таким образом, функция классификации имеет следующий вид:
 .
.
Для решения двойственной задачи можно воспользоваться алгоритмом Джона Платта:
1. Начать с набора { ai, i = 1, …, L }, удовлетворяющего ограничениям;
2. Выбрать пару (ai, aj);
3. При фиксированных значениях остальных множителей и имеющихся ограничениях  и ai, aj ³ 0 выбрать оптимальную пару значений (мини-оптимизация);
и ai, aj ³ 0 выбрать оптимальную пару значений (мини-оптимизация);
4. Продолжать процесс до наступления условий завершения.
В случае, когда классы не являются линейно разделимыми, выполняется отображение классифицируемых точек в пространство более высокой размерности:
F: X ® f (X).
Это равносильно переходу от скалярного произведения  к ядру K (Xi, X):
к ядру K (Xi, X):
 .
.
Ядро K должно быть непрерывным, симметричным, а также иметь положительно определенную матрицу Грама. Эти условия гарантируют, что существуют отображение в воспроизводящее ядро гильбертова пространства (гильбертово пространство – векторное пространство, полное относительно скалярного произведения), т.е. пространство, скалярное произведение в котором совпадает со значением функции K. Наиболее распространенными семействами ядер являются:
- полиномиальные ядра:
 ,
,
- функции радиального базиса:

Стандартный метод опорных векторов предназначен для бинарной классификации. Для случая нескольких классов наиболее часто применяются следующие два подхода:
1. Создается набор классификаторов, работающих по принципу «один против остальных» или «один против всех», а затем выбирается класс, на котором объект отстоит дальше всего от разделяющей поверхности;
2. Создается набор бинарных классификаторов, а затем выбирается класс, предложенный большинством классификаторов.
Задание
1. Подготовить обучающую выборку не менее чем из 8 объектов, разделенных на 2 класса. В качестве признаков и их значений использовать:
1) возраст – пожилой, средний, молодой;
2) пол – мужской, женский;
3) стадия болезни – поздняя, начальная, средняя;
4) больное место – голова, спина, живот, руки, ноги, отсутствует;
5) температура – пониженная (ниже 36.6°), нормальная (36.6°), незначительно повышенная (выше 36.6° и не ниже 38°), значительно повышенная (свыше 38°);
6) прочие ощущения – озноб, отсутствие аппетита, тошнота, отсутствуют.
Пример обучающей выборки приведен в таблице 1.
2. Написать программы классификации объектов с помощью линейных решающих функций и метода опорных векторов.
3. Подготовить тестовую выборку и проверить на ней работу алгоритмов классификации.
Таблица 1. Обучающая выборка
| № | Класс | Возраст | Пол | Стадия болезни | Больное место | Температура | Прочие ощущения |
| w1 | Пожилой | Мужской | Поздняя | Голова | Нормальная | Отсутствие аппетита | |
| w1 | Пожилой | Мужской | Поздняя | Спина | Нормальная | Тошнота | |
| w1 | Пожилой | Мужской | Средняя | Спина | Незначительно повышенная | Тошнота | |
| w1 | Средний | Женский | Начальная | Отсутствует | Пониженная | Отсутствуют | |
| w2 | Молодой | Женский | Начальная | Руки | Незначительно повышенная | Озноб | |
| w2 | Средний | Женский | Начальная | Живот | Нормальная | Озноб | |
| w2 | Молодой | Женский | Начальная | Ноги | Значительно повышенная | Озноб | |
| w2 | Молодой | Мужской | Средняя | Отсутствует | Нормальная | Отсутствуют |
Date: 2016-05-13; view: 964; Нарушение авторских прав