
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические рекомендации к выполнению ТР
|
|
И методические рекомендации к ней
Для студентов очной формы обучения для инженерных направлений
Учебно-методическое пособие
ТР Дифференциальные уравнения
Часть 1. Дифференциальные уравнения первого порядка и второго порядка, допускающие понижение порядка
Теоретические вопросы:
1. Основные понятия теории дифференциальных уравнений. Задача Коши для дифференциального уравнения первого порядка.
2. Дифференциальные уравнения первого порядка: с разделяющимися переменными, однородные и приводящиеся к однородным.
3. Линейные уравнения первого порядка, уравнения Бернулли.
4. Дифференциальные уравнения  - ого порядка, допускающие понижение порядка.
- ого порядка, допускающие понижение порядка.
5. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
Расчетные задания
Задание 1. Найти общее решение дифференциальных уравнений.
1.1 1)  ; 2)
; 2)  ;
;
3)  .
.
1.2 1)  ; 2)
; 2)  ;
;
3)  .
.
1.3 1)  ; 2)
; 2)  ;
;
3) 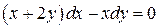 .
.
1.4 1)  ; 2)
; 2)  ;
;
3)  .
.
1.5 1)  ; 2)
; 2)  ;
;
3)  .
.
1.6 1)  ; 2)
; 2)  ;
;
3)  .
.
1.7 1)  ; 2)
; 2)  ;
;
3)  .
.
1.8 1)  ; 2)
; 2)  ;
;
3)  .
.
1.9 1)  ; 2)
; 2)  ;
;
3)  .
.
1.10 1)  ; 2)
; 2)  ;
;
3) 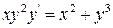 .
.
1.11 1)  ; 2)
; 2)  ;
;
3)  .
.
1.12 1)  ; 2)
; 2)  ;
;
3)  .
.
1.13 1)  ; 2)
; 2)  ;
;
3)  .
.
1.14 1)  ; 2)
; 2)  ;
;
3)  .
.
1.15 1)  ; 2)
; 2)  ;
;
3)  .
.
1.16 1)  ; 2)
; 2)  ;
;
3)  .
.
1.17 1)  ;
;
2)  ;
;
3)  .
.
1.18 1)  ; 2)
; 2)  ;
;
3)  .
.
1.19 1)  ; 2)
; 2)  ;
;
3)  .
.
1.20 1)  ; 2)
; 2)  ;
;
3)  .
.
1.21 1)  ; 2)
; 2)  ;
;
3)  .
.
1.22 1)  ;
;
2)  ;
;
3)  .
.
1.23 1)  ; 2)
; 2)  ;
;
3)  .
.
1.24 1)  ; 2)
; 2)  ;
;
3)  .
.
1.25 1)  ;
;
2)  ;
;
3) 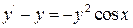 .
.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющего начальному условию.
2.1,.
2.2,.
2.3,.
2.4,.
2.5,.
2.6.,.
2.7.,.
2.8,.
2.9,.
2.10,.
2.11,.
2.12,.
2.13,.
2.14,.
2.15,.
2.16,.
2.17,.
2.18,.
2.19,.
2.20,.
2.21,.
2.22,.
2.23,.
2.24,.
2.25,.
Задание 3. Найти частное решение дифференциального уравнения и вычислить полученное значение функции при  с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой.
3.1  ,
,  ,
,  ,
,  ,
,  .
.
3.2  ,
,  ,
,  ,
,  .
.
3.3  ,
,  ,
,  ,
,  .
.
3.4  ,
,  ,
,  ,
,  ,
,  .
.
3.5  ,
,  ,
,  ,
,  .
.
3.6  ,
,  ,
,  ,
,  .
.
3.7  ,
,  ,
,  ,
,  .
.
3.8  ,
,  ,
, 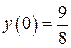 ,
,  ,
,  .
.
3.9  ,
,  ,
,  ,
,  .
.
3.10  ,
,  ,
,  ,
,  .
.
3.11  ,
,  ,
,  .
.
3.12  ,
,  ,
,  ,
,  .
.
3.13  ,
,  ,
,  ,
,  ,
,  .
.
3.14  ,
,  ,
,  ,
,  .
.
3.15  ,
,  ,
, 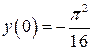 ,
,  .
.
3.16  ,
,  ,
,  .
.
3.1 7  ,
,  ,
,  ,
,  ,
,  .
.
3.18  ,
,  ,
,  ,
,  ,
, 
3.19  ,
,  ,
,  ,
,  .
.
3.20  ,
,  ,
, 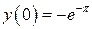 ,
,  .
.
3.21  ,
,  ,
,  ,
,  .
.
3.22  ,
,  .
.  ,
,  .
.
3.23  ,
,  ,
,  ,
,  .
.
3.24  ,
,  ,
,  ,
,  .
.
3.25  ,
,  ,
,  ,
,  .
.
Задание 4. Найти решение дифференциального уравнения, допускающего понижение порядка.
4.1 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.2 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.3 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.4 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.5 1)  , 2)
, 2)  ,
, 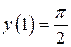 ,
,  .
.
4.6 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.7 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.8 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.9 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.10 1) 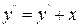 , 2)
, 2)  ,
,  ,
,  .
.
4.11 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.12 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.13 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.14 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.15 1)  ,
,  ,
,  , 2)
, 2)  .
.
4.16 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.17 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.18 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.19 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.20 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.21 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.22 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.23 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.24 1)  , 2)
, 2)  ,
,  ,
,  .
.
4.25 1)  , 2)
, 2)  ,
,  ,
,  .
.
Часть 2. Дифференциальные уравнения с постоянными коэффициентами
Теоретические вопросы:
1. Линейно-зависимые и линейно-независимые системы функций. Необходимое условие линейной зависимости системы функций.
2. Условие линейной независимости решений линейного однородного дифференциального уравнения.
3. Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Фундаментальная система решений. Структура общего решения.
4. Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. Структура общего решения.
5. Метод Лагранжа вариации произвольных постоянных.
6. Линейная система дифференциальных уравнений с постоянными коэффициентами (метод характеристического уравнения, метод исключения).
Расчетные задания
Задание 1. Найти общее решение дифференциальных уравнений.
1.1 1) 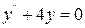 ; 2)
; 2)  ;
;
3)  .
.
1.2 1)  ; 2)
; 2)  ;
;
3)  .
.
1.3 1) 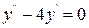 ; 2)
; 2)  ;
;
3)  .
.
1.4 1)  ; 2)
; 2)  ;
;
3)  .
.
1.5 1)  , 2)
, 2)  ;
;
3)  .
.
1.6 1) 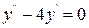 ; 2)
; 2)  ;
;
3)  .
.
1.7 1)  , 2)
, 2)  ;
;
3)  .
.
1.8 1) 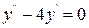 ; 2)
; 2)  ;
;
3)  .
.
1.9 1)  ; 2)
; 2)  ;
;
3)  .
.
1.10 1)  ; 2)
; 2)  ;
;
3)  .
.
1.11 1)  ; 2)
; 2)  ;
;
3)  .
.
1.12 1)  ; 2)
; 2)  ;
;
3)  .
.
1.13 1)  ; 2)
; 2)  ;
;
3)  .
.
1.14 1)  ; 2)
; 2)  ;
;
3)  .
.
1.15 1)  ; 2)
; 2)  .
.
3)  .
.
1.16 1)  ; 2)
; 2)  ;
;
3)  .
.
1.17 1)  ; 2)
; 2)  ;
;
3)  .
.
1.18 1)  ; 2)
; 2)  ;
;
3)  .
.
1.19 1)  ; 2)
; 2)  ;
;
3)  .
.
1.20 1)  ; 2)
; 2)  ;
;
3)  .
.
1.21 1)  ; 2)
; 2)  ;
;
3)  .
.
1.22 1)  ; 2)
; 2)  ;
;
3) 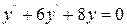 .
.
1.23 1)  ; 2)
; 2)  ;
;
3)  .
.
1.24 1)  ; 2)
; 2)  ;
;
3)  .
.
1.25 1) 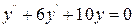 ; 2)
; 2)  ;
;
3)  .
.
Задание 2. Записать структуру частного решения линейного неоднородного уравнения по виду правой части.
2.1 
а)  ; б)
; б)  .
.
2.2 
а)  ; б)
; б)  .
.
2.3 
а)  ; б)
; б)  .
.
2.4 
а)  ; б)
; б)  .
.
2.5 
а)  ; б)
; б)  .
.
2.6 
а)  ; б)
; б)  .
.
2.7 
а)  ; б)
; б)  .
.
2.8 
а)  ; б)
; б)  .
.
2.9 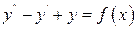
а)  ; б)
; б)  .
.
2.10 
а)  ; б)
; б)  .
.
2.11 
а)  ; б)
; б)  .
.
2.12 
а)  ; б)
; б)  .
.
2.13 
а)  ; б)
; б)  .
.
2.14 
а)  ; б)
; б) 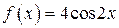 .
.
2.15 
а)  ; б)
; б)  .
.
2.16 
а)  ; б)
; б)  .
.
2.17 
а)  ; б)
; б)  .
.
2.18 
а)  ; б)
; б)  .
.
2.19 
а)  ; б)
; б)  .
.
2.20 
а)  ; б)
; б)  .
.
2.21 
а)  ; б)
; б)  .
.
2.22 
а)  ; б)
; б)  .
.
2.23 
а)  ; б)
; б)  .
.
2.24 
а)  ; б)
; б)  .
.
2.25 
а)  ; б)
; б)  .
.
Задание 3. Найти общее решение дифференциальных уравнений.
3.1 1)  , 2)
, 2)  .
.
3.2 1)  ; 2)
; 2)  .
.
3.3 1)  ; 2)
; 2)  .
.
3.4 1)  ; 2)
; 2)  .
.
3.5 1)  ; 2)
; 2)  .
.
3.6 1)  ; 2)
; 2)  .
.
3.7 1)  , 2)
, 2)  .
.
3.8 1)  ; 2)
; 2)  .
.
3.9 1)  ; 2)
; 2)  .
.
3.10 1)  ; 2)
; 2)  .
.
3.11 1)  , 2)
, 2)  .
.
3.12 1)  ; 2)
; 2)  .
.
3.13 1)  ; 2)
; 2)  .
.
3.14 1)  ; 2)
; 2)  .
.
3.15 1)  ; 2)
; 2)  .
.
3.16 1)  ; 2)
; 2)  .
.
3.17 1) 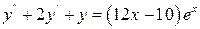 ; 2)
; 2)  .
.
3.18 1)  ; 2)
; 2)  .
.
3.19 1)  ; 2)
; 2)  .
.
3.20 1)  ; 2)
; 2)  .
.
3.21 1)  ; 2)
; 2)  .
.
3.22 1)  ; 2)
; 2)  .
.
3.23 1)  ; 2)
; 2) 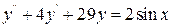 .
.
3.24 1)  ; 2)
; 2)  .
.
3.25 1)  ; 2)
; 2)  .
.
Задание 4. Решить дифференциальное уравнение методом вариации произвольных постоянных.
4.1  4.2
4.2 
4.3  ; 4.4
; 4.4 
4.5  ; 4.6
; 4.6 
4.7  4.8
4.8 
4.9  4.10
4.10 
4.11  4.12
4.12 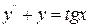
4.13  4.14
4.14 
4.15  4.16
4.16 
4.17  4.18
4.18 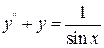
4.19  4.20
4.20 
4.21  4.22
4.22 
4.23  4.24
4.24 
4.25 
Задание 5. Решить систему дифференциальных уравнений двумя способами: 1) сведением к дифференциальному уравнению; 2) с помощью характеристического уравнения.
5.1  5.2
5.2 
5.3  5.4
5.4 
5.5 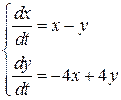 5.6
5.6 
5.7  5.8
5.8 
5.9  5.10
5.10 
5.11  5.12
5.12 
5.13  5.14
5.14 
5.15  5.16
5.16 
5.17  5.18
5.18 
5.19  5.20
5.20 
5.21  5.22
5.22 
5.23  5.24
5.24 
5.25 
Методические рекомендации к выполнению ТР
Основные теоретические сведения
1. Уравнение вида  называется дифференциальным уравнением с разделяющимися переменными. Его общим интегралом будет
называется дифференциальным уравнением с разделяющимися переменными. Его общим интегралом будет
 .
.
2. Дифференциальное уравнение  называется однородным относительно переменных
называется однородным относительно переменных  и
и  , если
, если  - однородная функция нулевого измерения относительно своих аргументов, т.е.
- однородная функция нулевого измерения относительно своих аргументов, т.е.  . Данное уравнение с помощью замены
. Данное уравнение с помощью замены  сводится к уравнению с разделяющимися переменными.
сводится к уравнению с разделяющимися переменными.
3. Уравнение 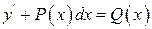 называется линейным дифференциальным уравнением. Общее решение уравнения находим по формуле
называется линейным дифференциальным уравнением. Общее решение уравнения находим по формуле
 .
.
4. Уравнение вида
 ,
,
где  и
и  - постоянные числа называется линейным однородным дифференциальным уравнением второго порядка. Квадратное уравнение
- постоянные числа называется линейным однородным дифференциальным уравнением второго порядка. Квадратное уравнение  называется характеристическим уравнением.
называется характеристическим уравнением.
Если корни  характеристического уравнения действительны и различны, то общий интеграл уравнения
характеристического уравнения действительны и различны, то общий интеграл уравнения  выражается формулой
выражается формулой
 .
.
Если  , то общий интеграл уравнения
, то общий интеграл уравнения  находится по формуле
находится по формуле
 .
.
Если  , то общее решение уравнения
, то общее решение уравнения  находится по формуле
находится по формуле
 .
.
5. Уравнение вида

называется неоднородным линейным уравнением второго порядка. Если  - общее решение соответствующего однородного уравнения,
- общее решение соответствующего однородного уравнения,  - частное решение уравнения
- частное решение уравнения  , то общее решение уравнения
, то общее решение уравнения  имеет вид
имеет вид  .
.
Укажем правило нахождения частного решения  уравнения
уравнения  методом неопределенных коэффициентов.
методом неопределенных коэффициентов.
Пусть  , тогда
, тогда
1)  , если
, если  не является корнем характеристического уравнения;
не является корнем характеристического уравнения;
2)  , если
, если  является простым корнем характеристического уравнения;
является простым корнем характеристического уравнения;
3)  , если
, если  двукратным корнем характеристического уравнения.
двукратным корнем характеристического уравнения.
Пусть  , тогда:
, тогда:
1)  , если число
, если число  является корнем характеристического уравнения;
является корнем характеристического уравнения;
2)  , если число
, если число  не является корнем характеристического уравнения.
не является корнем характеристического уравнения.
Пример 1. Найти общее решениеуравнения
 - НДУ
- НДУ
 - структура общего решения НДУ.
- структура общего решения НДУ.
Характеристическое уравнение  имеет корни
имеет корни  ,
,  .
.
 - общее решение ОДУ.
- общее решение ОДУ.
По функции  запишем структуру частного решения
запишем структуру частного решения  .
.
 .
.

Найденные выражения  ,
, 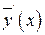 ,
,  подставляем в исходное уравнение и, разделив обе его части на
подставляем в исходное уравнение и, разделив обе его части на  , получаем уравнение
, получаем уравнение
 .
.
Приравнивая коэффициенты при  ,
,  ,
,  , получаем систему, решая ее находим
, получаем систему, решая ее находим  и
и  .
.
 .
.
 ,
,  .
.
 - частное решение НДУ.
- частное решение НДУ.
 - общее решение ОДУ.
- общее решение ОДУ.
Пример 2. Найти решение дифференциальных уравнений методом характеристического уравнения.



Решение. Частное решение системы будем находить в следующем виде  ,
, 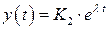 . Требуется определить постоянные
. Требуется определить постоянные  и
и 
 удовлетворяли заданной системе уравнений. Подставляя их в систему и сокращая на
удовлетворяли заданной системе уравнений. Подставляя их в систему и сокращая на  , получим систему уравнений:
, получим систему уравнений:

Составляем характеристическое уравнение и решаем его:


 - корни характе
- корни характе
Date: 2016-05-14; view: 329; Нарушение авторских прав