
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения типовых задач
|
|
Задача № 1
Для изготовления двух видов продукции  и
и  используются четыре вида ресурсов
используются четыре вида ресурсов  ,
, 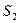 ,
, 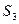 и
и 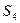 . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1.1.
. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице 1.1.
Таблица 1.1
| Вид ресурса | Запас ресурса | Число единиц ресурсов, затрачиваемых на изготовление единицы продукции | |

| 
| ||
| S1 | |||
| S2 | |||
| S3 | - | ||
| S4 | - |
Прибыль, получаемая от единицы продукции  и
и  – соответственно 4 и 5 руб.
– соответственно 4 и 5 руб.
Необходимо составить такой план производства продукции, чтобы прибыль от ее реализации была максимальной.
Составим экономико-математическую модель данной задачи. Введем обозначения:  и
и 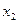 – число единиц продукции соответственно
– число единиц продукции соответственно  и
и  , запланированных к производству. Для их изготовления ресурса
, запланированных к производству. Для их изготовления ресурса  потребуется:
потребуется:
 (1)
(1)
Ресурса 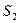 :
:
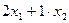 (2)
(2)
Ресурса 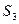 :
:
 (3)
(3)
И, наконец, 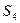 :
:
 (4)
(4)
Поскольку потребление ресурсов не должно превышать  ,
, 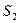 ,
, 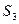 и
и 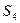 не должно превышать их запасов, соответственно 18, 16, 5 и 21 ед., то связь между потреблением ресурсов и их запасами выразится системой неравенств:
не должно превышать их запасов, соответственно 18, 16, 5 и 21 ед., то связь между потреблением ресурсов и их запасами выразится системой неравенств:
 (5)
(5)
Согласно условию задачи:
 (6)
(6)
Суммарная прибыль  от реализации двух видов продукции составит:
от реализации двух видов продукции составит:
 (7)
(7)
Таким образом, экономико-математическая задача: найти такой план выпуска продукции 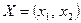 , удовлетворяющий системе (5) и условию (6), при котором функция (7) принимает максимальное значение.
, удовлетворяющий системе (5) и условию (6), при котором функция (7) принимает максимальное значение.
Строим область допустимых решений задачи. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (рис. 1) строим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств.
 (8)
(8)
Построив полученные прямые, найдём соответствующие полуплоскости допустимых значений переменных и их пересечение (рис. 1). Многоугольником допустимых решений задачи является шестиугольник 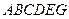 , координаты точек которого удовлетворяют условию неотрицательности переменных и неравенствам системы ограничений задачи.
, координаты точек которого удовлетворяют условию неотрицательности переменных и неравенствам системы ограничений задачи.
Строим вектор 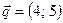 и одну из этих линий, например,
и одну из этих линий, например, 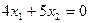 . Так как решается задача на отыскание максимума целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через точку
. Так как решается задача на отыскание максимума целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через точку  , определяемой системой уравнений:
, определяемой системой уравнений:
 (9)
(9)
В результате получим 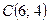 . Максимум линейной функции равен:
. Максимум линейной функции равен:
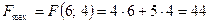
Геометрический метод прост и нагляден. Однако у него есть большой недостаток: данный метод применим только для задач с двумя неизвестными

Рис. 1.
Задача № 2
Построить первоначальный опорный план задачи, заданной матрицей планирования, методом северо-западного угла.
| поставщики | потребители | запасы | |||

| 
| 
| 
| ||

| |||||
| |||||

| |||||
| потребности | 1000=1000 |
Решение:
| поставщики | потребители | запасы | |||

| 
| 
| 
| ||

| 
| ||||
| 
| ||||

| 
| ||||
| потребности | 
| 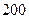
|  0 0
|  0 0
| 1000=1000 |
Последовательность заполнения клеток:
1.  . Первый столбец исключаем из дальнейшего рассмотрения (т.к. потребность в этом столбце стала равной 0 и это указываем рядом с исходным значением потребности), а запас первого поставщика уменьшается на 100 и становится равным 500.
. Первый столбец исключаем из дальнейшего рассмотрения (т.к. потребность в этом столбце стала равной 0 и это указываем рядом с исходным значением потребности), а запас первого поставщика уменьшается на 100 и становится равным 500.
2. В оставшейся таблице северо-западная клетка находится в первой строке и втором столбце  . Потребности второго потребителя полностью удовлетворены, второй столбец исключается из рассмотрения, а запас первого поставщика уменьшается на 200 единиц и становится равным 300 ед.
. Потребности второго потребителя полностью удовлетворены, второй столбец исключается из рассмотрения, а запас первого поставщика уменьшается на 200 единиц и становится равным 300 ед.
3.  . Запас первого поставщика исчерпан, первую строку исключаем из рассмотрения, а потребность третьего потребителя уменьшается на 300 единиц и становится равной 200 ед.
. Запас первого поставщика исчерпан, первую строку исключаем из рассмотрения, а потребность третьего потребителя уменьшается на 300 единиц и становится равной 200 ед.
4. 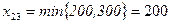 . Потребности третьего потребителя полностью удовлетворены, третий столбец исключается рассмотрения, а запас второго поставщика уменьшается на 200 единиц.
. Потребности третьего потребителя полностью удовлетворены, третий столбец исключается рассмотрения, а запас второго поставщика уменьшается на 200 единиц.
5. 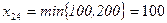 . Запас второго поставщика полностью исчерпан, вторую строку исключаем из рассмотрения, а потребность четвертого потребителя уменьшается на 100 единиц и становится равной 100 ед.
. Запас второго поставщика полностью исчерпан, вторую строку исключаем из рассмотрения, а потребность четвертого потребителя уменьшается на 100 единиц и становится равной 100 ед.
6. В таблице осталась одна строка и один столбец. Это последний шаг процесса,  .
.
Количество заполненных клеток равно 6,  . Следовательно, полученный план невырожденный
. Следовательно, полученный план невырожденный  . Значения базисных переменных
. Значения базисных переменных  ,
,  ,
,  ,
,  ,
,  ,
,  . Остальные переменные – свободные, их значения равны 0. Транспортные расходы (значение целевой функции):
. Остальные переменные – свободные, их значения равны 0. Транспортные расходы (значение целевой функции):
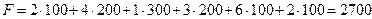 (единиц).
(единиц).
Задача № 3
Если условия транспортной задачи заданы в виде схемы, на которой условно изображены поставщики, потребители и связывающие их дороги, указаны величины запасов груза и потребности в нем, а также числа cij, являющиеся показателями принятого в задаче критерия оптимальности (тарифы, расстояния и т. п.), то говорят, что транспортная задача поставлена в сетевой форме (рис. 2).
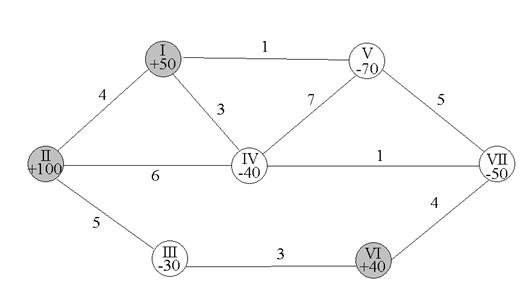
Рис. 2.
Пункты расположения поставщиков и потребителей будем изображать кружками и называть вершинами (узлами) сети, запасы груза будем записывать в кружках положительными, а потребности – отрицательными числами. Дороги, связывающие пункты расположения и потребления груза, будем изображать линиями и называть ребрами (дугами, звеньями) сети. На сети могут быть изображены вершины, в которых нет ни поставщиков, ни потребителей. Наличие таких вершин не повлияет на способ решения, если считать, что запасы (потребности) груза в них равны нулю.
Различия между транспортными задачами в матричной и сетевой формах весьма незначительны, так как методы их решения основаны на одних и тех же идеях (метод потенциалов). Решение задачи на сети начинается с построения начального опорного плана.
Последовательность решения задачи рассмотрим на конкретном примере (см. рис. 6.1). Поставку груза из вершины в вершину будем обозначать стрелками с указанием величины поставок.
Опорный план должен удовлетворять следующим требованиям:
1) все запасы должны быть распределены, а потребности удовлетворены;
2) к каждой вершине должна подходить или выходить из нее хотя бы одна стрелка;
3) общее количество стрелок должно быть на единицу меньше числа вершин  ;
;
4) стрелки не должны образовывать замкнутый контур.
План распределения груза, отвечающий этим требованиям, представлен на рис. 3.
Далее следует проверить план на оптимальность. Для этого вычисляем потенциалы. Одной из вершин (например, вершине 1) присвоим некоторое значение потенциала (например, равное 10).
Для наглядности потенциалы будем заключать в рамки. После этого, двигаясь по стрелкам, определяем потенциалы остальных вершин, руководствуясь правилом: если стрелка выходит из вершины, то к потенциалу этой вершины прибавляем показатель cij критерия оптимальности, если же направление стрелки противоположно, cij вычитаем (см. рис. 3).
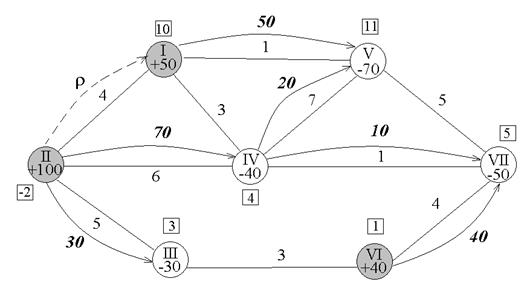
Рис. 3.
После вычисления потенциалов находят характеристики ребер без стрелок по правилу: из большего потенциала вычитается меньший, а разность вычитается из показателя cij, отвечающего данному ребру:
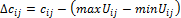
Если все ребра без стрелок имеют неотрицательные характеристики, то составленный план является оптимальным.
Вычислим характеристики ребер без стрелок:



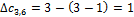
Три ребра имеют отрицательные характеристики, в этом случае выбирается ребро с наименьшей отрицательной характеристикой и к нему подрисовывается новая стрелка, при этом образуется замкнутый контур из стрелок. Новая стрелка направляется от вершины с меньшим потенциалом к вершине с большим потенциалом.
В нашем примере новая стрелка направлена от вершины II к вершине I (штриховая линия (см. рис. 3). Для определения величины поставки (ρ) для ребра  рассматриваются все стрелки образовавшегося замкнутого контура, имеющие направление, противоположное новой стрелке, и среди них находится стрелка с наименьшей поставкой λ (в нашем примере λ = 20 на ребре
рассматриваются все стрелки образовавшегося замкнутого контура, имеющие направление, противоположное новой стрелке, и среди них находится стрелка с наименьшей поставкой λ (в нашем примере λ = 20 на ребре  ). Выбранная таким образом величина прибавляется ко всем поставкам в стрелках, имеющих то же направление, что и новая стрелка, и вычитается из поставок в стрелках, имеющих противоположное направление. Поставки в стрелках, не входящих в контур, сохраняются неизменными. Стрелка, на которой выбрано число λ, ликвидируется, и общее число стрелок остается прежним. Новый опорный план представлен на рис. 4. Полученный план исследуется на оптимальность, подобно предыдущему.
). Выбранная таким образом величина прибавляется ко всем поставкам в стрелках, имеющих то же направление, что и новая стрелка, и вычитается из поставок в стрелках, имеющих противоположное направление. Поставки в стрелках, не входящих в контур, сохраняются неизменными. Стрелка, на которой выбрано число λ, ликвидируется, и общее число стрелок остается прежним. Новый опорный план представлен на рис. 4. Полученный план исследуется на оптимальность, подобно предыдущему.
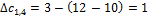



Определим оптимальное значение целевой функции:
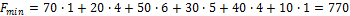
Вырождение плана транспортной задачи в сетевой постановке проявляется в том, что при полном использовании запасов и полном удовлетворении потребностей количество стрелок оказывается меньше чем  , где n – поставщики, а m – потребители. Для преодоления вырождения вводится нужное количество стрелок с нулевыми поставками, направление стрелок выбирается произвольно, однако они не должны образовывать замкнутый контур.
, где n – поставщики, а m – потребители. Для преодоления вырождения вводится нужное количество стрелок с нулевыми поставками, направление стрелок выбирается произвольно, однако они не должны образовывать замкнутый контур.

Рис. 4.
В случае открытой модели вводят фиктивного потребителя (поставщика) со спросом, равным небалансу. Фиктивный потребитель (поставщик) соединяется дугами непосредственно со всеми поставщиками (потребителями), при этом показатели cij ребер, соединяющих фиктивного потребителя (поставщика) с реальными поставщиками (потребителями), следует брать одинаковыми и сравнительно большими. Это делается для того, чтобы исключить возможность использования фиктивной вершины в качестве промежуточного пункта.
Задача № 4
Турист готовится к длительному переходу в горах. В рюкзаке он может нести груз, масса которого не более G кг. Груз может включать n предметов, причем i -й из них обладает массой q i кг, i = 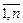 ; для каждого предмета турист определяет его ценность (полезность) с i во время перехода.
; для каждого предмета турист определяет его ценность (полезность) с i во время перехода.
Составить набор предметов таким образом, чтобы их суммарная масса не превосходила G, а суммарная полезность была наибольшей.
Обозначим х i = 0, если i -й предмет отвергается и х i = 1, если предмет берут в рюкзак.
Математическая модель задачи
 (3)
(3)
 (4)
(4)
 , где I =
, где I =  (5)
(5)
Метод ветвей и границ является одним из методов решения задачи о «рюкзаке».
Метод ветвей и границ (МВГ) относится к группе комбинаторных методов дискретного программирования и является одним из наиболее распространенных методов этой группы. В основу МВГ положены методы построения, позволяющие в ряде случаев существенно уменьшить объем перебора вариантов. МВГ – метод направленного перебора множества вариантов решения задачи. Графически перебор можно представить в виде дерева, т.е. связанного графа, но не содержащего циклов. Корень этого дерева все множество вариантов, а вершины дерева подмножества частично упорядоченных вариантов решения.
Идея метода состоит в том, что для ветвления выбираются те подмножества, которые имеют лучшую оценку. Трудность задачи в получении этой оценки.
Понятие оценки подмножества (множества)
· Если Мк – некоторое подмножество множества М, то оценкой множества Мк называется число (Мк) такое что,  для любого х
для любого х 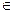 Мк, где f -целевая функция рассматриваемой оптимизационной задачи.
Мк, где f -целевая функция рассматриваемой оптимизационной задачи.
Алгоритм МВГ
1. Строятся вершины первого уровня. Для каждой вершины подсчитывается оценка φ (Мк). Ветвится вершина, которой соответствует максимальная оценка;
2. Для всех вершин j – го уровня (j = 2,3,…) подсчитывается оценка φ (Мк). Ветвится та из висячих вершин уровня j, у 2 – 1, …1, которой соответствует максимальная оценка.
3. Действия пункта 2 повторяются до тех пор пока не будет получено точное решение на последнем n -ом уровне. Конечная висячая вершина отвечает конкретному варианту х * = (х 1*, х 2*,…, х 4*). Для него подсчитывается точное значение целевой функции f (х *).
4. Если значение f (х *) не хуже оценок оставшихся вершин, т.е. f (х *) ≥ φ (Мк), то найдено оптимальное решение. Причем:
а) в случае строгого неравенства f (х *) > φ (Мк) оптимальное решение единственно.
б) для висячих вершин, в которых f (х *) = φ(Мк) производится ветвление и осуществляется поиск других оптимальных решений задачи в соответствии с пунктами 2 и 3.
Если значение f (х *) для вершин последнего уровня не лучше значения оставшихся висячих вершин, т.е. f (х *) < φ(Мк), то переходят на шаг 2.
При использовании алгоритма МВГ о задаче наилучшей загрузки «рюкзака» учитывают, что каждый предмет может быть выбран единственный раз в единичном количестве.
В общем случае имеется 2n вариантов, однако часть этих вариантов недопустима, т.к. соответствующий некоторому вектору х вариант может не удовлетворять ограниченного по максимальной загрузке «рюкзака», что позволяет дополнительно отсекать ветви.
Ветвление задачи организуется следующим образом:
1. Все множество вариантов М на два подмножества:
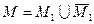 , где М1 – множество вариантов отвечающих х 1 = 1 (т.е. выбору первого предмета), а
, где М1 – множество вариантов отвечающих х 1 = 1 (т.е. выбору первого предмета), а  = М0 – множество вариантов, в которых первый предмет не выбирается (х 1 = 0).
= М0 – множество вариантов, в которых первый предмет не выбирается (х 1 = 0).
2. Дальнейшее ветвление ведется аналогично, т.е. разбиваем множества М0 и М1 по второй переменной х 2:
М1 = М11 U М10 и М01 U М00 и т.д.
В качестве оценки φ (Мj) каждого из рассматриваемых в задаче множеств Мj выбираем значение целевой функции f(х1*) соответствующее решениям также задачи (3) – (5), но без ограничения х i є {0,1} (т.е. допускается выбор кратных и нецелых частей предметов).
Решение этой вспомогательной задачи записывается в явном виде, если номера предметов упорядочены по удельным полезностям
 , т.е.
, т.е. 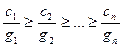 .
.
Оптимальное решение задачи (3) – (4) без учета условия (5) запишем, выбрав максимальное количество первых предметов:
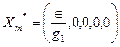 ;
; 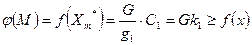 для
для 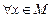 (*)
(*)
Указанное предварительное упорядочение заказов позволяет сформулировать эвристическое правило порядка ветвления правило порядка ветвления и для построения оценки каждого следующего множества Мj следует:
1. Смещаться по списку заказов на следующую позицию, добавляя к этой оценке уже имеющуюся часть f (х) отвечающую уже выбранным заказом.
2.Заменять 6 на оставшийся объем ресурса.
Задача 2
Пусть имеются все необходимые данные для задачи о «рюкзаке», которые уже упорядочены по убывающим Kj и G = 13 … (табл. 1).
Таблица 1
| I | |||||
| gi | |||||
| ci | |||||
| ki |
Решение:
1. Оценку множества М проводим в соответствии с соотношениями (*) берем относительное решение вспомогательной задачи х м*= ( , 0, 0, 0, 0) на котором получим оценку множества М:
, 0, 0, 0, 0) на котором получим оценку множества М:
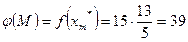
2. Произведем разбиение М = М1 U М0, где М1 - множество содержащее варианты с выбором первого предмета, М0 – множество, содержащее варианты с отказом от первого предмета.
- оптимальное решение ослабленной задачи на множестве М0 имеют вид х 0* = (0, 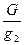 , 0, 0, 0), а оценка этого множества М0 равна
, 0, 0, 0), а оценка этого множества М0 равна

- оптимальное решение вспомогательной задачи на множестве М1:

Это решение дает оценку множества М1 в виде

Полученные оценки множеств М1 и М0 равны, следовательно на этом шаге ветвятся оба множества.
- Продолжим ветвление
множество М0: → М0 = М00  М01
М01
Во множестве М00 – содержатся варианты, в которых первые два предмета в «рюкзак» не взяли.
По правилу выбора решения вспомогательной задачи получим, что на множестве М00:
Х00* = (0,0,  , 0,0) = (0,0,
, 0,0) = (0,0,  , 0,0); оценка
, 0,0); оценка 
Множество М01 включает варианты с отказом от первого предмета и выбором второго. Для него
Х 01* = (0, 1,  , 0, 0) = (0,1,
, 0, 0) = (0,1, 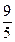 , 0, 0), а оценка
, 0, 0), а оценка
 (х 01*) = 12
(х 01*) = 12 
4. Поскольку полученные оценки для множеств М00 и М01 меньше висячих вершин М1, то переходим на ветвь соответствующую множеством с выбором первого предмета.
Производим ветвление М1: М1 = М11  М10
М10
Для множества М11 имеем:
х 11* = (1, 1,  , 0, 0) = (1, 1,
, 0, 0) = (1, 1, 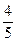 , 0, 0)
, 0, 0)
оценка  (х 11*) = 15
(х 11*) = 15  .
.
Для множества М10 имеет относительное решение вспомогательной задачи х 10* = (1, 0,  , 0, 0) = (1, 0,
, 0, 0) = (1, 0, 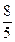 , 0, 0) и оценку
, 0, 0) и оценку  (х 10*) = 15
(х 10*) = 15 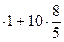 = 31.
= 31.
5. Множество М11 = М110  М111
М111
∙ Для множества М110 имеем решение
х 110* = (1, 1, 0,  , 0) = (1, 1, 0, 1, 0) и оценку
, 0) = (1, 1, 0, 1, 0) и оценку
φ(М110) = f (х 110*) =  .
.
∙ Множество М111 остается, поскольку ему элементы не удовлетворяют ограничению по ресурсам (1)
g1 + g2 + g3 = 14 > 13.
 |
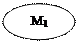


 φ = 39
φ = 39
φ = 39 φ = 39
 | |||||||
 |  |  | |||||



 φ = 26 φ = 30 φ = 31 φ = 35
φ = 26 φ = 30 φ = 31 φ = 35

 ∑gixi > G
∑gixi > G



 φ = 35
φ = 35








 φ = 35 φ = 35
φ = 35 φ = 35
∑gixi > G
φ(М) = f (x *11000) = 27 φ(M) = f (x *11010) = 35
φ(M) = f (x *11001) = 35
f макс = f (х *11001) = f (x *11010) = 35
6. Производим ветвление множества М110 = М1100  М1101
М1101
- Для множества М1100 решение
х *1100 = (1, 1, 0, 0,  ) = (1, 1, 0, 0,
) = (1, 1, 0, 0,  )
)
оценка φ(М1100) = f (x *1100) =  .
.
- Для множества М1101 имеем решение
х *1101 = (1, 1, 0, 1 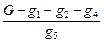 ) = (1, 1, 0, 1, 0) и его оценку φ(М1101) = f (x *1101) =
) = (1, 1, 0, 1, 0) и его оценку φ(М1101) = f (x *1101) =  .
.
7. Поскольку множества М1100 и М1101 имеют одинаковые оценки производим ветвление обоих множеств и просмотрим решения последнего уровня.
М1100 = М11000  М11001 и М1101 = М11010
М11001 и М1101 = М11010  М11011
М11011
- Для множества М11000 решение х *11000 = (1, 1, 0, 0, 0)
оценка φ(М11010) = f (x *11000) = 15 
- Для множества М11001: х *11001 = (1, 1, 0, 0, 1)
оценка φ(М11001) = f (x)*11001) =  .
.
- Множество М11011 – выходит за ограничения по ресурсу
 .
.
Вывод: Задача имеет два оптимальных решения
х* 11011 = (1, 1, 0, 0, 1) и х *11010 = (1, 1, 0, 1, 0), на которых целевая функция f (х *11010) = f (x *11001) = 35.
На оставшихся висячих вершинах значение оценок меньше 35, поэтому других оптимальных решений нет.
Date: 2016-05-14; view: 928; Нарушение авторских прав