Способы выражения состава

Нефтяной газ представлен в виде смеси углеводородов и неуглеводородных компонентов, поэтому для оценки его физико-химических свойств необходимо знать способы выражения состава смеси.

Массовая доля, весовой состав (g_i) i-го компонента – величина, нормированная на 1 в долях или на 100 %. Она характеризует отношение массы i-го компонента (m_i) в системе к общей массе системы:

(2.13)

Молярная доля, мольный состав (N_i) i-го компонента – величина, нормированная на 1 в долях или на 100 %, характеризует отношение числа молей i-го компонента (n_i) к общему числу молей компонентов в системе:

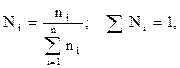
, (2.14)

где m_i – масса i-го компонента;

М_i – молекулярный вес i-го компонента.

Из соотношений (2.13–2.14) легко вывести выражения для пересчётов массового и мольного составов:

[u9]. (2.15)

Объёмная доля i-го компонента – величина, нормированная на 1 или на 100 %, характеризует долю (V_i), которую занимает компонент в объёме системы. С учётом выражений (2.13–2.15) можно показать взаимосвязь объёмной доли с массовой и мольной долями:

. (2.16)

Для идеального газа соблюдается соотношение – объёмная доля компонента (V_i) равна мольной доли компонента (N_i) → V_i = N_i. Этот постулат есть следствие закона Авогадро.

Нефтяной газ рассматривается как идеальная система и его состав можно рассчитать на основе любых данных: масс компонентов, объёмов, плотностей, парциальных давлений и других величин.

Рассмотрим пример.

Дан объёмный состав нефтяного газа (V_i, %): CH₄ – 61,3 %;

C₂H₆ – 15,4 %; C₃H₈ – 12,1 %; ∑C₄H₁₀ – 6,8 %; ∑C₅H₁₂ – 4,4 %.

Найти: какой будет массовый состав (g_i, в долях) газа?

Решение. Для идеального газа величины объёмных (V_i) и мольных (N_i) долей равны. Для расчета состава газа в массовых долях воспользуемся выражением (2.6).

Учитывая молекулярные массы (г/моль) компонентов нефтяного газа: CH₄ – 16; C₂H₆ – 30; C₃H₈ – 44; C₄H₁₀ – 58; C₅H₁₂ – 72, находим: g_CH4 = 61,3·16/(61,3·16 + 15,4·30 + 12,1·44 + 6,8·58 + 4,4·72) =

980,8/2686,4 = 0,365;

g_C2H6 = 15,4·30/2686,4 = 0,172;

g_C3H8 = 12,1·44/2686,4 = 0,198;

g_C4H10 = 6,8·58/2686,4 = 0,147;

g_C5H12 = 4,4·72/2686,4 = 0,118.

Сумма всех долей массового состава равна 1.

Уравнение состояния

Для определения многих физических свойств природных газов используется уравнение состояния.

Уравнением состояния называется аналитическая зависимость между параметрами, описывающими изменение состояние вещества. В качестве таких параметров используются давление, температура, объём. Состояние газа при нормальных и стандартных условиях описывается уравнением Менделеева – Клапейрона:

, (2.17)

где Р – абсолютное давление, Па;

V – объём, м³;

Q – количество вещества, моль;

Т – абсолютная температура, К;

R – универсальная газовая постоянная, Па×м³/(моль×град).

На основе уравнения состояния газа можно рассчитывать многие параметры нефтяного газа: плотность, мольный объём, количество молекул, число молекул, парциальные давления и другие, если рассматривать количество вещества в уравнении состояния газа (2.17), равное 1 молю (Q = 1 моль).

С учётом этого, уравнение состояния газа можно преобразовать следующим образом:

Р·V = ∑N·R·T. (2.18)

Если сумма молей равна единице (∑N = 1 моль), следует, что уравнение приобретает вид Þ Р·V = R·T.

Зная, что масса (m) одного моля идеального газа равна его молекулярной массе (М), умножив левую и правую части на молекулярную массу и массу газа, соответственно, получим:

Р·V·M = m·R·T. (2.19)

Поделив обе части на V·R·T и преобразовав (2.19), получим выражение для расчёта плотности:

Р·M/R·T = m/V, m/V = M·Р/R·T, r = M·Р/R·T. (2.20)

Рассмотрим пример.

Дан один моль метана CH₄.

Найти: какова будет плотность метана при н.у. и с.у.?

Решение. Зная, что молекулярная масса метана равна 16,04 г/моль и один моль метана занимает объём при н.у. 22,414 л, а при с.у. 24,055 л, находим:

r_CH4 (н.у.) = 16,04/22,414 = 0,716 (г/л);

r_CH4 (с.у.) = 16,04/24,055 = 0,665 (г/л).

Из выражения (2.20) и расчётов следует, что плотность газа с возрастанием давления будет расти, а с возрастанием температуры уменьшаться.

Плотность смеси газовых компонентов рассчитывают с учётом средней молекулярной массы смеси газа (M_см) как отношение молекулярной массы смеси газа к его мольному объёму (V_м).

Например, для нормальных условий плотность газа будет рассчитываться по выражению:

r_см = M_см /22,414. (2.21)

Если плотность газа (ρ_о) задана при атмосферном давлении, равном 0,1013 МПа, то пересчёт её величины с учётом другого давления (Р) при той же температуре для идеального газа выполняется по формуле:

r = r_о∙Р/Р_атм. (2.22)

Рассмотрим другой пример.

Плотность метана при н.у. равна 0,716кг/м³. Определить плотность метана (СН₄) при избыточном давлении, например при давлении 500 кПа и температуре 0 °С.

Решение. В этом случае общее давление (1 атм = 101,325 кПа) в системе будет равно Р = (500 + 101,325) = 601,325 кПа.

Зная, что молекулярная масса метана = 16,04 г/моль (кг/кмоль), универсальная газовая постоянная (R) = 8,314 Дж/(К·моль), температура (T) = 273,15 К, находим плотность метана по (2.20 и 2.22):

r_CH4 = Р·М/R·T = 601,325·16,04/8,314·273,15 = 4,25 (кг/м³),

r_CH4 = r_о·Р/Р_ат = 0,716·601,325/101,325 = 4,25 (кг/м³).

Относительная плотность газов величина, рассчитанная по отношению к плотности воздуха, определенного при тех же условиях:

r^о_см = r_см /r_возд. (2.23)

Плотность воздуха (ρ_возд) при н.у. равна» 1,293 кг/м³, а при с.у.» 1,189 кг/м³.

Рассмотрим пример.

Для условий задачи, рассмотренной выше (пример раздела 2.2), рассчитать абсолютные (r) и относительные (ρ^о_см) плотности смеси газов, используя правое выражение (2.12) для расчета молекулярной массы (г/моль):

М_см = 100/(36,5/16 +17,2/30 +19,8/44 +14,7/58 +11,8/72) = 26,874;

r_см = 26,874/22,414 = 1,119 (кг/м³);

ρ^о_см (н.у.) = 1,119/1,293 = 0,927.

Аналогично из (2.20) находится и выражение для мольного объёма:

V = R·T/Р. (2.24)

Мольный объём при давлениях, равных или близких атмосферному и, для физических процессов, когда не происходит изменения числа молей в системе, оценивается соотношением:

V = R·T, (2.25)

где R – универсальна газовая постоянная;

Т – температура, К.

Рассмотрим пример.

Найти вид зависимости изменения мольного объёма газа от температуры → V = f(T).

Решение. Воспользуемся выражением (2.25) и получим объём, занимаемый одним молем идеального газа для условий задачи:

V_н.у. = 0,08206·273,15 = 22,414 (м³,);

V_с.у. = 0,08206·293,15 = 24,055 (м³).

Любой газ при н.у. (Т = 0 ^оС и Р = 100 кПа, 760 мм рт. ст.) занимает объём, равный 22,414 м³, а при с.у. (Т = 20 ^оС и Р = 100 кПа) занимает объём равен 24,055 м³.

С увеличением температуры мольный объём газа увеличивается. Мольный объём газов с возрастанием температуры будет расти, а с возрастанием давления уменьшаться (2.24).

У этого уравнения есть свои граничные условия. Оно справедливо для описания поведения газов при давлениях, близких к атмосферному (от 0,1 до 1,0–1,2 МПа), и при температурах ≈ 0–20 ^оС. При повышенном давлении газ сжимается и его состояние отличается от поведения идеальных газов.

Date: 2016-06-09; view: 2743; Нарушение авторских прав