Методические указания к решению задач контрольной работы

Задачу на равновесие плоской сходящейся системы сил (задачи 1 — 10) следует решить после изучения тем 1.1 и 1.2. В задаче требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В приложены четыре силы, из которых две неизвестны.

Последовательность решения задачи:

1. Выбрать тело (точку), равновесие которого следует рассматри­вать.

2. Освободить тело (шарнир В) от связей и изобразить действую­щие на него активные силы и реакции отброшенных связей. Причем реакции стержней следует направить от шарнира В, так как принято предполагать, что стержни растянуты.

3. Выбрать оси координат и составить уравнения равновесия, используя ус-ловия равновесия системы сходящихся сил на плоскости ΣFιх= 0; ΣFιу= 0.Выбирая оси координат, следует учитывать, что полученные уравнения будут решаться проще, если одну из осей направить перпендикулярно одной из неизвестных сил.

4. Определить реакции стержней из решения указанной системы уравнений.

5. Проверить правильность полученных результатов, решив уравне­ния равновесия относительно заново выбранных координат х₁ и у₁

Пример 1. Определить реакции стержней, удерживающих грузы

F_t = 70 кН и F₂ = 100 кН (рис. 1,а). Массой стержней пренебречь.

Решени е. I. Рассматриваем равновесие шарнира В (рис.1,а)

2.Освобождаем шарнир В от связей и изображаем действующие на него активные силы F_1, F_2.

3.Заменим связи их реакциями R _1, R₂

4.Выбираем систему координат, совместив ось у по направлению R₂ (рис.1,б) и составляем уравнения равновесия для системы сил, действующих на шарнир В:

∑ F_ix = F₂∙cos 30^o – R₁∙ cos45^o = 0 (1)

∑ F_iy = -F₁ + F₂ ∙cos60^о+ R₂ + R₁∙ cos45^о = 0 (2)

5. Определяем реакции стержней R₁ и R₂ , кН:

Из уравнения (1)

Подставляя найденное значение R₁ в уравнение (2), получаем

Знак минус перед значением R₂ указывает на то, что первоначально выбранное направление реакции неверное — следует направить реак­цию R₂ в противоположную сторону, т.е. к шарниру В (на рис. 1,б истинное направление реакции R₂ показано штриховым вектором).

6. Проверяем правильность полученных результатов, выбрав новое расположение осей координат Χ_1, Υ₁(рис. 1, в). Относительно этих осей составляем уравнения равновесия:

ΣF_ix1= — R₂ ∙ cos 45° + F₂ ∙ соs 15° — F₁∙ cos 45° = 0, (3)

Σ F _{i y1} = R₁ — F₁∙cos45°— R₂∙cos45° — F₂ ∙cos75° = 0. (4) Из уравнения (3) находим

Подставляя найденное значение R₂ в уравнение (4), получаем

R₁ = 70∙ 0,707 + 66,6∙ 0,707 + 100 ∙0,258 = 122 kH

Значения реакций R₁ и R₂, полученные при решении уравнений (1) и (2), совпадают по величине и направлению со значениями, найденными из уравнений (3) и (4), следовательно, задача решена правильно.

Задачу на равновесие плоской произвольной системы сил (задачи 11—20) следует решать после изучения тем 1.3 и 1.4. Во всех задачах требуется определить реакции опор балок. Студентам необходимо приобрести навыки определения реакций опор, так как с этого начинается решение многих задач по разделу «Сопротив­ление материалов».

Последовательность решения задачи:

1. Изобразить балку вместе с нагрузками. Выбрать положение координатных осей, совместив ось х с балкой, а ось у направив перпендикулярно оси х.

2. Произвести необходимые преобразования за­данных активных сил: силу, наклоненную к оси балки под углом α, заме­нить двумя взаимно пер­пендикулярными состав­ляющими, а равномерно распределенную нагруз­ку — ее равнодействую­щей, приложенной в середине участка действия равномерно распределенной нагрузки.

3.Освободить балку от опор, заменив их действие реакциями опор, направленными вдоль выбранных осей координат.

4.Составить уравнения равновесия статики для произвольной плоской системы сил, таким образом, и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор. Проверить правильность найденных опорных реакций по уравнению, которое не было использовано для решения задачи.

Пример 2. Определить реакцию опор балки (рис. 2, а).

Решение1. Изобразим балку с действующими на нее нагруз­ками(рис.2 а).

2. Изображаем оси координат х и у.

3. Силу F заменяем ее составляющими F_x = F∙ cos αи F_y = F ∙sin α. Равнодействующая q ∙ CD равномерно распределенной на­грузки приложена в середине участка CD в точке К и имеет направление нагрузки.(рис. 2,б).

4.Освобождаем балку от опор, заменив их опорными реакциям (рис. 2, в).

5. Составляем уравнения равновесия статики и определяем не­известные реакции опор.

Из уравнения суммы моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:

Определяем другую вертикальную реакцию:

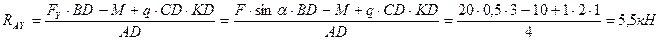
Определяем горизонтальную реакцию:

ΣF _ix=R_Ax-F_x=0; R_Ax=F_x=Fcosα=20∙0,866=17, 3 кН

6.Проверяем правильность найденных результатов:

ΣF_iу = R_ay – F_y –qCD +R_Dy =5,5-20 -2 +6,5 = 0

Условие равновесия ΣF_iу = 0 выполняется, следовательно, реакции опор определены верно.

Задачу на равновесие пространственной произвольной системы сил (задачи 21—30) следует решать после изучения, темы 1.5.

Последовательность решения задачи:

1.Изобразить на рисунке тело, равновесие которого рассматривается, с действующими на него активными силами и реакциями опор и выбрать систему осей координат.

2.Из условия равновесия вала, имеющего неподвижную ось, определить значение силы F₂, после чего вычислить значение силы F_{r 2}

3.Составить шесть уравнений равновесия. Решить уравнения и определить реакции опор.

4. Проверить правильность решения задачи.

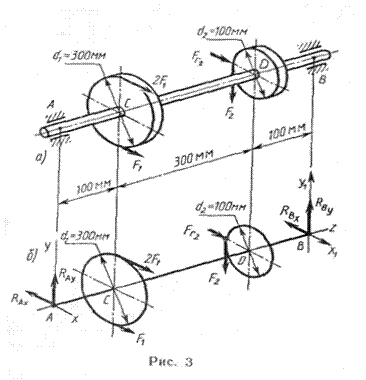
Пример 3. На вал (рис. 3, а) жестко насажены шкив 1 и колесо 2. Определить силы F_2, F_r2 =0,4 F₂, а также реакции опор А и В, если F₁=100 Н

Решение. I. Изображаем вал со всеми действующими на него силами, а также оси координат (рис. 3,б).

2. Определяем F₂ и F_2r. Из условия равновесия вала, имеющего неподвижную ось: ; ;

;

4. Составляем шесть уравнений равновесия:

;;

4.Решаем уравнения (1), (2), (3), (4) и определяем реакции опор:

из (1) ;

из (2) ;

из (3) ;

из (4) .

5.Проверяем правильность найденных реакций опор. Используем уравнение (5):

,

∑Χ_ι =0; следовательно, реакции R_Ay и R_Bx определены верно.

Используем уравнение (6):

_,

_, следовательно_, реакции R_Ay и R_By определены верно.

Данную задачу можно решать другим методом: спроектировать тело со всеми действующими на него активными силами и реакциями опор на три координатные плоскости, чтобы проще было составлять уравнения равновесия.

Задачи 31—40 требуют от студентов умения строить эпюры продоль-ных сил, нормальных напряжений и определять удлинение или укороче-ние бруса. К решению данной задачи следует приступать после изучения темы 2.2.

При работе бруса на растяжение и сжатие в его поперечных сече­ниях возникает продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, действующих на отсеченную часть.

N= ∑ F_{iz ост.ч.}

Правило знаков для N: при растяжении продольная сила поло-жительна, при сжатии — отрицательна.

При растяжении (сжатии) бруса в его поперечных сечениях возни­кают нормальные напряжения σ= N /А (А — площадь поперечного сечения). Для нормальных напряжений принимается то же правило знаков, что и для продольных сил.

Изменение длины бруса (удлинение или укорочение) равно алгебраи-ческой сумме удлинений (укорочений) его отдельных участков и вы-числяется по формуле Гука:

где N_i, l_i, A_i, — соответственно продольная сила, длина и площадь сечения в пределах каждого участка бруса; E — модуль продольной упругости.

Последовательность решения задачи:

1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, и места изменения размеров поперечного сечения.

2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N), построить эпюру продольных сил N. Проведя па-раллельно оси бруса базовую (нулевую) линию эпюры, отложить пер-пендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, перпендикулярно базовой линии.

3. Для построения эпюры нормальных напряжений определить напря-жения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т. е. эпюра на данном участке изображается прямой, параллельной оси бруса.

4. Перемещение свободного конца бруса определяем как сумму удли-нений (укорочений) всех участков бруса, вычисленных по формуле Гука.

Пример 4. Для данного ступенчатого бруса (рис. 4, а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если

Дано: Е=2-10⁵МПа;

F₁= 30кH =30 10³ H; F₂ = 38∙10³ H; F₃ = 42 кН = 42∙ 10³ Н;

А₁ = 1,9 см² = 1,9 ∙ 10² мм²; А₂ = 3,1 см² = 3,1∙ 10² мм².

Решение.

1. Отмечаем участки, как показано на рис.4,а.

2.Определяем значения продольной силы N на участках бруска:

N₁ = 0;

N_II= F₁ = 30 кН;

N_III = F₁ = 30 кН;

N_IV = F₁ – F₂ = – 8 кН;

N_V = F₁ – F₂– F₃ = – 50кН.

3.Строим эпюру продольных сил (рис.4,б)

4.Вычисляем значения нормальных напряжений: рис.4

5.Строим эпюру нормальных напряжений (рис.4,в).

6.Определяем перемещение свободного конца:

Брус удлиняется на Δ ℓ = 0,23 мм.

Решение задач 41 —50 требует знаний методики прочностных и жесткостных расчетов при кручении, поэтому к решению этой задачи следует приступить после изучения темы 2.4.

Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор — крутящий момент М_к (или М_z).

Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих на отсеченную часть: M_K=ΣMi_z (имеется в виду, что плоскости действия всех внешних скручивающих моментов М, перпендикулярны продольной оси бруса).

Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке. Соответствующий внешний момент направлен против часовой стрелки (рис.5).

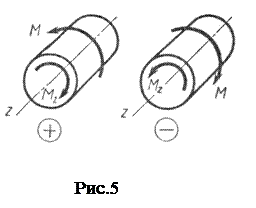В пятой задаче необходимо выполнить проектный расчет вала круглого или кольцевого поперечно-го сечения из условий прочности и из условий жесткости; из двух полу-ченных значений диаметров следует выбрать наибольшее значение.

Последовательность решения задачи:

1. Определить внешние скручивающие моменты по формуле

М = Р/ω,

где Р — мощность, Вт

ω — угловая скорость с^-1.

2. Определить уравновешивающий момент, используя уравнение рав-новесия ΣМ_iz = 0, так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) момен-тов равна нулю.

3.Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала.

4.Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала круглого или кольцевого сечения из условия прочности и жесткости. Для кольцевого сечения вала принять соотношение диаметров α =do/d, где d ₀ — внутренний диаметр кольца; d — наружный диаметр кольца.

Из условия прочности:	Из условия жесткости:
где Мz max — наибольший крутя­щий момент; Wp — полярный момент сопро­тивления поперечного сечения; [τк] — допускаемое касательное напряжение	где Ip — полярный момент инер­ции сечения; G — модуль сдвига; [φ0] — допускаемый относи-тельный угол закручивания сечения
Сечение вала — круг
Необходимый для обеспечения прочности диаметр вала	Необходимый для обеспечения жесткости диаметр вала
Сечение вала — кольцо
Необходимый наружный диаметр кольца для обеспечения прочности     Внутренний диаметр кольца	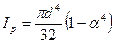Необходимый наружный диаметр кольца для обеспечения жесткости   Внутренний диаметр кольца

Пример 5. Для стального вала (рис.6,а) постоянного по длине сечения требуется:

1) определить значения моментов М₂ и М₃, соответствующие передаваемым мощностям Р₂ и Р₃, а также уравновешиваюший момент М_1;

2) построить эпюру крутящих моментов;

3) определить требуемый диаметр вала из расчетов на прочность и жесткость, полагая по варианту (а) поперечное сечение вала — круг; по варианту (б) — поперечное сечение вала — кольцо, имеющее соотношение диаметров. Окончательное значение диаметра округлить до ближайшего четного (или оканчивающегося на пять) числа.

Дано: Р₂ = = 52 кВт

Р₃ =50 кВт;

ω = 20 рад/с;

α = do/d = 0,8.

[τ_к]=30 МПа;

[φ₀] = 0,02рад/м = 0,02-10^-3 рад/мм;

G = 8∙10⁴ МПа

Решение.

1. Определяем внешние скручивающие моменты:

2. Определяем уравновешивающий момент M_i:

ΣМ_iz=0; M₁ - M₂-M₃=0;

М₁= М₂ + М₃ = 5100Нм

3. Определяем крутящий момент по участкам вала:

M_zI=M₁ = 5100Нм;

M_zII=M₁ –M₂₌ 5100-2600 = 2500Нм.

Строим эпюру крутящих моментов Э М_z (рис. 6,б).

4. Определяем диаметр вала из условий прочности и жесткости:

М_{z max}=5100Нм (рис. 14,б).

а) Сечение вала — круг

Из условия прочности:

:

Из условия жесткости:

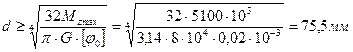
Требуемый диаметр получился больше из расчета на прочность, поэтому его принимаем как окончательный d = 95 мм.

б) Сечение вала - кольцо

Из условия прочности: Из условия жесткости:

Принимаем d = 114 мм. Принимаем d =86мм.

Требуемые диаметры окончательно принимаем из расчетов на прочность:

d=114мм; d_o = 0,8d = 0,8∙114 = 91,2 мм. Принимаем d_o = 92 мм.

К решению задач (51—60) сле­дует приступить после изучения темы 2.5 «Изгиб». Изгиб — это такой вид нагружения бруса, при котором в его поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы; такой изгиб называют поперечным: если поперечные силы не возникают, изгиб называют чистым. Изгибающий момент М_нов произвольном поперечном сечении бруса численно равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относительно центра тяжести сечения:

M_но = ΣM_сеч(F_{i ост. ч.}). Поперечная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на отсеченную часть:

Q = Σ F_{iост. ч.}. Причем все внешние силы и моменты действуют в главной продольной плоскости бруса и расположены перпендикулярно продольной оси бруса.

Правило знаков для поперечной силы: силам, поворачивающим отсеченную часть балки относительно рассматриваемого сечения по ходу часовой стрелки, приписывается знак плюс (рис. 7,а), а силам, поворачивающим отсеченную часть балки относительно рассматриваемого сечения против хода часовой стрелки, приписывается знак минус (рис. 8, б).

Правило знаков для изгибающих моментов: внешним моментом, изгибающим мысленно закрепленную в рассматриваемом сечении отсеченную часть бруса выпуклостью вниз, приписывается знак плюс (рис. 8, а), а моментам, изгибающим, отсеченную часть бруса выпуклостью вверх — знак минус (рис. 8,б).

На основе метода сечений достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями. Характерными являются сече-ния балки, где приложены сосредоточенные силы и моменты (включая опор-ные реакции), а также сечения, ограничивающие участки с равномерно расп-ределенной нагрузкой.

Приведем некоторые правила построения эпюр.

Для эпюры поперечных сил:

1. На участке, нагруженном равномерно распределенной нагрузкой, эпюра изображается прямой, наклоненной к оси балки.

2. На участке, свободном от действия распределенной нагрузки, эпюра изображается прямой, параллельной оси балки.

3. В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не изменяет своего значения.

4. В сечении, где приложена сосредоточенная сила, значение по-перечной силы меняется скачкообразно на величину, равной модулю прило-женной силы.

5. В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сече-нии. Если в концевом сечении балки не приложена сосредоточенная сила, то поперечная сила в этом сечении равна нулю.

Для эпюры изгибающих моментов:

1. На участке, нагруженном равномерно распределенной нагрузкой, эпюра моментов изображается квадратичной параболой. Выпуклость па-раболы направлена навстречу нагрузке.

2. На участке, свободном от действия равномерно распределенной наг-рузки, эпюра моментов изображается прямой линией.

3. В сечении балки, где приложена сосредоточенная пара сил, изгибающий момент меняется скачкообразно на значение, равное моменту приложенной пары.

4. Изгибающий момент в концевом сечении балки равен нулю, если в нем не приложена сосредоточенная пара сил. Если же в концевом сече-нии приложена активная или реактивная пара сил, то изгибающий момент в сечении равен моменту приложенной пары.

5. На участке, где поперечная сила равна нулю, балка испытывает

чистый изгиб, и эпюра изгибающих моментов изображается прямой,

параллельной оси балки.

6. Изгибающий момент принимает экстремальное значение в сечении, где эпюра поперечных сил проходит через ноль, меняя знаки с «+» на «—» или с «—» на «+».

В рассматриваемой задаче требуется построить эпюры поперечных сил и изгибающих моментов, а также определить размеры поперечного сечения балки в форме прямоугольника и круга.

Условие прочности для балок с сечениями, симметричными относительно нейтральной оси, имеет вид:

где W_х —осевой момент сопротивления сечения.

Из условия прочности определяют значение осевого момента сопротивления:

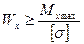
По найденному моменту сопротивления W определяют размеры поперечного сечения.

Последовательность решения задачи:

1.Определить реакции связей.

2 Балку разделить на участки по характерным сечениям.

3. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил.

4. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов.

5. Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т. е. определить W_х в опасном сече-нии, где изгибающий момент имеет наибольшее по модулю значение.

6.По величине W_x, в зависимости от формы поперечного сечения, опре-делить размеры поперечного сечения.

Пример6. Для заданной двух опорной балки (рис. 9, а) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения (h, b, d) в форме прямоугольника или круга, приняв для прямоугольника h/b = 1,5. Считать [σ] = 160 МПа.

Решение.

1. Определяем опорные реакции и проверяем их найденные значения:

ΣM_D = 0; -M₁ + F₂∙CD + M₂ + R_B∙BD – F₁∙OD=0;

Так как реакция R_D получилась со знаком минус, то изменяем ее перво-начальное направление на противоположное. Истинное направление реакции R_D — вниз (рис. 18, б).

Проверка: Σ F _iy= - F +R_B + F₂ - R_D = - 18 + 10 + 30 - 22 = 0.

Условие Σ F_iy = 0 выполняется, следовательно, реакции опор определены верно. При построении эпюр используем только истинные направления реакций опор.

2. Делим балку на участки по характерным сечениям О, В, С, Д (рис. 9,б).

3. Определяем в характерных сечениях значения поперечной силы Q_y и строим эпюру слева направо (рис. 9, в):

Q_у = -F₁ = -18кН;

Q_у = -F ₁ = - 18кН;

Q_у = - F+R_B= - 18+10= - 8кН;

Q_у = - F+R_B= - 18+10= - 8кН;

Q_у = - F₁+R_B+F₂= - 18+10 + 30= 22 кН;

Q_у = - F₁+R_B+F₂= 22 кН;

4. Вычисляем в характерных сечениях значения изгибающего мо­мента М_х и строим эпюру (рис. 9, г):

М_хА = 0:

М_хB = - F ∙ АВ = - 18∙5= - 90кНм;

M_х = -F∙OC+R_B∙ BC = - 18 ∙ 9 + 10 ∙ 4 = - 122 кНм;

M_х = - F₁ ∙ OC + R_B ∙ BC +M₂ = - 18 ∙ 9 + 10 ∙ 4 +10 = -112кНм;

M_х = - F₁ ∙ OD + R_B ∙ BD +M₂ + F₂ ∙ CD = - 18 ∙ 15 + 10 ∙ 10 +10 +10 + 30 ∙ 6 = =20кНм

5.Для наиболее опасного сечения определяем величину осевого момента сопротивления поперечного сечения из условия прочности на изгиб:

5. Вычисляем размеры сечения данной балки по двум вариантам:

а ) сечение — прямоугольник с заданным соотношением сторон

Используя формулу и учитывая, что h=1,5b, находим

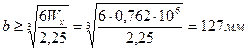
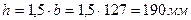
б ) сечение — круг

Используя формулу , находим диаметр круглого сечения

Для решения задач (61-70) необходимо усвоить тему 2.6 «Сочетание основных видов деформаций», т.к. в задачах(61-70) рассматривается совмест-ное действие кручения и изгиба и расчет проводится с использованием одной из гипотез прочности.

Условие прочности в этом случае имеет вид

где M_экв —эквивалентный момент.

По гипотезе наибольших касательных напряжений (иначе—третья гипотеза)

По гипотезе потенциальной энергии формоизменения (иначе — пятая гипотеза)

В обеих формулах М_к и М_и — соответственно крутящий и суммарный изгибающий моменты в рассматриваемом сечении вала. Числовое значение суммарного изгибающего момента равно геометрической сумме изгибающих моментов, возникающих в наиболее опасном сечении от вертикально и горизонтально действующих внешних сил, т. е.

Последовательность решения задачи:

1. Привести действующие на вал нагрузки к его оси, освободить вал от опор, заменив их действие реакциями в вертикальной и горизон­тальной плос-костях.

2. По заданной мощности Р и угловой скорости w определить вращаю-щие моменты, действующие на вал.

3. Вычислить нагрузки F₁, F_r1, F₂, F_r2, приложенные к валу.

4. Составить уравнения равновесия всех сил, действующих на вал, от-дельно в вертикальной плоскости и отдельно в горизонтальной плоскости и определить реакции опор в обеих плоскостях

5. Построить эпюру крутящих моментов.

6. Построить эпюры изгибающих моментов в вертикальной и горизон-тальной плоскостях (эпюры Э М_x и ЭM_v).

7. Определить наибольшее значение эквивалентного момента в наиболее опасном сечении:

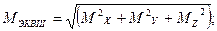
8. Определить осевой момент сопро­тивления:

9.Проверить прочность вала по одной из гипотез прочности, используя условие прочности при изгибе

Пример 7. Стальной вал постоянного поперечного сечения, диаметром d=60мм, с двумя зубчатыми колесами (рис. 19, а), передает мощность Р =15кВт при угловой скорости ω=30рад/с.

Проверить прочность вала по двум вариантам:

а) используя третью гипотезу прочности;

б) исполь­зуя пятую гипотезу прочности, сделать вывод о рациональности назначенного размера поперечного сечения, приняв: [σ] = 160 МПа; F_r1=0,4F₁ F_r2=0,4F₂

Решение.

1. Составляем расчетную схему вала, приводя дейст­вующие на вал нагрузки к оси (рис. 10,б). При равномерном вращении вала M₁= М₂, где М₁ и М₂ - моменты скручивающих пар, которые добавля­ются при переносе сил F₁ и F₂ на ось вала. 2.Определяем вращающий момент, действующий на вал:

3.Вычислим нагрузки, приложенные к валу:

4. Определяем реакции опор в вертикальной плоскости:

ΣY = 0, следовательно, R_Aу и R_By найдены правильно.

Определяем реакции опор в горизонтальной плоскости (рис. 10, б)

Знак минус указывает, на то, что истинное направление реакции противоположно выбранному (рис. 10, б):

ΣX = 0, следовательно, R_AХ, и R_Bх, найдены верно.

5.Строим эпюру крутящих моментов М_z (рис. 19, в).

М_Z =М₁ =0,5кНм

6.Определяем в характерных сечениях значения изгибающих моментов М_х в вертикальной плоскости и М_у в горизонтальной плоскости и строим эпюры ЭМ_х,ЭМ_у:

M_Cx=R_Ay∙AD=3,6∙0,005=0,18кНм;

М_Dx=R_Ay∙AD-F_r1∙CD=3,6∙0,25-4∙0,2=0,1 кНм;

M_Cy=R_Ax∙AC=7,66∙0,05=0,383 кНм;

M_Dy=R_Ax∙AD-F₁∙CD=7,66∙0,25-10∙0,2=-0,085 кНм;

7. Вычисляем наибольшее значение эквивалентного момента по заданным гипотезам прочности. Так как в данном примере значение суммарного изгибающего момента в сечении С больше, чем в сечении D

то сечение С и является опасным. Определяем эквивалентный мо-мент в сечении С.

Вариант а) по гипотезе максимальных касательных напряжений

Вариант б) по гипотезе удельной энергии формоизменения

8. Определяем осевой момент сопротивления поперечного сечения

9.Проверяем прочность вала:

по варианту а)

^{Вывод: прочность вала обеспечена, но диаметр вала завышен, т.к. имеет место большая недогрузка.}

по варианту б)

^{Вывод: прочность вала обеспечена, но диаметр вала завышен, т.к.имеет место большая недогрузка.}