Решение типовых заданий

Типовые задания 1 – 5 предназначены длястудентов дневной и заочной

(полной) форм обучения для всех специальностей; типовые задания 1–6

предназначены длястудентов заочнойсокращенной формы обучения для

всех специальностей.

При решении типовых заданий 1 – 5 студенты дневного отделениядолжны использовать методические пособия [1]–[8], а студенты заочной

(полной) формы обучения – методические пособия [9]–[15]; при решении типовых заданий 1 – 6 студенты заочной сокращенной формы обучения должны использовать методические пособия [9]–[16].

1. Вычислить определенный интеграл , применяя подходя-

щую подстановку.

Решение. Сделаем подстановку 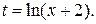Находим:

Тогда искомый интеграл преобразуется к виду:

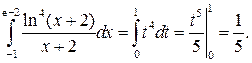
2. Вычислить площадь плоской области , ограниченной линиями

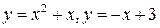. Построить область .

Решение. Строим график функции 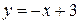(прямая). Находим: Строим график функции 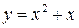(парабола). Находим нули параболы: 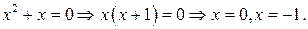Так как , то ветви параболы направлены вверх (рис. 1). Находим точки пересечения графиков функций:

Тогда площадь плоской области вычисляется с помощью определенного интеграла:

Рис.1.

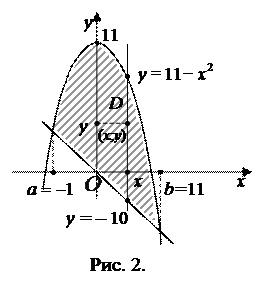
3. Вычислить площадь фигуры , ограниченной линиями

, .

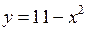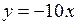Решение. Область интегрирования

(рис. 2) ограничена сверху параболой 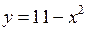, а снизу прямой 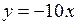. Пределы интегрирования 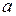и 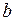определяются из системы уравнений:

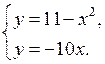
Отсюда получаем уравнение: или , которое имеет корни 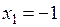, . Таким образом, пределы интегрирования 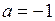, 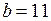. Тогда площадь плоской области вычисляется с помощью определенного интеграла:

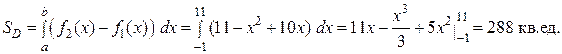
4. Найти частные производные 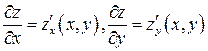функции двух переменных 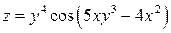и записать ее полный дифференциал.

Решение. Используя правила дифференцирования, таблицу производ-

ных и считая 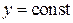, находим частную производную :

Теперь, считая 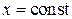и используя правила дифференцирования и таблицу производных, находим частную производную :

5. Найти частное решение (или частный интеграл) дифференциального уравнения первого порядка 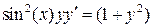, удовлетворяющее заданному начальному условию 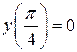(решить задачу Коши).

Решение. Производную представим в дифференциальной форме: .

Тогда искомое дифференциальное уравнение – уравнение с разделяющи-

мися переменными, запишется в виде

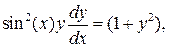
которое после разделения переменных, принимает вид:

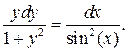
Отсюда, интегрируя, находим решение в виде общего интеграла:

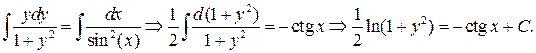
Используя начальное условие 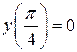находим значение постоянной

интегрирования:

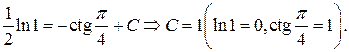
Тогда частный интеграл дается выражением:

6. Найти частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами , удовлетворяющее заданным начальным условиям 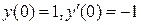(решить задачу Коши).

Решение. 1) Вначале находим общее решение однородного дифференциального уравнения 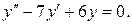Его решения ищем в виде 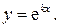Находим: 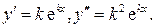Подставляя эти значения в однородное дифференциальное уравнение получим характеристическое уравнение: 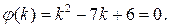Его корни могут быть найдены по формулам корней квадратного уравнения (см. пример 2): 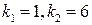, каждый кратности 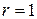. Следовательно, есть частные решения однородного дифференциального уравнения. Тогда общее решение однородного дифференциального уравнения представится в виде линейной комбинации этих частных решений с произвольными постоянными:

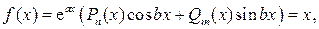2) Частное решение линейного неоднородного дифференциального уравнения будем искать по виду его правой части где 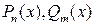– многочлены степени соответственно. Сравнивая выражения в левой и правой частях последнего равенства, находим значения параметров 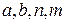, при которых они совпадают: 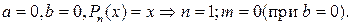Частное решение для линейных неоднородных дифференциальных уравнений с постоянными коэффициентами определяется по виду его правой части :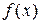

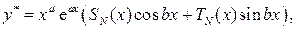
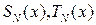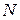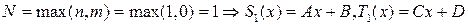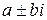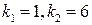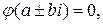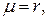где – многочлены степени с неопределенными коэффициентами, , а параметр определяется из условия сравнения комплексного числа с корнями характеристического уравнения а именно, если то где 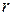– кратность корня если же то 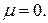Отсюда следует:

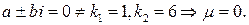
Таким образом, 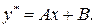Подставляя в линейное неоднородное дифференциальное уравнение и приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства, приходим к системе уравнений для нахождения значений параметров :

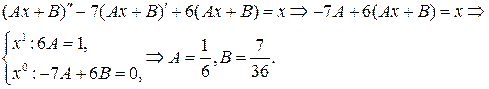
Следовательно, .

3) Общее решение неоднородного дифференциального уравнения представляется в виде суммы решений :

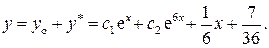
4) Используя начальные условия 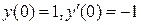, находим значения по-

стоянных интегрирования:

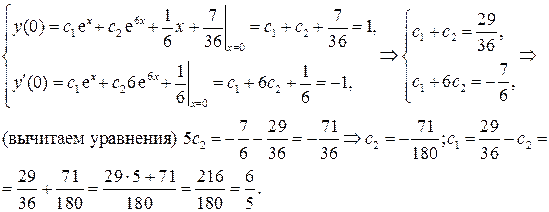
Следовательно, частное решение исходного линейного неоднородного

дифференциального уравнения второго порядка с постоянными коэффи-

циентами , удовлетворяющее заданным начальным усло-

виям 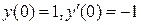, дается выражением:

7. Найти частное решение линейного неоднородного дифференциального

уравнения второго порядка с постоянными коэффициентами , удовлетворяющее заданным начальным условиям

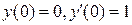(решить задачу Коши).

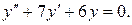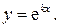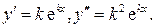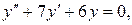Решение. 1) Вначале находим общее решение однородного дифференциального уравнения Его решения ищем также в виде Находим: Подставляя эти значения в однородное дифференциальное уравнение получим характеристическое уравнение: 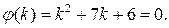Его корни могут быть найдены по формулам корней квадратного уравнения (см. пример 2): 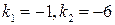, каждый кратности 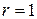. Следовательно,

есть частные решения однородного дифференциального уравнения. Тогда общее решение однородного дифференциального уравнения представится в виде линейной комбинации этих частных решений с произвольными постоянными:

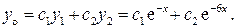
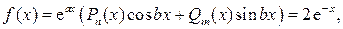2) Частное решение линейного неоднородного дифференциального уравнения будем искать по виду его правой части где 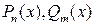– многочлены степени соответственно. Сравнивая выражения в левой и правой частях последнего равенства, находим значения параметров 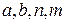, при которых они совпадают: 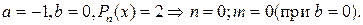Частное решение для линейных неоднородных дифференциальных уравнений с постоянными коэффициентами определяется по виду его правой части :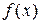

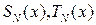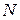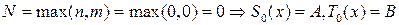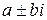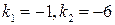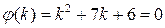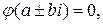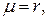где – многочлены степени с неопределенными коэффициентами, , а параметр определяется из условия сравнения комплексного числа с корнями характеристического уравнения , а именно, если то где 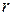– кратность корня если же то 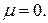Отсюда следует:

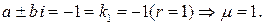
Таким образом, 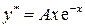Подставляя 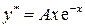в линейное неоднородное дифференциальное уравнение и приравнивая коэффициенты при одинаковых функциях в левой и правой частях полученного равенства, приходим к системе уравнений для нахождения значения параметра :

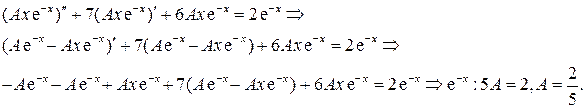
Следовательно, .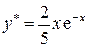

3) Общее решение неоднородного дифференциального уравнения представляется в виде суммы решений :

4) Используя начальные условия 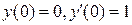, находим значения по-

стоянных интегрирования:

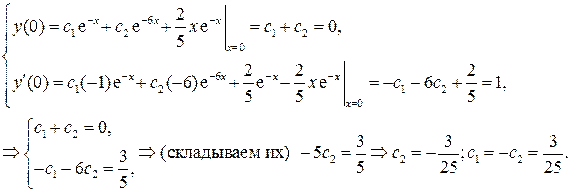
Следовательно, частное решение исходного линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами , удовлетворяющее заданным начальным условиям 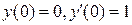дается выражением:

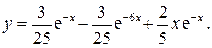
8. Найти область сходимости функционального ряда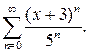

Решение. 1) Фиксируем из области сходимости функционального ряда.

Тогда функциональный ряд 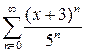становится знакопеременным схо-

дящимся числовым рядом. Исследуем его на абсолютную сходимость. Для

этого рассмотрим ряд из модулей и исследуем его на сходи-

мость с помощью радикального признака Коши:

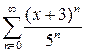есть область, где ряд из модулей сходится, а, следовательно, исходный функциональный ряд в области 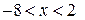сходится абсолютно.

2) Исследуем исходный функциональный ряд 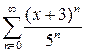на сходимость в граничных точках 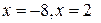его области сходимости. При исходный функциональный ряд 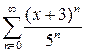становится знакочередующимся числовым рядом 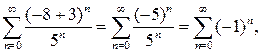который расходится, так как 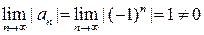(следствие из необходимого признака сходимости числового ряда). При 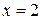исходный функциональный ряд 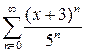становится знакоположительным числовым рядом 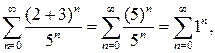который также расходится по следствию из необходимого признака сходимости числового ряда ().

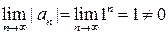Итак, 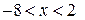– область сходимости исходного функционального ряда.

9. Найти область сходимости функционального ряда .

Решение. 1) Фиксируем из области сходимости функционального ряда.

Тогда функциональный ряд становится знакопеременным

сходящимся числовым рядом. Исследуем его на абсолютную сходимость.

Для этого рассмотрим ряд из модулей 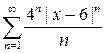и исследуем его

на сходимость с помощью признака Даламбера:

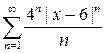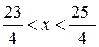есть область, где ряд из модулей сходится, а, следовательно, исходный функциональный ряд в области сходится абсолютно.

2) Исследуем исходный функциональный ряд на сходимость в граничных точках его области сходимости. При исходный функциональный ряд становится знакочередующимся числовым рядом , который исследуем на абсолютную сходимость. Для этого рассмотрим ряд из модулей 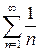и исследуем его на сходимость. Числовой ряд 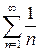–гармонический ряд, который расходится. Следовательно, знакочередующийся числовой ряд не является абсолютно сходящимся. Исследуем его на условную сходимость с помощью признака Лейбница. Проверяем условия признака Лейбница:

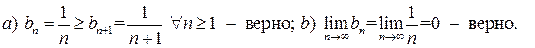
Следовательно, знакочередующийся числовой ряд сходится условно в точке .

При исходный функциональный ряд становится гармоническим рядом , который расходится.

Итак, 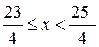– область сходимости исходного функционального ряда.

Литература

Дневное отделение

[1]. Авакян Е.З., Иванейчик И.В. Практическое пособие к домашним заданиям по дисциплине «Высшая математика», раздел «Неопределенный и определенный интегралы», № 2506, 2000 г.

[2]. Евтухова С.М., Иванейчик И.В. Практикум по выполнению расчетно-графических работ по теме «Неопределенный и определенный интегралы», № 3908, 2009 г.

[3]. Курлович С.П., Иванейчик И.В., Дегтярева Е.А. Практикум «Функции нескольких переменных» по выполнению домашних заданий по курсам «Математика» и «Высшая математика», № 3527, 2007 г.

[4]. Великович Л.Л., Черниченко Ю.Д. Учебное пособие «Математический анализ. Функции нескольких переменных» по дисциплинам «Высшая математика» и «Математика» для студентов дневной и заочной форм обучения на электронном носителе, 2012 г.

[5]. Черниченко Ю.Д., Трюхан Н.А., Гойко В.И. Практическое руководство к расчетно-графическим работам по дисциплине «Высшая математика», раздел «Дифференциальные уравнения», № 2411, 1999 г.

[6]. Черниченко Ю.Д., Трюхан Н.А., Гойко В.И. Практикум к расчетно-графическим работам по дисциплине «Высшая математика», раздел «Дифференциальные уравнения», № 2389, 1999 г.

[7]. Зыкунов В.А., Черниченко Ю.Д. Практическое пособие к домашним заданиям по дисциплине «Высшая математика», раздел «Дифференциальные уравнения», № 2519, 2001 г.

[8]. Тимошин С.И. Пособие «Дифференциальные уравнения и их приложения» для студентов технических ВУЗов, № 3060, 2005 г.

Заочное отделение

[9]. Вальковская В.И., Лашкевич В.И. Пособие по дисциплине «Математика» для студентов инженерно-технических специальностей заочной формы обучения, раздел «Интегральное исчисление функции одной переменной», № 4002, 2010 г.

[10]. Авакян Е.З., Иванейчик И.В. Практическое руководство «Функции нескольких переменных и интегральное исчисление» к контрольным заданиям по дисциплине «Высшая математика», № 2746, 2002 г.

[11]. Авакян Е.З., Иванейчик И.В. Практикум «Функции нескольких переменных и интегральное исчисление» к контрольным заданиям по дисциплине «Высшая математика», № 2724, 2002 г.

[12]. Авакян С.Л., Авакян Е.З., Черниченко Ю.Д. Практическое пособие «Дифференциальные уравнения. Ряды. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля» к контрольным заданиям по дисциплинам «Высшая математика» и «Математика» для студентов заочного отделения инженерно-технических специальностей, часть 3, № 2949, 2004 г.

[13]. Авакян С.Л., Авакян Е.З., Черниченко Ю.Д. Практикум «Дифференциальные уравнения. Ряды. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля» к контрольным заданиям по дисциплинам «Высшая математика» и «Математика» для студентов заочного отделения инженерно-технических специальностей, часть 3, № 2816, 2003 г.

[14]. Гойко В.И., Курлович С.П., Тепляков В.Г. Практическое руководство «Ряды. Дифференциальные уравнения» по курсу «Высшая математика» для студентов экономических специальностей заочной формы обучения, № 3494, 2007 г.

[15]. Гойко В.И., Курлович С.П., Тепляков В.Г. Практикум «Ряды. Дифференциальные уравнения» к контрольным работам по курсу «Высшая математика» для студентов экономических специальностей заочной формы обучения, № 3495, 2007 г.

[16]. Черниченко Ю.Д., Емелин А. В. Курс лекций «Ряды. Кратные, криволинейные и поверхностные интегралы. Элементы теории поля», часть 1 по дисциплинам «Высшая математика» и «Математика» для студентов дневной и заочной форм обучения, в том числе и на электронном носителе, № 3993, 2010 г.

Составил: доцент Черниченко Ю.Д.

Date: 2016-06-08; view: 525; Нарушение авторских прав