
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Игра двух лиц с нулевой суммой
|
|
Методы теории игр наиболее развиты для конечной одноходовой игры двух лиц с нулевой суммой (т.е. сумма выигрышей игроков равна 0). Такие игры еще называют антагонистическими.
Пусть  и
и  – участники игры. Саму игру опишем с помощью так называемой платежной матрицы (матрицы игры) порядка
– участники игры. Саму игру опишем с помощью так называемой платежной матрицы (матрицы игры) порядка  . Строки этой матрицы – это чистые стратегии игрока
. Строки этой матрицы – это чистые стратегии игрока 
 , а столбцы – чистые стратегии игрока
, а столбцы – чистые стратегии игрока 
 /
/
Предполагается, что каждому игроку известны все элементы платежной матрицы.
Элемент  определяет результат игры, а именно выигрыш игрока
определяет результат игры, а именно выигрыш игрока  при выборе игроками
при выборе игроками  и
и  стратегий
стратегий  и
и  соответственно.
соответственно.
В этом случае достаточно исследовать только платежную матрицу игрока  .
.
В данной игре игрок  стремится выбрать такую строку матрицы, чтобы максимизировать свой выигрыш, а игрок
стремится выбрать такую строку матрицы, чтобы максимизировать свой выигрыш, а игрок  – такой столбец матрицы, чтобы минимизировать свой проигрыш.
– такой столбец матрицы, чтобы минимизировать свой проигрыш.
| Bj Ai | B1 | B2 | B3 | … | Bn |
| A1 | α11 | α12 | α13 | … | α1n |
| A2 | α21 | α12 | α13 | … | α2n |
| … | … | … | … | … | … |
| Am | αm1 | αm2 | αm3 | … | αmn |
Рис. 7.1
Пример:
Игра полковника Блотто
Две армии ведут борьбу за два исходных пункта. Армия полковника Блотто (игрок А) состоит из 4–х формирований, армия противника (игрок В) – из 3–х. Правила игры: армия посылает больше формирований, занимает его и уничтожает посланные туда формирования противника. В случае равенства сил противник очков не получает. Общий выигрыш определяется как сумма выигрышей в 2–х пунктах. Платежная матрица представлена на рис. 7.2.
| Bj Ai | 3,0 | 0,3 | 2,1 | 1,2 | |
| 4,0 | |||||
| 0,4 | |||||
| 3,1 | –1 | –1 | |||
| 1,3 | –1 | –1 | |||
| 2,2 | –2 | –2 | –2 | ||
| 3\0 |
Рис. 7.2
Задачей теории игр является нахождение решения игры, т.е. определение для каждого игрока его оптимальной стратегии и цены игры.
Оптимальной называется стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или максимально возможный средний проигрыш) независимо от поведения противника.
Ценой игры называется выигрыш (проигрыш), соответствующий оптимальным стратегиям игроков.
В теории игр наилучшим принято считать поведение игроков, при котором каждый игрок предполагает, что его противник не глупее ( принцип разумности ).
Если игрок А выбрал стратегию i, то его выигрыш составит

Отсюда максимальный гарантированный выигрыш
 .
.
Стратегия, соответствующая  называется максиминной стратегией, а
называется максиминной стратегией, а  – нижней ценой игры или максимином.
– нижней ценой игры или максимином.
Игрок В, рассуждая аналогично, может среди всех своих стратегий выбрать ту, которая обеспечит ему минимальный гарантированный проигрыш.

Стратегия, соответствующая  называется минимаксной стратегией, а величина
называется минимаксной стратегией, а величина  – верхней ценой игры или минимаксом.
– верхней ценой игры или минимаксом.
Если игрок А будет придерживаться максиминной стратегии, то он получает выигрыш не меньше максиминного значения, т.е.

Если игрок В придерживается минимаксной стратегии, то его проигрыш будет не больше минимального значения, т.е.

В общем случае отношения между нижней и верхней ценой игры устанавливаются неравенством

Существуют игры, для которых  . Элемент платежной матрицы, отвечающей этим стратегиям, называется Седловой точкой. Ей отвечает цена игры
. Элемент платежной матрицы, отвечающей этим стратегиям, называется Седловой точкой. Ей отвечает цена игры  :
:

Если  , то игра выгодна игроку А.
, то игра выгодна игроку А.
При  игра выгодна игроку В.
игра выгодна игроку В.
Если  , то игра выгодна обоим игрокам и называется безобидной или справедливой.
, то игра выгодна обоим игрокам и называется безобидной или справедливой.
7.3. Игра 2–х лиц без седловой точки. Смешанные стратегии
Одна из возможностей расширения стратегий игроков – разнообразить способ выбора своей стратегии, например, «случайно».
Как мы уже отмечали, в отсутствии Седловой точки, игрок А, применяя свою максиминную стратегию, выиграет не менее  , а игрок В, применяя свою минимаксную стратегию, проигрывает не более
, а игрок В, применяя свою минимаксную стратегию, проигрывает не более  , где
, где  . Применение чистых стратегий в каждой партии такой игры не дает возможность игрокам увеличить выигрыш
. Применение чистых стратегий в каждой партии такой игры не дает возможность игрокам увеличить выигрыш  , чем уменьшить проигрыш
, чем уменьшить проигрыш  . Для того, чтобы это было возможным необходимо применять не одну, а несколько чистых стратегий, чередуя их случайным образом с какими–то частотами. Такая стратегия получила название смешанной (ее элементами являются чистые стратегии).
. Для того, чтобы это было возможным необходимо применять не одну, а несколько чистых стратегий, чередуя их случайным образом с какими–то частотами. Такая стратегия получила название смешанной (ее элементами являются чистые стратегии).
Смешанная стратегия имеет смысл при условии, что игра состоит более чем из одной партии.
Обозначим смешанные стратегии игроков А и В через
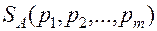 и
и 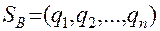 , где
, где
 – вероятность (частота) применения игроком А чистой стратегии
– вероятность (частота) применения игроком А чистой стратегии  ,
,  – вероятность (частота) принятия игроком В чистой стратегии
– вероятность (частота) принятия игроком В чистой стратегии  .
.
Причем 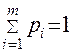 и
и  .
.
Чистые стратегии игроков А и В, для которых вероятности  и
и  отличны от 0, называются активными.
отличны от 0, называются активными.
Теорема (основная теорема теории игр) (теорема минимакса).
Любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение (т.е. пару оптимальных стратегий, в общем случае смешанных) и соответствующую цену.

Решение игры, не имеющей Седловой точки, может осуществляться различными методами. Рассмотрим наиболее важные из них.
7.3.1. Графическое решение игр вида (2×n) и (m×2)
Этот метод применим только к играм, в которых хотя бы один игрок имеет только две стратегии.
Рассмотрим следующую игру (без Седловой точки)

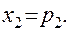

Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, представлены в таблице
| В А | 
| 
| … | 
|

| 
| 
| … | 
|

| 
| 
| … | 
|
Отсюда видно, что ожидаемый выигрыш игрока А линейно зависит от  . В соответствии с критерием минимакса игрок А должен выбирать
. В соответствии с критерием минимакса игрок А должен выбирать  так:
так:
| Чистые стратегии игрока В | Ожидаемые выигрыши игрока А |

| |

| |
| … | … |
| N | 
|
Пример:
| Вj Аi | В1 | В2 | В3 |
| ||
| А1 |   6 6
| |||||
| А2 | ||||||
| А3 | ||||||
| А4 |
Замечания: Стратегии, для которых есть доминирующие и дублирующие стратегии можно отбрасывать.
| Вj Аi | В1 | В2 | В3 | В4 |
| А1 | ||||
| А4 |
|

| Вj Аi | В1 | В2 | В4 | |
| А1 | ||||
| А4 | ||||

| Чистая стратегия Игрок В | Ожидаемый выигрыш игрока А | 
 – цена игры – цена игры

| ||
| –6х1 + 8 | ||||
| –2х1 + 6 | ||||
| 5х1 + 1 | ||||
| Чистая стратегия Игрока А | Ожидаемый выигрыш Игрока В | 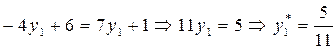

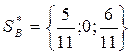
| |
| –4у1+6 | |||
| 7у1+1 | |||
 |
7.3.2. Решение игр “m×n” симплекс–методом
Допустим, что все элементы платежной матрицы  положительны. Этого можно добиться, добавив ко всем членам матрицы достаточно большое число М. Это приведет к увеличению цены игры
положительны. Этого можно добиться, добавив ко всем членам матрицы достаточно большое число М. Это приведет к увеличению цены игры  на М, а оптимальное решение
на М, а оптимальное решение 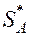 и
и 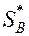 не изменится.
не изменится.
| B A | q1 | q2 | … | qn |
| p1 | α11 | α12 | … | α1n |
| p2 | α21 | α12 | … | α2n |
| … | … | … | … | … |
| pm | αm1 | αm2 | … | αmn |
Найдем сначала 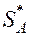 . На основе принципа целесообразности.
. На основе принципа целесообразности.
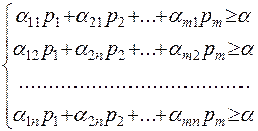 или
или

где 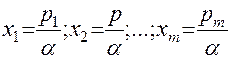
Очевидно: 
Таким образом, решение игры свелось к следующей задаче
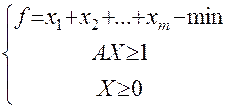 (1) – это задача линейного программирования
(1) – это задача линейного программирования
Оптимальная стратегия игрока В находится аналогично. Она является решением задачи.


 (2)
(2)


Нетрудно видеть, что задачи (1) и (2) – пара двойственных задач. Следовательно,  .
.
Date: 2016-02-19; view: 1014; Нарушение авторских прав