Понятие множества

Что такое множество? Ответить на этот вопрос не так просто, как это кажется на первый взгляд. В повседневной жизни и практической деятельности часто приходится говорить о некоторых совокупностях различных объектов: предметов, понятий, чисел, символов и т. п. Например, совокупность деталей механизма, аксиом геометрии, чисел натурального ряда, букв русского алфавита. На основе интуитивных представлений о подобных совокупностях сформировалось математическое понятие множества как объединения отдельных объектов в единое целое. Именно такой точки зрения придерживался основатель теории множеств немецкий математик Георг Кантор.

Множество относится к категории наиболее общих, основополагающих понятий математики. Поэтому вместо строгого определения обычно принимается некоторое основное положение о множестве и его элементах. Так, группа выдающихся математиков, выступающая под псевдонимом Н. Бурбаки, исходит из следующего положения: «Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или с элементами других множеств».

2. Множество и его элементы. Утверждение, что множество А состоит из различимых элементов 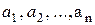(и только из этих элементов), условно записывается 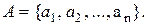Принадлежность элемента множеству (отношение принадлежности) обозначается символом , т. е. a₁ А, a₂ А, …, a_n А, или короче 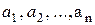A. Если b не является элементом A, то пишут b A или b A.

Два множества А и В равны (тождественны), А = В, тогда и только тогда, когда каждый элемент А является элементом В и обратно. Это значит, что множество однозначно определяется своими элементами.

Множество может содержать любое число элементов — конечное или бесконечное. Соответственно имеем конечные (множество цифр О, 1,..., 9 или страниц в книге) или бесконечные (множество натуральных чисел или окружностей на плоскости) множества. Не следует, однако, связывать математическое понятие «множество» с обыденным представлением о множестве как о большом количестве. Так, единичное (одноэлементное) множество содержит только один элемент. Более того, вводится также понятие пустого множества, которое не содержит никаких элементов. Пустое множество обозначается специальным символом Ø.

Роль пустого множества Ø аналогична роли числа нуль. Это понятие можно использовать для определения заведомо несуществующей совокупности элементов (например, множество зеленых слонов, действительных корней уравнения х²+1=0). Более существенным мотивом введения пустого множества является то, что заранее не всегда известно (или неизвестно вовсе), существуют ли элементы, определяющие какое-то множество. Например, множество выигрышей в следующем тираже спортлото на купленные билеты может оказаться пустым. Никто еще не знает, является ли пустым или нет множество всех решений в целых числах уравнения х³ + у³ + z³ == 30. Без понятия пустого множества во всех подобных случаях, говоря о каком-нибудь множестве, приходилось бы
добавлять оговорку «если оно существует».

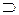Множество и подмножества. Множество A, все элементы которого принадлежат и множеству В, называется подмножеством (частью) множества В. Это отношение между множествами называют включением и обозначают символом , т. е. А В (А включено в В) или В А (В включает А). Например, множество конденсаторов электронной цепи является подмножеством всех ее компонентов, множество положительных чисел — это подмножество множества действительных чисел.

Отношение A В допускает и тождественность (A=В), т. е. любое множество можно рассматривать как подмножество самого себя (A A). Полагают также, что подмножеством любого множества является пустое множество Ø, т. е. Ø А. Одновременное выполнение соотношения A В и B A возможно только при A=В. И обратно A=В, если A В и B А. Это может служить определением равенства двух множеств через отношение включения.

Наряду с A В, в литературе можно встретить и другое обозначение A 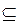В. При этом под A В понимают такое отношение включения, которое не допускает равенства

A и В (строгое включение). Если допускается А=В, то пишут A 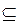В (нестрогое включение). Мы будем придерживаться принятого ранее обозначения как для строгого, так и для нестрогого включения.

Множество подмножеств. Любое непустое множество А имеет, по крайней мере, два различных подмножества: само А и пустое множество Ø. Эти подмножества называются несобственными, а все другие подмножества А называют собственными (эта терминология связана со словами «собственно подмножества», а не со словом «собственность»). Конечные собственные подмножества образуются всевозможными сочетаниями по одному, два, три и т. д. элементов данного множества.

Элементы множества сами могут являться некоторыми множествами. Например, книга из множества книг в шкафу может рассматриваться как множество страниц. Здесь следует обратить внимание на то, что речь идет об элементах множества, а не о подмножествах (никакая совокупность страниц не может рассматриваться как подмножество множества книг).

Множество, элементами которого являются все подмножества множества А, называют множеством подмножеств (множеством-степенью) А и обозначают через Р (А). Так, для трехэлементного множества А={а, Ь, с} имеем Р (А)={ Ø, {а}, {b}, {c}, {а,b}, {а,c},{c,b},{а,b,c}}.

В случае конечного множества A, состоящего из n элементов, множество подмножеств Р (А) содержит элементов. Доказательство основывается на сумме всех коэффициентов разложения бинома Ньютона или на представлении подмножеств n-раз- рядными двоичными числами, в которых 1 (или 0) соответствует элементам подмножеств.

Следует подчеркнуть различия между отношением принадлежности и отношением включения. Как уже указывалось, множество A может быть своим подмножеством (A A), но оно не может входить в состав своих элементов (A A). Даже в случае одноэлементных подмножеств следует различать множество A={a} и его единственный элемент а. Отношение включения обладает свойством транзитивности: если A B и B C, то A C. Отношение принадлежности этим свойством не обладает. Например, множество A={1, {2,3},4} в числе своих элементов содержит множество {2, 3}, поэтому можно записать: 2,3 {2, 3} и {2, 3} A. Но из этого вовсе не следует, что элементы 2 и 3 содержатся в A (в приведенном примере мы не находим 2 и 3 среди элементов множества A, т. е. 2, 3 A.

Date: 2016-02-19; view: 676; Нарушение авторских прав