Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Порядок выполнения работы. Цель работы: исследование временного и спектрального представления сигналов: гармонического сигнала

Тема. ИССЛЕДОВАНИЕ СИГНАЛОВ И ИХ СПЕКТРОВ

Цель работы: исследование временного и спектрального представления сигналов: гармонического сигнала, сложного сигнала, сложного сигнала на фоне шума, узкополосного сигнала, последовательности прямоугольных импульсов.

Таблица 1.1Варианты задания на лабораторную работу

Параметр № варианта
                   
Частота модулирующего сигнала f M, Гц 0,5                  
Амплитуда модулирующего сигнала А М, В   1,5 0,5   2,5       0,5  
Скважность двоичных импульсов S 1,5           1,5      
Частота несущей F Н, Гц                    
Индекс АМ mAM 0,5 0,7 0,8 0,9 0,6 0,8 0,9 0,7 0,5 0,6
Индекс ЧМ k ЧМ, Гц/В                    
Индекс ФМ bФМ, рад p p/2 3p/4 2p/3 p 2p/3 p 3p/4 p/2 2p/3

 

Порядок выполнения работы

 

1. Исследование гармонического сигнала.

1.1. Загрузите в среде Матлаб программу f1.m.

1.2. Задайте частоту и амплитуду сигнала согласно заданию (табл.1.1).

1.3. Запустите программу и снимите эпюры и спектры сигналов.

1.4. Измените частоту сигнала умножив ее на коэффициент изменения частоты и повторите измерения.

Таблица 1.1 Варианты задания

Параметр № варианта
                   
Амплитуда A1, В 0,5                  
Частота сигнала F1, Гц                    
Коэффициент изменения частоты   2,5   0,5 0,5 0,5 0,5 0,5 0,25 0,25

 

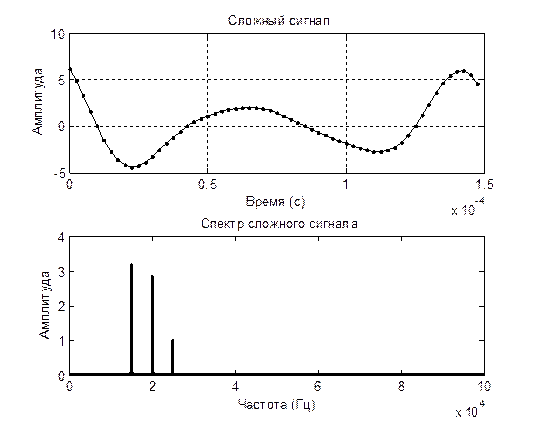
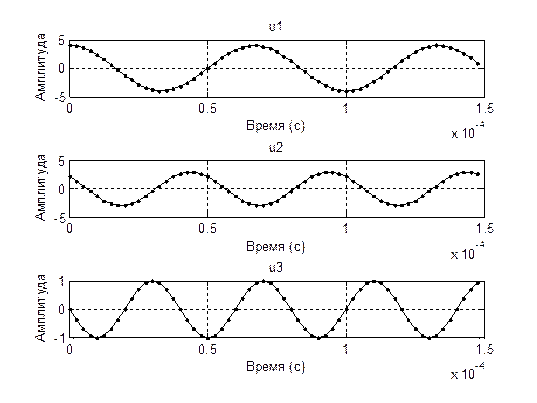
2. Исследование сложного сигнала.

2.1. Загрузите в среде Матлаб программу f2.m..

2.2. Задайте частоты и амплитуды гармонических сигналов согласно варианту задания (табл.1.2)..

Таблица 1.2 Варианты задания

Параметр № варианта
                   
Амплитуда A1, В 0,5                  
Амплитуда A2, В   0.5 0.5              
Амплитуда A2, В   0.25 0.2 0.5            
Частота сигнала F1, кГц                    
Частота сигнала F2, кГц                    
Частота сигнала F3, кГц                    
Коэффициент изменения частоты 2.5   1.5 2.5   1.5 2.5   1.5 0,25

 

2.3. Запустите модель и снимите эпюры и спектры сигналов.

2.4. Измените частоту сигнала умножив ее на коэффициент изменения частоты и повторите измерения.

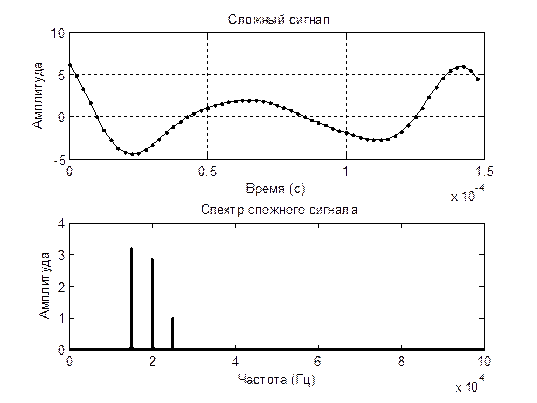
2.5. Установите значение длительности сигнала равным 600 и повторите измерения.

3. 2. Исследование сложного сигнала на фоне шума.

2.1. Загрузите в среде Матлаб программу f3.m..

2.2. Задайте частоты и амплитуды гармонических сигналов согласно варианту задания (табл.1.3)..

 

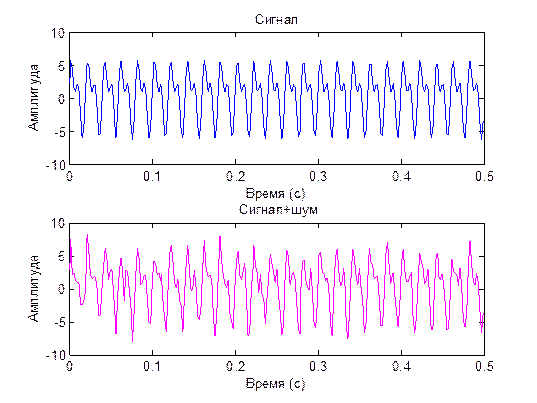
Таблица 1.3 Варианты задания

Параметр № варианта
                   
Амплитуда A1, В 0,7                  
Амплитуда A2, В   0.5 0.5              
Частота сигнала F1, Гц                    
Частота сигнала F2, Гц                    
Дисперсия шума An                    
Коэффициент изменения дисперсии шума 2.5   1.5 2.5   1.5 0.5   0.5  


 

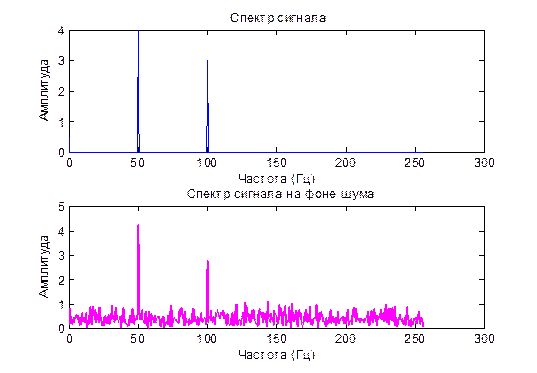
3.3. Запустите модель и снимите эпюры и спектры сигналов.

3.4. Измените дисперсию шума умножив ее на коэффициент изменения частоты и повторите измерения.

 

 

4. Исследование узкополосного сигнала.

4.1. Загрузите в среде Матлаб программу f4.m..

4.2. Задайте частоту и амплитуду сигнала согласно варианту задания (табл.1.4)..

 

 

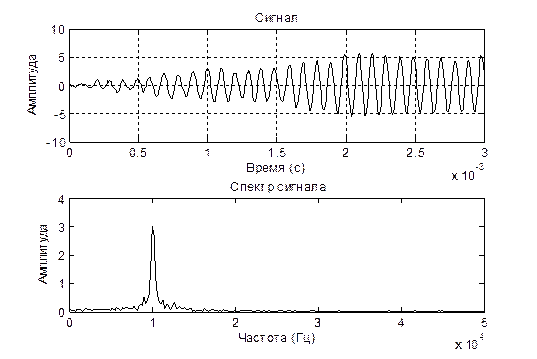
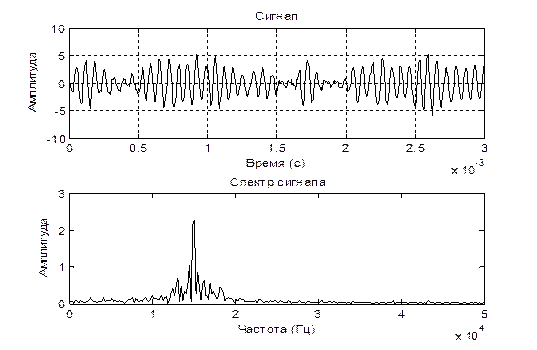
Таблица 1.4 Варианты задания

Параметр № варианта
                   
Амплитуда A1, В                    
Частота сигнала f, кГц                    
Коэффициент изменения частоты 2.5   1.5 0.5 0.5 1.5 1.5   0.6 0,25

4.3. Запустите модель и снимите эпюры и спектры сигналов.

4.4. Измените частоту сигнала умножив ее на коэффициент изменения частоты и повторите измерения.

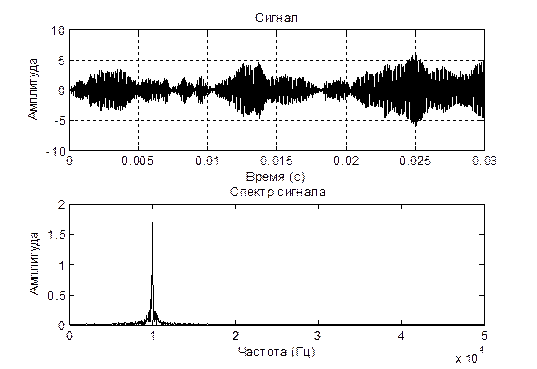
4.5. Установите значение длительности сигнала равным 6000 и повторите измерения.

5. Исследование периодической последовательности прямоугольных импульсов

5.1. Загрузите в среде Матлаб программу f5.m..

5.2. Задайте частоту, амплитуду и скважность импульсов согласно варианту задания (табл.1.5)..

Таблица 1.5 Варианты задания

Параметр № варианта
                   
Амплитуда Um, В 0.5   0.3   2.5 2.6 1.5 1.8 0.9  
Частота сигнала Fs, кГц                    
Скважность                    
Коэффициент изменения скважности     0.5 0.4 0.5         0,5

5.3. Запустите программу и снимите эпюры и спектры сигналов.

5.4. Измените скважность импульсов умножив ее на коэффициент изменения скважности и повторите измерения.

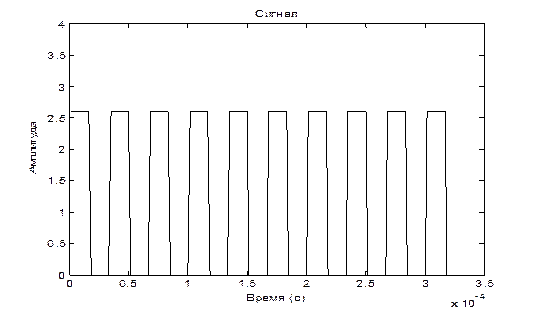
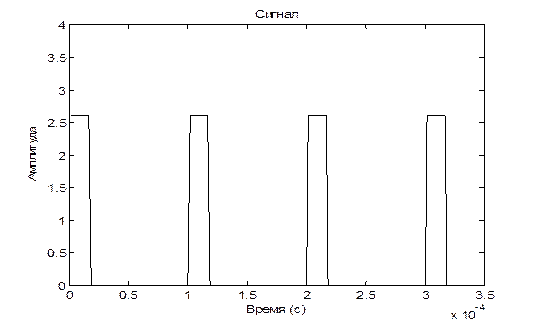
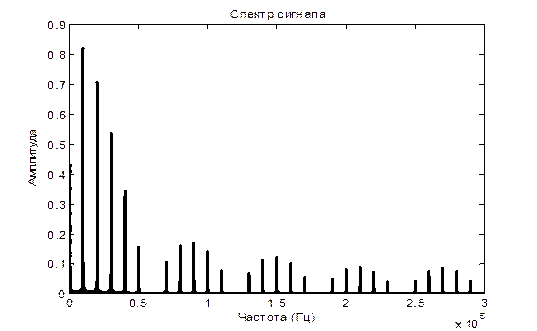
Вывод: в ходе проведенных исследований временного и спектрального пред-ставления сигналов различных форм мы выяснили, что для простого гармони-ческого сигнала характерно такое свойство, что по мере увеличения его частоты увеличивается дисперсия амплитуды сигнала. Данная особенность выполняется и для сложного сигнала, что заметно на построенном графике. Данные искаже-ния еще отчетливее проявляются при наличии шума, в данном случае- низкоам-плитудных шумовых сигналов, распределенных по всей ширине частотного спектра. Для узкополосных сигналов характерно отклонение функции ампли-туды от основного закона нарастания изменения амплитуды вследствие перехо-да в более высокочастотную область спектра. Для периодической последова-тельности прямоугольных импульсов характерно расширение и больший разброс спектра частот пропорционально увеличению скважности. В результате этого сигналы в амплитудно-частотном спектре группируются вокруг определенных значений частоты, где наблюдаются максимумы амплитуды в центральной зоне и её затухание по мере отдаления в обоих направлениях.



<== предыдущая | следующая ==>
Курсовая работа. По дисциплине «экономика организации» | Основной материал: сталь листовая 09Г2С. Подобраны сварочные материалы и сварочное оборудование и обоснован их выбор. Разработана технология сборки и сварки кронштейна





Date: 2016-01-20; view: 835; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.016 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию