Понятие, назначение и преимущества системы СПУ

Объектами сетевого моделирования на производстве являются комплексы работ по подготовке производства изделий, а также изготовлению самих изделий.

Под методом СПУ понимается аппарат построения, расчета, анализа и оптимизации сетевых моделей. Назначение метода – это решение отдельных задач, связанных с планированием производства. Метод СПУ включается в систему СПУ, которая представляет собой постоянно действующий механизм, соединяющий учет и контроль с процедурами выработки и выбора управленческих решений. Такой механизм подвергается регулированию, начиная с составления плана реализации комплекса работ и кончая моментом полного его завершения.

Целью применения системы СПУ выступает разработка оптимального или достаточно близкого к нему варианта плана производства, обеспечивающего рациональную увязку во времени и в пространстве выполняемых работ и наилучшее использование ресурсов, а также эффективное управление процессом реализации этого плана. В результате применения сетевых моделей сокращается продолжительность подготовительных и производственных процессов, снижается их трудоемкость и себестоимость, растет производительность труда.

В основе системы СПУ лежит модель, описывающая объект управления в виде сетевого графика (из чего следует название системы). Сетевой график - это логико-математическая модель, которая отражает технологические и организационные взаимосвязи работ по выполнению комплекса операций. Модель представляет собой стрелочную диаграмму, отображающую последовательность осуществления всех операций, из взаимосвязи и зависимости, отражающие закономерности технологии производства и принятые решения по выполнению программы работ для достижения заданной цели.

Сетевой график по сравнению с ленточным (графики Ганта) обладает рядом преимуществ, таких как:

1. позволяет выявить и отразить все взаимосвязи работ и операций по выполнению поставленной цели;

2. отражает динамику фактического хода работ с учетом изменений условий их выполнения;

3. на графике может быть легко выявлена технологическая последовательность работ, которая определяет конечные сроки всей разработки – критический путь;

4. выделяет наиболее напряженные работы (лежащие на критическом пути), от которых зависит продолжительность производственного цикла или выполнение поставленной цели;

5. позволяет определить резервы времени работ (не лежащие на критическом пути), что позволяет наиболее рационально перераспределять наличные людские, материальные и финансовые ресурсы;

6. создает возможность оптимизации выполнения производственных процессов;

7. обеспечивает условия для расчета его на ЭВМ.

2. Элементы сетевого графика

В основе сетевого графика лежат такие термины, как «работа» и «событие».

Работа – это часть технологического процесса, которая может быть выполнена отдельными производственными подразделениями и требует для своего осуществления затрат времени, труда, ресурсов. Работу на графике изображают стрелкой, длина которой не связана с продолжительностью работы (если график составлен не в масштабе времени). Под стрелкой указывают наименование работы, а над стрелкой – продолжительность работы в рабочих днях и при необходимости в скобках указывают количество рабочих в день (рис. 1).

Продолжительность работы (дней)

Число рабочих в день (человек)

15 (3)

Разработка эскизного проекта

Наименование работы

Рис. 1. Изображение работ и событий

Различают следующие значения термина «работа» (рис.2):

1) действительная работа () – производственный процесс, требующий затрат времени и ресурсов (например, проектирование рабочих чертежей, изготовление деталей и т.д.);

2) ожидание () – процесс, требующий затрат времени, но не требующий затрат ресурсов, являющийся технологическим или организационным перерывом между работами, непосредственно выполняемыми друг за другом (естественные процессы: сушка древесины, охлаждение деталей после термообработки и т.д.);

3) зависимость (фиктивная работа -) – условный элемент, не требующий затрат времени, труда и ресурсов, а вводимый для отражения логической взаимосвязи между двумя смежными работами или процессами.

(Действительная работа) (Ожидание) (Фиктивная работа)

Термообработка деталей Охлаждение деталей

9 (3) 1(0) 0 (0)

Рис.2. Изображение работ

Событие () – факт свершения одной или нескольких работ, без чего невозможно начало последующих. Событие совершается мгновенно и поэтому не нуждается в затратах времени и ресурсов. Изображается в основном в виде кружочка (или иных геометрических фигур), внутри которого указывается определенный номер – код события (например, η, i, j или k на рисунке 3).

Предшествующая Данная Последующая

работа работа работа

Рис. 3. Обозначение работ и событий

Таким образом, события устанавливают технологическую и организационную последовательность работ. Различают следующие события (рис. 4; 5):

1. начальное событие – определяет начало данной работы и является конечным для предшествующих работ;

2. конечное событие – определяет окончание данной работы и является начальным для последующих работ;

3. исходное событие – событие, которое не имеет предшествующих работ;

4. завершающее событие – событие, которое не имеет последующих работ;

5. сложное событие – событие, в которое входят или из которого выходят две или более работы.

Начальное Начальное Начальное Завершающее

событие событие событие событие

работы 1-2 работы 2-3 работы 3-4 сети

Исходное Конечное Конечное Конечное

событие событие событие событие

сети работы 1-2 работы 2-3 работы 3-4

Рис.4. Изображение событий и работ

Рис. 5. Изображение сложных событий

Между исходным и завершающим событием лежит несколько технологически связанных между собой цепочек работ, выполняемых последовательно. Поскольку к некоторым событиям примыкают «входящие» и «выходящие» работы, выполняемые параллельно, цепочки последовательно выполняемых работ как бы пересекаются, образуя сеть с узлами в местах событий.

Так как каждая работа в сетевом графике имеет продолжительность ее выполнения, то, пройдя от исходного события к завершающему событию по каждой цепочке последовательно выполняемых работ, можно подсчитать общую продолжительность работ в каждой цепочке. При этом самый продолжительный по времени путь от исходного события к завершающему называется критическим. Он определяет продолжительность выполнения всей программы работ. На графике критический путь обозначается двойными или жирными стрелками (рис.).

Близкие к критическому по продолжительности пути называются подкритическими. Все другие, менее продолжительные пути называются некритическими, и работы, лежащие на этих путях, - некритическим. Иногда на графике может быть несколько критических путей.

3. Построение сетевого графика

Построение сетевого графика осуществляется в соответствии со следующими требованиями (рис. 6).

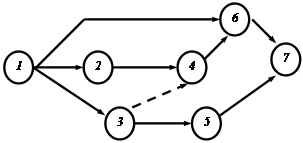
1. График должен быть простым, без лишних пересечений (рис. 6.1).

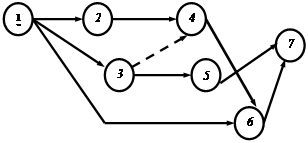неправильно правильно

Рис. 6.1. Требования к построению сетевого графика

2. Стрелки (работы) должны быть направлены слева направо.

3. Между двумя событиями может быть изображена только одна работа.

4. На графике не должно быть замкнутых контуров (рис.6.2).

неправильно правильно

Рис. 6.2. Требования к построению сетевого графика

5. Нумерация (кодирование) событий должна соответствовать последовательности работ во времени, то есть предшествующим событиям присваиваются меньшие номера. Исходному событию присваивается первый номер. Кодирование может вестись вертикальным (рис. 6.3 а)) и горизонтальным (рис. 6.3 б)) способами.

а) б)

Рис. 6.3. Требования к построению сетевого графика

4. Расчет сетевого графика

Расчет сетевого графика заключается в определении его временных (в большинстве случаях), ресурсных и стоимостных параметров. Расчетные параметры включают:

1. i – j – код данной работы;

2. i – код начального события данной работы;

3. j – код конечного события данной работы;

4. h – i – код работ, предшествующих данной работе;

5. h – код событий, предшествующих начальному событию данной работы;

6. j – k – код работ, последующих за конечным событием данной работы;

7. k – код событий, последующих за конечным событием данной работы;

8. продолжительность работы t_i-j;

9. РН _i-j -раннее начало работы i – j – это самый ранний из возможных сроков начала работы с учетом выполнения предшествующих работ;

10. РО _i-j - раннее окончание работы i – j – это срок окончания работы при условии ее начала в самый ранний из возможных сроков;

11. ПН _i-j - позднее начало работы i – j – это самый поздний срок, при котором может быть начата работа без нарушения продолжительности критического пути;

12. ПО _i-j - позднее окончание работы i – j – это предельно допустимый срок, в который может быть окончена работа без нарушения продолжительности критического пути;

13. R_i-j - общий резерв, который показывает интервал времени, в пределах которого может быть увеличена длительность выполнения работы или сдвинуты ее сроки без изменения продолжительности выполнения работ;

14. r_i-j - частный резерв - это часть общего резерва времени, когда может быть увеличена продолжительность или задержаны сроки начала данной работы без изменения общих резервов времени любой последующей работы;

15. t_крит. - продолжительность критического пути – это самый продолжительный по времени путь от исходного до завершающего события, по которому определяется продолжительность всех работ.

Параметры сетевого графика рассчитываются одним из способов: аналитическим, табличным, методом расчета на самом графике, с применением ЭВМ и др.

Наиболее широко применяют метод расчета сетевого графика на самом графике и табличный метод, в которых полностью используются формулы аналитического метода.

Сначала рассчитываются ранние сроки. Для любой сетевой модели раннее начало начального события РН_h-i =0. Раннее окончание РО_h-i =РН_h-i + t_h-i.

Раннее начало РН_i-j принимается равным раннему окончанию РО_h-i. Если к i - му событию подходит несколько работ (стрелок), то для определения РН_i-j выбирается максимальное из всех возможных значений, образующихся в i-м событии, то есть РН_i-j = max PО_h-i. Таким же образом рассчитываем до завершающего события.

Поздние сроки определяются от конечного события к начальному, при этом позднее окончание завершающего события принимается равным раннему окончанию завершающего события (ПО_j-k = max РO_j-k). Позднее окончание работы ПО_i-j = min ПН_j-k. Позднее начало ПН_i-j = ПО_i-j - t_i-j.

Пример 1.

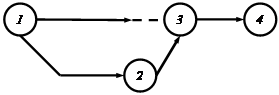5 3

Рис. 7. Базовый сетевой график для расчета

Решение:

Расчет ранних сроков (рис. 7.1).

РО₁₃ = 0 + 5 = 5

РО₂₃ = 9 + 2 = 11

РН₁₂ = 0 РН₃₄ = max PO_nj.= 11

5 3

РН₁₃ = 0 2 РО₃₄ = 11 + 3 = 14

РО₁₂ = 0 + 9 = 9

РН₂₃ = РО₁₂ = 9

Рис. 7.1. Пример расчета ранних сроков

Расчет поздних сроков (рис. 7.2).

ПН₃₄ = 14 – 3 =11

ПН₁₃ = 11 - 5 = 6 ПО₁₃ = 11

ПН₁₂ = 9 – 9 = 0 ПО₂₃ = 11

5 3

2 ПО₃₄ = 14

ПН₂₃ = 11 – 2 =9

ПО₁₂ = 9

Рис. 7.2. Пример расчета поздних сроков

Сетевой график рассчитан правильно, если хотя бы одно из начал исходного события окажется равным 0.

Для анализа сетевых моделей используют понятие резервов времени: общих и частных.

Общий резерв данной работы (R) определяется как разница между поздним началом (ПН) данной работы и раннего начала (РН) данной работы, то есть R_ij = ПО_ij - РО_ij.

В рассматриваемом примере общие резервы имеют следующие значения:

R₁₂ = ПО₁₂ - РО₁₂.= 9 – 9 = 0

R₁₃ = ПО₁₃ - РО₁₃.= 11 – 5 = 6

R₂₃ = ПО₂₃- РО₂₃.= 11 – 11 = 0

R₃₄ = ПО₃₄ – РО₃₄.= 14 – 14 = 0

Общие резервы свидетельствуют, что можно увеличить продолжительность работы 1-3, но не более чем на 6 дней. Полное использование общего резерва R₁₃ = 6 приведет к появлению еще одного критического пути. Наличие нескольких критических путей не желательно в связи с тем, что появляется большое количество работ, которое необходимо контролировать для четкого соблюдения графика.

Частный резерв времени показывает на сколько можно сдвинуть или замедлить (снять на время какие-то ресурсы) выполнение данной работы не изменяя начала последующей работы. Частный резерв (r_ij) равен разности между ранним началом (РН) последующей работы и ранним окончанием (РО) данной работы, то есть r_ij = РН_jk – PO_ij.

1₁₂ = РН₂₃ – PO₁₂.= 9 – 9 = 0

r₁₃ = РН₃₄ – PO₁₃.= 11 – 5 = 6

r₂₃ = РН₃₄ – PO₂₃.= 11- 11 = 0

r₃₄ = РН_4k – PO₃₄.= 14 – 14 = 0

На основании аналитического расчета сетевой модели можно вывести свойства критического пути:

1. критический путь – это самый длительный из всех возможных путей от начального события к конечному;

2. на критическом пути совпадают значения поздних и ранних начал, поздних и ранних окончаний;

3. все резервы на критическом пути равны 0.

Исходя из приведенных выше свойств на графике находят критический путь.

t_крит. = t₁₂ + t₂₃ + t₃₄ = 9 + 2 + 3 = 14

5 3

2

9

- критический путь

Рис. 7.3. Пример определения критического пути

Различают следующие способы расчета сетей на графиках:

1) секторный;

2) дроби;

3) потенциалов;

4) табличный.

4.1 Секторный способ

Суть способа в том, что каждое событие на сетевом графике вычерчивается в увеличенном размере и делится на 4 сегмента (рис.8):

номер события

раннее начало позднее начала

дата привязки к календарю

Рис. 8. Обозначение события при секторном способе расчета сетевого графика

Общий и частный резервы определяются следующим образом:

1. общий резерв данной работы равен разнице правого сектора события, куда данная работа входит, левого сектора, откуда данная работа выходит и характеристики самой работы:

R_ij = ПС - ЛС - t_ij

2. частный резерв равен разнице левого сектора события, куда данная работа входит, левого сектора события, откуда данная работа выходит и временной характеристики самой работы:

r_ij = ЛС – ЛС - t_ij

Привязка к календарю осуществляется по ранним началам с использованием календаря. При этом исключаются выходные и праздничные дни.

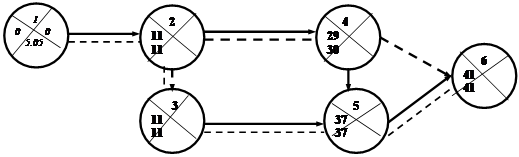
Пример 2.

R₂₄ = 30 –11 - 18 = 1

r₂₄ = 29 - 11 – 18 = 0

11 18 R₄₆ = 41 – 29 – 0 = 12

r₄₆ = 41 - 29 - 0 = 12

R₁₂ = 11 – 0 - 11 = 0

r₁₂ = 11 – 0 -11 = 0 R₂₃ = 11 – 11 – 0 = 0

r₂₃ = 11 – 11 - 0 = 0 4

1 – 11 26

R₅₆ = 41 – 37 – 4 = 0

r₅₆ = 41 - 37 – 4 = 0

R₃₅ = 37 – 11 – 26 = 0

r₃₅ = 37 - 11 – 26 = 0

t_крит. = t₁₂ + t₂₃ + t₃₅ + t₅₆ = 11 + 0 +26 + 4 = 41

Рис. 9. Пример расчета сетевого графика секторным способом

Таким образом, продолжительность всех работ в данном примере составляет 41 день. Первая работа начинается 5 мая, а последняя заканчивается 2 июля.

Секторный способ расчета сетевой модели обладает таким достоинством, как простота алгоритма, недостатком способа является то, что вычерчивание событий в увеличительном размере приводит к увеличению масштаба, а следовательно размеров графика. t₂₄ +

4.2 Способ дроби

Суть метода дроби в том, что сетевая модель выполняется в обычном чертежном варианте, а затем рядом с каждым событием ранние и поздние сроки записываются в виде дроби:

РАННИЕ СРОКИ

ПОЗДНИЕ СРОКИ

Общий и частный резервы определяются следующим образом:

1. общий резерв данной работы равен разнице знаменателя события, куда данная работа входит, числителя события, откуда данная работа выходит и характеристики самой работы:

R_ij = Знам. – Числ. - t_ij

2. частный резерв равен разнице числителя события, куда данная работа входит, числителя события, откуда данная работа выходит и временной характеристики самой работы:

r_ij = Числ. – Числ. - t_ij

Рассмотрим на примере применения данного способа (рис. 10)

Пример 3.

R₁₂ = 7– 0 - 7 = 0 7 R₂₄ = 16 – 7 - 9 = 0 16

0 r₁₂ = 7– 0 -7 = 0 7 r₂₄ = 16 - 7 – 9 = 0 16

0 R₄₆ = 36 – 16 – 20 = 0

7 9 20 r₄₆ = 36 - 16 - 20 = 0

R₁₃ = 16 – 0 – 12 = 4 36

12 r₁₃ = 12 – 0 - 12 = 0 R₃₄ = 16 – 12 – 0 =4 36

r₃₄ = 16 – 12 - 0 = 4 2 R₅₆ = 36 – 29 – 2 = 5

17 r₅₆ = 36 - 29 – 2 = 5

12 29

16 R₃₅ = 34 – 12 – 17 = 5 34

r₃₅ = 29 - 12 – 17 = 0

t_крит. = t₁₂ + t₂₄ + t₄₆ = 7 + 9 +20 = 36

Рис. 10. Пример расчета сетевого графика методом дроби

Date: 2016-01-20; view: 726; Нарушение авторских прав