Погрешности измерения

В результате измерений значение измеряемой величины никогда не может быть определено абсолютно точно. Всегда результат измерения отличается от истинного значения измеряемой величины х на некоторую величину D, называемую погрешностью измерения.

Возникновение погрешностей связано с несовершенством методов и средств измерений, влиянием условий измерений и неправильных действий людей, выполняющих измерения. Конкретная причина той или иной погрешности далеко не всегда может быть установлена.

По характеру проявления погрешности можно подразделить на грубые, систематические и случайные.

Грубые погрешности (промахи, выпадающие точки) появляются из-за неисправности средств измерений, сбоев в их работе, отклонений в режиме работы экспериментальных объектов и т.д. Эти погрешности необходимо обнаружить и искаженные ими результаты исключить из рассмотрения.

Систематические погрешности характеризуются тем, что они или сохраняются постоянными, или изменяются по времени закономерным образом, или являются функциями определенных параметров (температуры, напряжения питания и т.д.).

Систематические погрешности можно подразделить на ряд групп в зависимости от вызывающих их причин.

Погрешности метода, или теоретические погрешности, обусловлены недостаточной разработкой теории измерений, недостаточной обоснованностью принимаемых при этом допущений, неправильным использованием средств измерений, влиянием их на работу экспериментального объекта и т.д.

Инструментальные погрешности возникают из-за недостатков конструкции (схемы) средств измерений или технологии их изготовления.

Дополнительные погрешности (погрешности внешних влияний) вызываются отличием рабочих условий эксплуатации средств измерений от номинальных (неправильная установка; влияние температуры или внешних магнитных и других полей; нестабильность источника питания и т.д.).

Динамические погрешности обусловлены инерционными свойствами средств измерений.

Личные погрешности связаны с индивидуальными особенностями и квалификацией наблюдателя. Личные погрешности исключаются при применении автоматизированных средств измерений с фиксацией результатов измерений на различных носителях информации.

В научно поставленном эксперименте систематические погрешности можно практически полностью исключить или по крайней мере существенно уменьшить путем строгого контроля условий работы при измерениях (термостатирование, экранирование, защита от вибраций, применение стабилизированных источников питания), градуировки и внесения поправок, надлежащей организации измерений и их обработки.

Результат измерения, содержащий систематическую погрешность q, называется неисправленным х' в отличие от исправленного результата х, систематическая погрешность из которого исключена путем введения поправки q: х=х'+q. Поправка равна систематической погрешности и обратна ей по знаку: q=-q.

Поправки могут определяться при градуировке средств измерений, когда измеряемая величина воспроизводится образцовой мерой и ее значение известно, или в результате расчета на основе специальных исследований физических процессов, сопутствующих измерениям.

Случайные погрешности вызываются неконтролируемыми изменениями условий измерений и параметров средств измерений. Если в опытах отсутствует систематическая погрешность, то данные большого числа отдельных измерений (наблюдений) будут случайным образом изменяться в некотором интервале около истинного значения измеряемой величины. Поскольку поправки на систематические погрешности определяются с ограниченной точностью, то они содержат и некоторую случайную погрешность, исключить которую невозможно. Эта погрешность называется неисключенным остатком систематической погрешности.

Таким образом, суммарная случайная погрешность состоит из собственно случайной погрешности и не исключенного остатка систематической погрешности,

Случайная погрешность представляет собой непрерывную случайную величину, т.е. такую величину, которая может принимать в зависимости от случайного исхода наблюдения (опыта) любые значения с определенными вероятностями. Случайная величина наиболее полно характеризуется интегральной F(x) или дифференциальной р(х) функциями распределения. Последняя называется также плотностью вероятностей, или законом (функцией) распределения. Значение функции F(x) при некотором заданном значении х равно вероятности того, что случайная величина x примет значение, меньшее или равное х: F(x)=Р(x£x). Плотность вероятностей есть производная функции F(x): р(х)=F'(x). Обратная зависимость имеет вид . Характерный вид графиков функций F(x) и р(х) представлен на рис. 2.1. График функции р(х) называется также кривой распределения.

Рис. 2.1. Характерный вид графиков интегральной (а) и дифференциальной (б) функций распределения (заштрихована площадь, равная g=Р(х₁£х£х₂)

На практике удобнее пользоваться не функциями распределения, а некоторыми числовыми характеристиками, дающими достаточные сведения о свойствах и распределении случайной величины. Наиболее важными из них являются математическое ожидание М[х] и дисперсия s²[х].

Математическое ожидание характеризует расположение центра распределения, вокруг которого группируются возможные значения случайной величины. Оно определяется интегралом .

Дисперсия s²[х] характеризует рассеяние случайной величины вокруг ее математического ожидания. Дисперсией называется математическое ожидание (т.е. среднее значение) квадрата отклонения случайной величины от М[х]:

Корень квадратный да дисперсии - величина s[х] - имеет ту же размерность, что и сама случайная величина, и называется средним квадратическим отклонением случайной величины.

Конкретные значения указанных характеристик случайных величин зависят от вида функции распределения.

В теории вероятностей, математической статистике, метрологии важную роль играет так называемое нормальное, или Гауссово распределение случайной величин. Плотность вероятностей этого распределения описывается функцией

В теории вероятностей доказано (центральная предельная теорема), что если некоторая случайная величина является суммой большого числа других взаимно независимых случайных величин, ни одна из которых не обладает дисперсией, значительно превосходящей остальные, то независимо от законов распределения слагаемых суммарная величина имеет нормальное распределение.

Если ввести переменную , то получится нормированное нормальное распределение с математическим ожиданием, равным нулю, и дисперсией, равной единице:

Это универсальное, независящее от а и s(х) распределение. Наряду с функцией j(z), применяется в вычислениях также интегральная функция . Эти функции затабулированы в виде таблиц или в виде стандартных программ для ЭВМ.

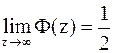Функция j(z) является четной, симметричной относительно оси z=0 и . В силу этого Ф(-z)=-Ф(z); . Между функциями распределения р(х), F(x) и затабулированными (стандартными) функциями j (z) и Ф(z) существует простая связь:

.

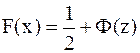Государственным стандартом предписывается ряд способов выражения точности измерений с использованием рассмотренных выше характеристик случайных величин. На практике чаше всего применяется интервальный способ, т.е. точность измерений выражается интервалом (доверительный интервал), в котором с заданной вероятностью у (доверительная вероятность) находится суммарная погрешность измерения. Запись результата измерения величины А с нижней D_н и верхней D_в границами погрешности D при установленной вероятности g имеет следующий вид: А; D от D_н до D_в; g. Например, 450 К; D от 2 К до 4 К; g=0,95.

Доверительным является интервал (х₁=А- D_н; х₂=А+D_в), т.е. (448 К; 454 К).

Рис. 2.2. Графики зависимостей от величин вероятности от нормированных критических значений случайной величины для нормального распределения (f=¥) и распределение Стьюдента (f¹¥)

Для нормального распределения значение доверительной вероятности в общем случае находится по формуле g=Р(z₁<z<z₂)=Ф(z₂)-Ф(z₁). Если |z₁|=|z₂|=|z|, то g=Р(|z|£z_g)=2Ф(z_g). Значения z_g называются квантилями, или критическими значениями для данной вероятности g. На рис. 2.2 приведены значения g в зависимости от z_g (кривая n=¥). Так, при z_g=±1 значение g=0,68, т.е. вероятность погрешностей, не превышающих по абсолютной величины одну среднюю квадратическую погрешность, составляет 0,68. При z_g=±2 величина g равна уже 0,95, а при z_g=±3 g=0,997. В последнем случае только 0,3 % всех случайных погрешностей выходит за пределы трех средних квадратических погрешностей. Доверительная граница случайной погрешности D(А)=|x-А|= z_gs(х).

Доверительная вероятность задается в соответствии со смыслом задачи и практическим значением риска ошибки, который неизбежно появляется, когда весь принципиально возможный диапазон изменения случайной величины ограничивается некоторыми, заведомо более узкими, доверительными пределами.

В 6ольшинстве практических задач принято ограничиваться значением g=0,95, т.е. считается допустимым, что 5 % результатов наблюдений (одна точка из двадцати) могут выйти за установленные пределы.

Однако в особо ответственных случаях, связанных, например, с определением основных характеристик двигателя, с его надежностью, прочностью, безотказностью, где ошибочная трактовка результата может привести к серьезным последствиям, необходимо выбирать более высокую доверительную вероятность.

Если погрешность D выражена в единицах измеряемой величины, то она называется абсолютной. На практике чаще оперируют с относительной погрешностью измерений, которая представляет собой отношение абсолютной погрешности к результату измерения d= D/x_изм. Значение d часто выражается в процентах.

Для характеристики точности средств измерения применяется приведенная погрешность - отношение абсолютной погрешности к некоторому нормирующему значению x_N, характерному для данного вида средств измерений. Например, значение х_N принимается равным большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерений, и сумме модулей пределов измерений, если нулевая отметка расположена внутри диапазона измерений и др.

Для ряда средств измерений устанавливается класс точности, являющейся обобщенной характеристикой средства измерений, определяемой пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность.

Под пределом допускаемой основной погрешности понимается наибольшая (по модулю) погрешность средства измерения, при которой оно может быть признано годным при эксплуатации в стандартных условиях. Например, достаточно распространенным является установление пределов допускаемой приведенной основной погрешности по формуле g_д= D_д^.100/x_N=±р, где D_д - пределы допускаемой абсолютной погрешности; x_N - нормирующее значение; р - положительное число (в процентах), равное классу точности и выбираемое из следующего ряда: 1^.10ⁿ 1,5^.10ⁿ; 2^.10ⁿ; 2,5^.10ⁿ; 4^.10ⁿ; 5^.10ⁿ; 6^.10ⁿ (n=1; 0; -1; -2 и т.д.). По классу точности всегда можно установить пределы допускаемой погрешности.

С классом точности связаны также пределы дополнительных погрешностей и другие характеристики средств измерений, влияющие на точность измерений. Эти характеристики нормируются частными стандартами на отдельные виды средств измерений.

В качестве показателей, характеризующих динамические свойства средств измерений, нормируются наиболее часто полоса пропускаемых частот сигнала и время установления выходной величины.

Date: 2016-01-20; view: 641; Нарушение авторских прав