Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод относительных погрешностей
|
|
В некоторых случаях функция преобразования измерительного устройства выражается произведением нескольких множителей и является постоянной величиной, не зависящей от изменения входной величины. Для таких случаев может быть применён метод относительных погрешностей. Механизмы, состоящие из рычагов или фрикционных передач, нередко исследуют и рассчитывают, используя понятие об относительной погрешности. Различают два вида относительных погрешностей: радиальная погрешность и тангенциальная погрешность.
Относительной радиальной погрешностью называют частное от деления абсолютного отклонения радиального размера на номинальное значение этого размера.
Для относительной радиальной погрешности характерно то обстоятельство, что в последовательной передаче, в независимости от принадлежности отклонения к любому звену, погрешность имеет постоянный коэффициент влияния ±1.
Выходные параметры многих преобразовательных элементов измерительных устройств выражаются сложной степенной зависимостью через величины его отдельных параметров: пружины, мембранные коробки, сильфоны, индуктивные преобразователи и т.д.
Выходной сигнал: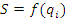 
.
Относительная ошибка: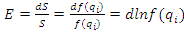 
, т.е. относительная ошибка функции равна дифференциалу натурального логарифма этой функции. Аналогично, что если функция зависит от нескольких параметров, то максимальное значение относительной ошибки результата равно полному дифференциалу натурального логарифма функции, причём при вычислении дифференциала следует брать сумму абсолютных значений дифференциалов всех членов логарифма (т.е. все частные ошибки складываются).
Пример: расчёт усилия винтовых цилиндрических пружин производится по формуле:
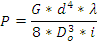
P- осевое усилие пружины.
G- модуль сдвига материала.
d- диаметр проволоки.
λ- ход пружины.
Do-средний диаметр, D- наружный диаметр пружины.
i – число рабочих витков пружины.
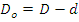
Находим натуральный логарифм P:
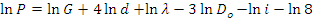
Находим дифференциал этого выражения: причём в правой части берём сумму абсолютных значений его членов
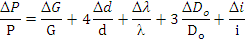
Учитывая вероятностный характер проявления первичных погрешностей, суммарную относительную погрешность осевого усилия пружины находят квадратическим сложением членов приведенного выражения:
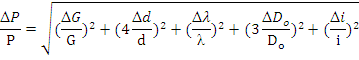
Date: 2016-02-19; view: 305; Нарушение авторских прав