Сила Ампера. Взаимодействие проводников с током

Силой Ампера называется сила, действующая на проводник с током в магнитном поле.

Если проводник, по которому течет ток I, находится в поле, магнитная индукция которого равна , то на каждый из носителей тока в проводнике действует сила Лоренца. Сила Ампера является результирующей всех сил Лоренца.

Найдем величину силы Ампера , действующей на элемент тока малый настолько, что поле вблизи него можно считать однородным (рис. 29). Пусть в элементе тока содержится N носителей тока, на каждый из которых действует сила Лоренца (рис. 30). Величина силы Ампера равна сумме сил Лоренца, поэтому

. (2.12)

Число носителей тока выразим через их концентрацию n:

,

где dl – длина; S – площадь поперечного сечения элемента с током.

Формула для силы Лоренца имеет вид

.

Подстановка двух последних формул в (2.12) дает

.

Заметим, что 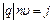– плотность тока, а – сила тока в проводнике. Тогда

.

Принимая во внимание, что – угол между и сила Ампера может быть записана в векторном виде следующим образом:

. (2.13)

Вычислим силу взаимодействия двух параллельных бесконечно длинных прямых проводников с током в вакууме (рис. 31).

На элемент тока , находящийся в магнитном поле тока , действует сила Ампера

. (2.14)

Ток в месте нахождения элемента (подразд. 1.3) создает магнитное поле, индукция которого

где b – расстояние между проводниками.

На элемент тока , находящийся в магнитном поле тока действует сила Ампера

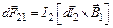. (2.16)

Формула для индукции магнитного поля тока в месте нахождения элемента тока (подразд. 1.3) имеет вид

(2.17)

Из (2.14), (2.15), а также (2.16), (2.17) следует:

;

.

Таким образом, сила взаимодействия на единицу длины проводника пропорциональна произведению сил токов и обратно пропорциональна расстоянию b между проводниками:

.

Полученные результаты находятся в полном согласии с экспериментальным законом Ампера (подразд. 1.1). На рис. 31 видно, что токи противоположного направления отталкиваются. В случае токов одного направления должно наблюдаться, как следует из формул (2.14) и (2.16), взаимное притяжение проводников.

Date: 2016-02-19; view: 537; Нарушение авторских прав