Неполные квадратные уравнения, их решение

Неполные квадратные уравнения бывают трёх видов.

Повторим теорию и рассмотрим примеры решения неполных квадратных уравнений каждого вида.

I. Неполные квадратные уравнения, к которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (илиax²-c=0).

Неполное квадратное уравнение такого вида либо имеет два корня, которые отличаются только знаками (являются противоположными числами), либо не имеет корней.

1. Если знаки a и c — разные, уравнение имеет два корня.

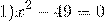
Раскладываем левую часть уравнения по формуле разности квадратов:

Это уравнение — типа «произведение равно нулю». приравниваем к нулю каждый множитель:

Ответ: 7; -7.

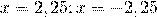
Ответ: 2,25; -2,25.

2. Если знаки a и c — одинаковые, уравнение не имеет корней.

Корней нет, так как сумма положительных чисел не может равняться нулю.

Ответ: нет корней.

Корней нет, так как сумма отрицательных чисел не может равняться нулю.

Ответ: нет корней.

В курсе алгебры 8 класса, после изучения квадратных корней, эти уравнения обычно решают приводя к виду x²=d:

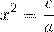
Примеры.

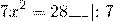
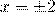
Ответ:±2.

Чтобы избавиться от иррациональности в знаменателе, умножаем и числитель, и знаменатель на √11:

Ответ:

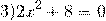
Корней нет, так как квадратный корень не может равняться отрицательному числу.

Ответ: нет корней.

Нет корней, так как квадратный корень не может быть равным отрицательному числу.

Ответ: нет корней.

II. Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.

Такие уравнения решаются разложением левой части уравнения на множители.

Общий множитель x выносим за скобки:

Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

Второе уравнение — линейное. Решаем его:

Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.

Примеры.

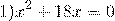
Общий множитель x выносим за скобки:

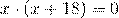
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

Ответ: 0; -18.

Общий множитель 5x выносим за скобки:

Приравниваем к нулю каждый множитель:

Ответ: 0; 3.

III. Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0.

Уравнение такого рода имеет единственный корень x=0

В некоторых учебниках считается, что уравнение имеет два одинаковых корня, каждый из которых равен нулю:

Примеры.

Ответ: 0.

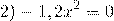
Ответ: 0.

Ответ: 0.

Date: 2016-02-19; view: 652; Нарушение авторских прав