Силы инерции при криволинейном движении точки

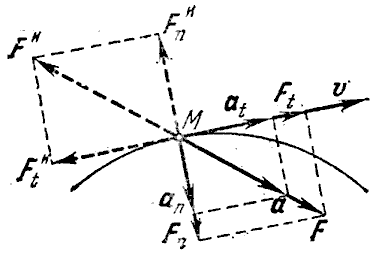
Рисунок 2 – Действия сил на точку при ее движении по криволинейной поверхности

В общем случае движения точки по криволинейной траектории ускорение точки “а”, как мы знаем, удобно разлагать на две составляющие: касательное ускорение а_t, направленное по касательной к траектории движения, и нормальное ускорение a_n, направленное по нормали к центру кривизны траектории. Положим, что к свободной материальной точке “М” массы “m”, движущейся со скоростью “V”, приложена сила “F”, направление которой образуете направлением скорости “V” некоторый угол (рис. 2). Точка в этом случае будет двигаться по криволинейному пути с ускорением а = F/m, направленным одинаково с силой F. Разложим его на составляющие ускорения: касательное, численно равное a_t=dV/dt — производной от модуля скорости точки по времени, и нормальное, равное по модулю а_n =V²/р, где р — радиус кривизны траектории в данном положении материальной точки.

Очевидно, что при криволинейном движении точки приоженную к ней силу “F” можно разложить на две составляющие: касательную силу F_t = mа_t, изменяющую модуль скорости точки, и нормальную силу F_n = mа_n, изменяющую направление скорости точки. При криволинейном движении точки ее силу инерции также можно разложить на две составляющие: касательную силу инерции F_t^и = - ma_t, направленную противоположно касательному ускорению точки, и нормальную силу инерции F_n^и = - mа_n, направленную противоположно нормальному ускорению точки.

17. Кинетоста́тика (от греч. kinetós — движущийся и Статика) — раздел механики, в котором рассматриваются способы решения динамических задач с помощью аналитических или графических методов статики. В основе кинетостатики лежит принцип Д’Аламбера, согласно которому уравнения движения тел можно составлять в форме уравнений статики, если к фактически действующим на тело силам и реакциям связей добавить силы инерции.

Методы кинетостатики находят применение при решении ряда динамических задач, особенно в динамике машин и механизмов. Так они используются при расчётах механизмов на прочность для нахождения сил реакций при известных заранее законах изменения положения частей механизма в пространстве

иференцируя по времени уравнение плоского движения тела 2 раза, можно получить ускарение полюса и угловое ускарение тела.

х=х_а(t) a_Ax=d²x_a/dt²

y=x_y(t) a_Ay=d²y_a/dt²

ϕ=ϕ(t) Ɛ=d² ϕ/dt²

Ɛ=d² ϕ/dt²

Чтобы получить ускарение любой другой точки тела представим плоское движение тела в виде комбинации поступ. движении вместе с полюсом (переносное движение) и вращение вокруг полюса (относительное движение).

18. Принцип возможных (виртуальных) перемещений – один из основных принципов механики, выражающий общее условие равновесия механической системы. Этот принцип широко используется при статистических исследованиях материальных систем, причем действие наложенных на систему связей учитывается введением соответствующих реакций связей.
Существуют две различные формулировки принципа возможных перемещений. В одной формулировке утверждается, что для равновесия материальной системы необходимо, чтобы равнялась нулю сумма элементарных работ всех внешних сил, приложенных к системе, на любом возможном перемещении. Так, например, в работе [12, с.319] принцип возможных перемещений формулируется следующим образом: “Необходимое и достаточное условие равновесия системы, подчиненной стационарным идеальным связям, заключается в равенстве нулю суммы элементарных работ задаваемых сил на любом возможном перемещении системы из рассматриваемого положения равновесия”.

19. ОБОБЩЁННЫЕ КООРДИНАТЫ

- независимые между собой параметры q_i (i = 1, 2,..., s)любойразмерности, число к-рых равно числу s степеней свободы механич. <системы и к-рые однозначно определяют положение системы. Закондвижениясистемы в О. к. даётся s ур-ниями вида q_i = q_i(t), где t - время.

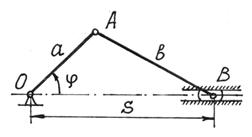
Степень свободы определяется числом независимых переменных (например, температура, концентрация сплава, давление), которые можно изменять в определенных пределах, не нарушая равновесия. Положение точек кривошипно-шатунного механизма (рис.70) можно определить заданием угла поворота 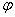кривошипа или расстоянием s, определяющим положение ползуна В (при ).

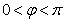Положение сферического маятника (рис.71) определяется заданием двух параметров, углов 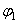и .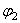

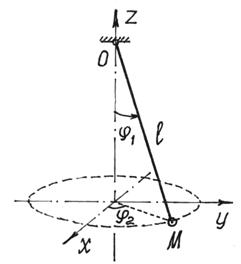
Минимальное количество независимых друг от друга обобщенных координат, которых достаточно, чтобы полностью и однозначно определить положение всех точек системы, называют числом степеней свободы этой системы.

Вообще для любой материальной системы можно назначить несколько обобщенных координат. Например, у кривошипно-шатунного механизма (рис.70) указаны две обобщенные координаты 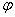и 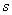. Но это не значит, что у механизма две степени свободы, так как одну координату можно определить через другую:

.

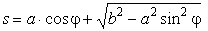21. Уравнениями Лагранжа второго рода называют дифференциальные уравнения движения механической системы, получаемые при применении лагранжева формализма. Если голономная механическая система описывается лагранжианом 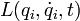( 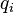— обобщённые координаты, t — время, точкой обозначенодифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид

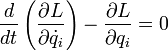
где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы.

Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид

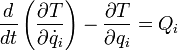
где 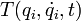— кинетическая энергия системы, 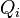— обобщённая сила.

Уравнения Лагранжа в механике получаются из законов динамики Эйлера (баланса количества движения и момента количества движения) при определенных ограничениях на систему (в ней должны присутствовать лишь идеальные голономные связи). Для других случаев получаются модификации уравнений Лагранжа. Отметим, что это частный (хотя и очень важный) случай механических систем.

Если для рассматриваемой системы применим принцип наименьшего действия, то вывод можно провести иначе. В лагранжевой механике вывод уравнений Лагранжа происходит на основе принципа наименьшего действия. Механическая система может быть описана некой функцией 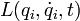, называемой лагранжианом. Лагранжиан - это разность кинетической и потенциальной энергий системы. Принцип наименьшего действия гласит, что функционал

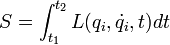
называемый действием принимает минимальное значение на траектории системы (здесь t₁ и t₂ — начальный и конечный моменты времени). Заметим, что необходимо доказать применимость принципа наименьшего действия к рассматриваемой системе: далеко не все физические системы ему подчиняются. Применяя к функционалу действию стандартную схему оптимизации, получаем для него уравнения Лагранжа — Эйлера, которые и называются уравнениями Лагранжа второго рода для механической системы.

Вывод уравнений для системы с одной обобщенной координатой и скоростью

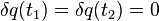
Изменение действия при переходе из состояния 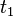в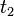

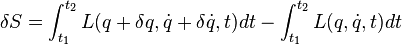
Разлагая эту разность по степеням

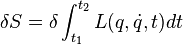
Варьируя это выражение, получаем:

Первое слагаемое заменяется по формуле Ньютона-Лейбница. Второе интегрируем по частям замечая что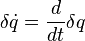

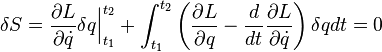
Первое слагаемое равно нулю исходя из самой первой формулы вывода. Второе слагаемое может быть равно нулю только если подынтегральное выражение равно нулю. Оно и является искомым уравнением Лагранжа:

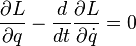
Date: 2016-02-19; view: 2655; Нарушение авторских прав