
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение числа групп
|
|
Число групп приближенно определяется по формуле Стэрджесса
n = 1 + 3,2 ž lg N,
где n – число групп, N – число единиц совокупности.
Здесь получаем: n = 1 + 3,2 ž log26 = 5,7
Ширина интервала составит: 6
,
где Xmax - максимальное значение группировочного признака в совокупности, Xmin - минимальное значение группировочного признака.
Здесь имеем: 

Определим границы группы.
| Номер группы | Нижняя граница | Верхняя граница |
| 365.8 | ||
| 365.8 | 418.6 | |
| 418.6 | 471.4 | |
| 471.4 | 524.2 | |
| 524.2 | ||
Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.
Для каждого значения ряда подсчитаем, какое количество, раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 313 - 365.8 | ||
| 313 - 365.8 | ||
| 313 - 365.8 | ||
| 313 - 365.8 | ||
| 313 - 365.8 | ||
| 365.8 – 418.6 | ||
| 365.8 – 418.6 | ||
| 365.8 – 418.6 | ||
| 418.6 – 471.4 | ||
| 418.6 – 471.4 | ||
| 418.6 – 471.4 | ||
| 471.4 – 524.2 | ||
| 471.4 – 524.2 | ||
| 524.2 - 577 | ||
| 577 - 630 |
Результаты группировки оформим в виде таблицы:
| Группы | № совокупности | Частота fi |
| 313 - 365.8 | 1,2,3,4,5 | |
| 365.8 – 418.6 | 6,7,8 | |
| 418.6 – 471.4 | 9,10,11 | |
| 471.4 – 524.2 | 12,13 | |
| 524.2 - 577 | ||
| 577 - 630 |
Построим гистограмму для полученного интервального ряда:

Таблица для расчета показателей.
| Группы | xi | Кол-во, fi | xi * fi | Накопленная частота, S | |x - хср|*f | (x - хср)2*f | Частота, fi/n |
| 313 - 365.8 | 339,4 | 0,83 | |||||
| 365.8 – 418.6 | 392,2 | 1176,6 | 99,6 | 3306,72 | 0,5 | ||
| 418.6 – 471.4 | 58,8 | 1152,48 | 0,5 | ||||
| 471.4 – 524.2 | 497.8 | 995.6 | 144,8 | 10483,52 | 0,33 | ||
| 524.2 - 577 | 550.6 | 550.6 | 125,2 | 15675,04 | 0,17 | ||
| 577 - 630 | 603.6 | 603.6 | 178,2 | 31755,24 | 0,17 | ||
| Итого: | 2828.6 | 6723.5 | 1036,6 | 2,5 |
Для оценки ряда распределения найдем следующие показатели:
Показатели центра распределения.
Средняя взвешенная
.
Здесь имеем: 

Модальная численность
Модальная численность - наиболее часто встречающееся значение признака у единиц данной совокупности.
,
где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.
Выбираем в качестве начала интервала 332, так как именно на этот интервал приходится наибольшее количество.

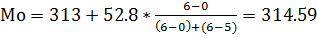
Наиболее часто встречающееся значение ряда – 314.59
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.
В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 313 – 365.8, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
.
Здесь имеем: 
ВЫВОД: Таким образом, 50% единиц совокупности будут меньше по величине 564.54
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 630 - 313 = 317
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
или 
ВЫВОД: Каждое значение ряда отличается от другого в среднем на 69.11.
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

Среднее квадратическое отклонение (средняя ошибка выборки).

Каждое значение ряда отличается от среднего значения 425.4 в среднем на 81.4
Относительные показатели вариации.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

ВЫВОД: Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.

ОТВЕТ:
Средняя численность занятых – 425 человек.
Модальная численность равна 314.59. Медиана равна 564.54.
Показатели вариации:
 размах вариации R = 317;
размах вариации R = 317;
 cреднее линейное отклонение d = 69.11;
cреднее линейное отклонение d = 69.11;
 дисперсия D = 6623.53;
дисперсия D = 6623.53;
 среднее квадратическое отклонение s = 81.4;
среднее квадратическое отклонение s = 81.4;
 коэффициент вариации v = 19.13 %;
коэффициент вариации v = 19.13 %;
 линейный коэффициент вариации Kd = 16.25 %.
линейный коэффициент вариации Kd = 16.25 %.
Задание 2
Имеются данные о производстве промышленной продукции на предприятии за 1995-2000 г.г. млн. руб.
| 503+ N | 369 + N | 321 + N | 120 + N | 165 + N | 129 + N |
Рассчитайте и проанализируйте следующие показатели ряда динамики:
— средний уровень ряда;
— цепные и базисные абсолютный прирост, коэффициент роста и темпы прироста.
По итогам расчетов сделать выводы.
РЕШЕНИЕ: Подставим в таблицу N = 26 и получим следующие данные:
Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными.
Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким способом показатели динамики называются цепными.
Важнейшим статистическим показателем динамики является абсолютный прирост, который определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации.
Абсолютный прирост
цепной прирост: ∆yц = yi - yi-1
базисный прирост: ∆yб = yi - y1
Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Темп прироста
цепной темп прироста: Tпрцi = ∆yi / yi-1
базисный темп прироста: Tпpб = ∆yбi / y1
Темп роста характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах.
Темп роста
цепной темп роста: Tpцi = yi / yi-1;
базисный темп роста: Tpб = yбi / y1
Абсолютное значение 1% прироста
цепной: 1%цi = yi-1 / 100%;
базисный: 1%б = yб / 100%
Темп наращения
Важным статистическим показателем динамики социально-экономических процессов является темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала
Tн = ∆yцi / y1
Цепные показатели ряда динамики.
Таблица 1.
| Период | Производство промышленной продукции на предприятии | Абсолютный прирост | Темп прироста, % | Темпы роста, % | Абсолютное содержание 1% прироста | Темп наращения, % |
| - | - | 5.29 | ||||
| -134 | -25.33 | 74.67 | 5.29 | -25.33 | ||
| -48 | -46.08 | 87.85 | 3.95 | -34.41 | ||
| -201 | -57.93 | 42.08 | 3.47 | -38 | ||
| 30.82 | 130.82 | 1.46 | 8.51 | |||
| -36 | -18.85 | 81.15 | 1.91 | -6.81 |
ВЫВОД: Таким образом, в 2000 г. по сравнению с 1999 г. производство промышленной продукции на предприятии уменьшилось на 36 млн. руб. или на 17.14%
Максимальный прирост наблюдается в 1999 (45 млн. руб.)
Минимальный прирост зафиксирован в 1998 (-201 млн. руб.)
Темп наращения показывает, что тенденция ряда убывающая, что свидетельствует о замедлении производства промышленной продукции на предприятии.
Базисные показатели ряда динамики. Таблица 2.
| Период | Производство промышленной продукции на предприятии | Абсолютный прирост | Темп прироста, % | Темпы роста, % |
| - | - | |||
| -134 | -25.33 | 74.67 | ||
| -182 | -34.41 | 65.60 | ||
| -383 | -72.40 | 27.60 | ||
| -338 | -63.89 | 36.11 | ||
| -374 | -70.70 | 29.30 |
ВЫВОД: В 2000 по сравнению с 1995 производство промышленной продукции на предприятии уменьшилось на 374 млн. руб. или на 70.70%
Расчет средних характеристик рядов.
Для нахождения среднего уровня моментного ряда используют среднюю хронологическую:

ВЫВОД: Среднее значение производства промышленной продукции на предприятии за анализируемый период составило 284.2 млн. руб.
Средний темп роста вычисляется по формуле
.
Здесь имеем: 
ВЫВОД: В среднем за весь период рост анализируемого показателя составил 0.78
Средний темп прироста вычисляется по формуле
.
Здесь имеем: 

ВЫВОД: В среднем с каждым периодом производство промышленной продукции на предприятии сокращалось на 22%.
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики.
Средний абсолютный прирост вычисляется по формуле
.
Здесь имеем: 
ВЫВОД: С каждым периодом производство промышленной продукции на предприятии в среднем уменьшалось на 74.8 млн. руб.
Задание 3
Имеются следующие данные о продаже овощей и ценах на них.
| Овощи | Периоды | |||
| Базисный | Отчетный | |||
| количество, т | цена 1кг, руб. | количество, т | цена 1кг, руб. | |
| свекла | 64.3 + N | 22 + N | 52.7 + N | 24 + N |
| капуста | 41.0 + N | 18 + N | 38.8 + N | 21 + N |
| морковь | 89.2 + N | 13 + N | 91.0 + N | 7 + N |
Рассчитайте и проанализируйте:
1) индивидуальные индексы цен и количеств (физического объема), товарооборота;
2) общий агрегатный индекс цен;
3) общий агрегатный индекс количеств (физического объема);
4) общий агрегатный индекс стоимости (товарооборота).
По итогам расчетов сделать выводы.
РЕШЕНИЕ: Подставим в таблицу N = 26 и получим следующие данные:
| Овощи | Периоды | |||
| Базисный | Отчетный | |||
| количество, т | цена 1кг, руб. | количество, т | цена 1кг, руб. | |
| свекла | 90.3 | 48.0 | 78.7 | 50.0 |
| капуста | 67.0 | 44.0 | 64.8 | 47.0 |
| морковь | 115.2 | 39.0 | 117.0 | 33.0 |
1) Сравнение цен одного товара осуществляется с помощью индивидуального индекса цен.

где Pi0– цена i-гo товара в базисном периоде, Рi1 – цена i-гo товара в отчетном периоде.
Найдем индивидуальные индексы цен овощей:
— для свеклы: 
или 104%, т.е. цена проданной свеклы в отчетном году увеличилась по сравнению с базисным на 4%.
— для капусты: 
или 106%, т.е. цена проданной капусты в отчетном году увеличилась по сравнению с базисным годом на 6 %.
— для моркови: 
или 85%, т.е. цена проданной моркови в отчетном году уменьшилась по сравнению с базисныи годом на 15%.
Найдем индивидуальный индекс физического объема реализации с помощью формулы:

где qi0– количество i-гo товара в базисном периоде, qi1 – количество i-гo товара в отчетном периоде.
Найдем индивидуальные индексы количеств:
— для свеклы: 
или 87%, т.е. количество тонн проданной свеклы в отчетном году уменьшилось по сравнению с базисным на 13%;
— для капусты: 
или 97%, т.е. количество тонн проданной капусты в отчетном году уменьшилось по сравнению с базисным на 3%;
— для моркови: 
или 102 %, т.е. количество тонн проданной моркови в отчетном году увеличилось по сравнению с базисным на 2%;
Аналогично, найдем индивидуальные индексы товарооборота:
— для свеклы: 
— для капусты: 
— для моркови:  .
.
Вывод: товарооборот в отчетном году по сравнению с базисным годом: для свеклы – уменьшился на 9%; для капусты – увеличился на 3 %; для моркови – уменьшился на 9%.
Индивидуальные индексы объемных и качественных показателей, взаимосвязаны между собой так же индексы: произведение индекса физического объема товарооборота на индекс цен, дает индекс товарооборота:

Проверка: для свеклы – 1,04 * 0,87 = 0,91;
для капусты – 1,06 * 0,97 = 1,03;
для моркови – 0,85 *1,02 = 0,87.
2) Найдем общий агрегатный индекс цен (метод Пааше)
.


∆Zp = ∑q1 • p1 - ∑q1 • p0
∆Zp = 10841.6 – 11191.8 = -350.2
Вывод: За счет изменения цен сводный товарооборот снизился на 3.13% или на 350.2 руб.
3) Найдем общий агрегатный индекс количеств (физического объема) для овощей. Общий агрегатный индекс физического объема продукции (индекс Ласпейреса)

∆Zq = ∑q1 • p0 - ∑q0 • p0
∆Zq = 533871 – 517570,56 = 16300,44
Вывод: За счет изменения объема проданной продукции, товарооборот увеличился на 3,15% или на 16 300,44 руб.
4) Найдем общий агрегатный индекс товарооборота:

∆Z = ∑q1 • p1 - ∑q0 • p0
∆Z = 451737 – 517570.56 = -65833.56
Вывод: За счет всех факторов общий товарооборот снизился на 12.71% или на 65 833.56 руб.
Покажем взаимосвязь индексов Ipq = Iq • Ip = 1.03 • 0.97  1.
1.
ОТВЕТ:
Индивидуальные индексы цен: для свеклы: 1.04; для капусты: 1.06; для моркови: 0.85. Индивидуальные индексы количеств: для свеклы: 0.87; для капусты: 0.97; для моркови: 1.02. Индивидуальные индексы товарооборота: для свеклы: 0.91; для капусты: 1.03; для моркови: 0.87.
За счет изменения цен сводный товарооборот снизился на 3.13% или на 350.2 руб. За счет изменения объема проданной продукции, товарооборот увеличился на 3,15% или на 16 300,44 руб. За счет всех факторов общий товарооборот снизился на 12.71% или на 65 833.56 руб.
Задание 4
Численность работников предприятия, начавшего свою деятельность с 10 мая по списку составляла: 10-21 мая — 220 человек; 22-25 мая — 210 человек; 26-31 мая — 205 человек. Среднесписочная численность работников составляла, чел.:
июнь — 210;
3 квартал — 225;
октябрь — 245;
ноябрь — 240;
декабрь — 242.
Определите среднюю численность работников предприятия за: май; 2 квартал; I полугодие; 4 квартал; II полугодие; год.
РЕШЕНИЕ: Занесем данные из условия в следующую таблицу:
| Численность работников предприятия | |||||||
| май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь |
| 10 - 21 | III квартал | ||||||
| 22 - 25 | |||||||
| 26 - 31 | |||||||
| Средне-списочная численность |
Определим среднюю численность работников за май:
 человек.
человек.
Определим среднюю численность работников за 2 квартал (май и июнь, т.к. в апреле предприятие еще не действовало):
 человек.
человек.
Определим среднюю численность работников за I полугодие (май и июнь, т.к. в январе-апреле предприятие еще не действовало):
 человек.
человек.
Определим среднюю численность работников за IV квартал (октябрь, ноябрь, декабрь):
 человек.
человек.
Определим среднюю численность работников за II полугодие (июль-декабрь):
 человека.
человека.
Определим среднюю численность работников за год (май - декабрь):
 человек.
человек.
ОТВЕТ: средняя численность работников предприятия: за май – 212 человек; за 2 квартал – 219 человек; за I полугодие – 219 человек; за 4 квартал – 242 человек; за II полугодие – 234 человек; за год – 226 человек.
Задание 5.
Имеются следующие данные по основным фондам предприятия за 2010 год, тыс. руб.:
| Основные фонды по полной балансовой стоимости на начало года | 1120 + N |
| Коэффициент износа на начало года, % | 53 + N |
| В течение года введено новых основных фондов | 40 + N |
| Выбыло основных фондов (полная балансовая стоимость) | 70 + N |
| Остаточная стоимость выбывших основных фондов | 15 + N |
| Сумма начисленного износа основных фондов за год | 104 + N |
| Среднегодовая стоимость основных производственных фондов | 1076 + N |
| Объем произведенной продукции | 1036 + N |
Постройте баланс основных фондов и определите:
1) наличие основных фондов на конец года по полной и остаточной стоимости;
2) коэффициенты обновления и выбытия основных фондов;
3) коэффициенты износа и годности основных фондов на начало и конец года;
4) показатели, характеризующие использование основных фондов.
РЕШЕНИЕ:
Подставим N = 26 и получим:
| Основные фонды по полной балансовой стоимости на начало года | 1146 тыс. руб. |
| Коэффициент износа на начало года, % | 79 % |
| В течение года введено новых основных фондов | 66 тыс. руб. |
| Выбыло основных фондов (полная балансовая стоимость) | 96 тыс. руб. |
| Остаточная стоимость выбывших основных фондов | 41 тыс. руб. |
| Сумма начисленного износа основных фондов за год | 130 тыс. руб. |
| Среднегодовая стоимость основных производственных фондов | 1102 тыс. руб. |
| Объем произведенной продукции | 1062 тыс. руб. |
1) Считаем полную стоимость на конец года
§ 1. Наличие на начало года по полной стоимости 1146
§ 2. Поступило в отчетном году 66
§ 3. Выбыло в отчетном году по полной стоимости 96
Наличие на конец года по полной стоимости: 1146 + 66 – 96 = 1116 тыс. руб.
Считаем остаточную стоимость на конец года
§ 1. Остаточная стоимость фондов на начало года 1146
§ 2. Поступление основных фондов 66
§ 3. Выбытие по остаточной стоимости 41
§ 4. Амортизация 130
Наличие на конец года по остаточной стоимости: 1146 + 66 – 96 –130 = 986 тыс. руб.
2) Коэффициент обновления, выбытия:
§ К поступления (обновления) = ОФ введенные / ОФ на конец года = 66 / 1116 = 0.059.
§ К выбытия = ОФ выбывшие / ОФ на начало год = 96 / 1146 = 0.08.
3) Коэффициенты годности и износа
§ К годности н.г. = стоимость ОФ за вычетом износа / полная стоимость ОФ = (1146 - 1146*79%) / 1146 = 240.66/1146 = 0,21 или 21%.
§ К годности к.г. = (135.66 / 1116 = – 0,12 или 12%.
§ К износа н.г. = сумма износа / полная стоимость основных фондов = (1165-240.66) / 1165 = 0,98 или 98 %.
§ К износа к.г. = (1135-(-100,7)) / 1135 = 1,089 или 108,9 %.
4) Показатели, характеризующие использование основных фондов.
§ фондоотдача = выпуск продукции / ср.год. полн. стоимость ОФ = 1081/1121 = 0,96 выпуск продукции на 1 тыс. руб.
§ фондоемкость = ср.год. полн. стоимость ОФ / выпуск продукции = 1021/1081 = 1,03 доля стоимости основных фондов, приходящихся на каждую тыс. рублей выпускаемой продукции.
Баланс основных фондов
| Виды ОФ в группир. по различным признакам | Наличие на начало года | В течение года | Наличие на конец года | |||
| ввод в действие ОФ | прочие поступления | выбытие по ветхости и износу | прочие выбытия | |||
| 6 = 1+2+3-4-5 | ||||||
| ОФ | – |
Баланс по первоначальной стоимости за вычетом износа
| Виды ОФ в группир. по различным признакам | Наличие на начало года | В течение года | Наличие на конец года | |||
| ввод в действие ОФ | прочие поступления | выбытие по ветхости и износу | прочие выбытия | |||
| 6 = 1+2+3-4-5 | ||||||
| ОФ | 23,30 | – | -100,7 |
Задание 6
Имеются следующие данные о цене продаж товаров (руб.) по месяцам года. С целью выявления тренда, проведите аналитическое выравнивание указанного параметра рынка по прямой, представив уравнение трендовой модели.
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | Июль | Август | Сентябрь | Октябрь | Ноябрь | Декабрь |
| Цена |
РЕШЕНИЕ:
Линейное уравнение тренда имеет вид y = bt + a
Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y•t
| t | y | t2 | y2 | t y |
Для наших данных система уравнений имеет вид:
 12a0 + 78a1 = 573
12a0 + 78a1 = 573
78a0 + 650a1 = 3867
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = 0.997, a1 = 41.273
Уравнение тренда:
y = 0.997 t + 41.273
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = 0.997 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 месяц, y изменится в среднем на 0.997.

Анализ точности определения оценок параметров уравнения тренда.
где m = 1 - количество влияющих факторов в модели тренда.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (10;0.025) = 2.228
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 7
(41.27 + 1*7 - 2.228*61.64; 41.27 + 1*7 - 2.228*61.64)
(-13.39;109.89)
Проверка гипотез относительно коэффициентов линейного уравнения тренда.
t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента b не подтверждается
Статистическая значимость коэффициента a подтверждается
Доверительный интервал для коэффициентов уравнения тренда.
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими:
(b - tнабл Sb; b + tнабл Sb)
(0.997 - 2.228•2.22; 0.997 + 2.228•2.22)
(-3.95;5.94)
Так как точка 0 (ноль) лежит внутри доверительного интервала, то интервальная оценка коэффициента b статистически незначима.
(a - tнабл Sa; a + tнабл Sa)
(41.273 - 2.228•16.35; 41.273 + 2.228•16.35)
(4.85;77.69)
ОТВЕТ:
Уравнение тренда имеет вид: y = 0.997 t + 41.273.
Задание 7
При проверке импортируемого товара на таможне методом случайной повторной выборки было отобрано 500 изделий. В результате был установлен средний вес изделия 70 + N г при среднеквадратическом отклонении 11 г. С вероятностью 0,997 определите пределы, в которых находится средний вес в генеральной совокупности.
РЕШЕНИЕ:
При N = 26 имеем средний вес изделия:  = 70+26=96 г; s = 11; n =500.
= 70+26=96 г; s = 11; n =500.
Доверительный интервал для генерального среднего.
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) = γ
Ф(tkp) = γ/2 = 0.997/2 = 0.4985
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.4985
tkp(γ) = (0.4985) = 2.96
(96 - 32.56; 96 + 32.56) = (63.44; 128.56)
С вероятностью 0.997 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
ОТВЕТ:
Средний вес в генеральной совокупности находится в пределах (63.44; 128.56) с вероятностью 0,997.
Задание 8
Имеются следующие данные о квалификации и заработной плате рабочих.
| Табельный номер | ||||||||||
| Разряд | ||||||||||
| Заработная плата, тыс. руб. | 58+N | 64+N | 89+N | 98+N | 72+N | 49+N | 71+N | 59+N | 68+N | 52+N |
Для характеристики связи между рассматриваемыми признаками исчислить:
1) линейное корреляционное уравнение;
2) линейный коэффициент корреляции;
3) индекс корреляции.
РЕШЕНИЕ: Подставим в таблицу N = 26 и получим следующие данные:
| Табельный номер | ||||||||||
| Разряд | ||||||||||
| Заработная плата, тыс. руб. |
1) Используем графический метод для наглядного изображения формы связи между изучаемыми показателями. Для этого в прямоугольной системе координат строим график, по оси ординат откладывают индивидуальные значения результативного признака Y (заработная плата), а по оси абсцисс - индивидуальные значения факторного признака X (разряд). Совокупность точек результативного и факторного признаков называется полем корреляции.


На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер. Линейное уравнение регрессии имеет вид
y = bx + a + ε
Для оценки параметров - используем МНК (метод наименьших квадратов).
Формально критерий МНК можно записать так:
S = ∑(yi - y*i)2 → min
Система нормальных уравнений.
 a•n + b∑x = ∑y
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
 10a + 35b = 1130
10a + 35b = 1130
35a + 141b = 4120
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 8.9189, a = 81.7838
Таким образом, уравнение регрессии (эмпирическое уравнение регрессии):
y = 8.9189 x + 81.7838
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | y | x2 | y2 | x • y |
Параметры уравнения регрессии.
Выборочные средние.
;  ;
; 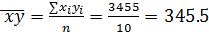 ;
;
Выборочные дисперсии:
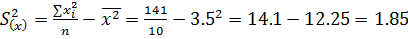 ;
;

Среднеквадратическое отклонение
;
2) Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
вариация динамика коэффициент индекс

Вывод: В нашем примере связь между признаком Y фактором X высокая и прямая.
Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 8.92 x + 81.78
Коэффициентам уравнения линейной регрессии можно придать экономический смысл.
Коэффициент регрессии b = 8.92 показывает среднее изменение заработной платы (в тыс. руб.) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением квалификации на 1 разряд y повышается в среднем на 8.92 тыс. руб.
Коэффициент a = 81.78 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная).
Вывод: в нашем примере связь прямая.
3) Индекс корреляции.
Для линейной регрессии индекс корреляции равен коэффициенту корреляции
rxy = 0.82.
Вывод: полученная величина свидетельствует о том, что фактор x существенно влияет на y
ОТВЕТ:
Линейное уравнение регрессии имеет вид y = 8.92 x + 81.78
Линейный коэффициент корреляции принимает значение rxy = 0.82.
Индекс корреляции равен коэффициенту корреляции, т.е. 0.82.
Размещено на Allbest.ru
| <== предыдущая | | | следующая ==> |
| | | Кто такая стерва? Эволюция вида |
Date: 2016-02-19; view: 2842; Нарушение авторских прав