
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Контрольных заданий
|
|
Задача 1.
Данная задача решается с помощью метода группировок. Группировка – это разбиение совокупности на группы, однородные по какому – либо признаку. Этапы построения группировки:
1. Определение группировочного признака;
2. Определение числа групп;
3. Определение интервала группировки (если длина интервала не задана, то определяем его по формуле для равных интервалов:  , где i – длина интервала,
, где i – длина интервала, 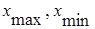 - это максимальное, минимальное значение признака у данной единицы совокупности; n – число групп);
- это максимальное, минимальное значение признака у данной единицы совокупности; n – число групп);
4. Разбиение совокупности на группы;
5. Оформление результатов в групповой таблице.
Задача 2.
Данная задача направлена на расчет средних величин. Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.
Виды средних величин:
1. Средняя арифметическая простая используется, когда известны варианты (x), имеющие равновеликие частоты (n) – 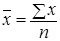 .
.
2. Средняя арифметическая взвешенная применяется, когда известны варианты, имеющие неравновеликие частоты (f) - 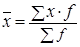 .
.
3. Средняя гармоническая простая применяется, когда вес каждого варианта равен единице -  .
.
4. Средняя гармоническая взвешенная применяется, когда неизвестны веса, а имеется произведение варианты на частоту -  .
.
Задача 3.
Задание решается с помощью выборочного метода. Выборочное наблюдение – это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю совокупность.
Для нахождения предельных ошибок выборки используются следующие формулы:
1. При повторном способе отбора:
- для средней количественного признака:
 , где
, где  - выборочная дисперсия (дисперсия признака в выборочной совокупности); n - объём выборки (число обследованных единиц);
- выборочная дисперсия (дисперсия признака в выборочной совокупности); n - объём выборки (число обследованных единиц);
t - где нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки;  - средняя ошибка выборки.
- средняя ошибка выборки.
- для доли (альтернативного признака):
 , где w - выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);
, где w - выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности);
2. При бесповторном способе отбора
- для средней количественного признака
 , где N - объем генеральной совокупности (число входящих в неё единиц);
, где N - объем генеральной совокупности (число входящих в неё единиц);
- для доли (альтернативного признака)
 .
. 
Необходимый объём выборки определяется по формулам.
При бесповторном способе отбора:
- для средней количественного признака  ;
;
- для доли (альтернативного признака) 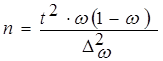 .
.
При повторном способе отбора:
- для средней количественного признака  ;
;
- для доли 
Задача 4.
Данная задача решается с помощь анализа рядов динамики. Формулы для расчета изменений от года к году следующие:
| Наименование показателя | Методы расчета | |
| С переменной базой (цепные) | С постоянной базой (базисные) | |
| 1. Абсолютный прирост (Dцеп; Dбаз.)* | Dцеп = y i – yi-1 | Dбаз = yi – y0 |
| 2. Коэффициент роста (Кр) | 
| 
|
| 3. Темп роста (Тр), % | Трц = Kрц * 100 | Трб = Крб * 100 |
| 4. Коэффициент прироста (Кпр) | Кпрц = Kрц – 1 | Кпрб = Крб – 1 |
| 5. Темп прироста (Тпр),% | Тпрц = Кпрц * 100 | Тпрб = Кпрб * 100 |
| 6. Абсолютное значение одного процента прироста (А%) | 
| 
|
Средние показатели за весь период определяются по формулам:
| Наименование показателя | Метод расчета |
1) Средний уровень ряда ( ):
а) для интервального ряда с:
- равными интервалами
- неравными интервалами ):
а) для интервального ряда с:
- равными интервалами
- неравными интервалами
|


|
| б) для моментного ряда с: - равными интервалами - неравными интервалами |
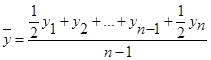

|
2) Средний абсолютный прирост (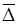 ) )
|  или или 
|
3) Средний коэффициент роста ( ) )
|  или или 
|
4) Средний темп роста (снижения) ( ), % ), %
| 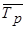 = = 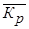 *100 *100
|
5) Средний темп прироста ( ), % ), %
|  = = 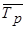 - 100 или - 100 или
 = ( = (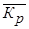 - 1)*100 - 1)*100
|
6)Среднее величина абсолютного значения 1% прироста ( ) )
| 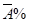 = = 
|
Задание 5.
Данная задача решается с помощью индексного метода.
Формулы для расчета:
 - общий индекс товарооборота,
- общий индекс товарооборота,
где p1 и p0 – цены единицы продукции в отчетном и базисном периодах соответственно;
q1 и q0 – количество продукции в отчетном и базисном периодах соответственно;
 - агрегатная форма общего индекса физического объёма;
- агрегатная форма общего индекса физического объёма;
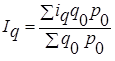 - среднеарифметическая форма общего индекса физического объёма, где
- среднеарифметическая форма общего индекса физического объёма, где 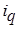 - индивидуальный индекс физического объёма;
- индивидуальный индекс физического объёма;
 - среднегармоническая форма общего индекса физического объёма;
- среднегармоническая форма общего индекса физического объёма;
 - агрегатная форма общего индекса цен;
- агрегатная форма общего индекса цен;
 - среднеарифметическая форма общего индекса цен, где
- среднеарифметическая форма общего индекса цен, где  - индивидуальный индекс цен;
- индивидуальный индекс цен;
 - среднегармоническая форма общего индекса цен;
- среднегармоническая форма общего индекса цен;
 - агрегатная форма общего индекса себестоимости продукции;
- агрегатная форма общего индекса себестоимости продукции;
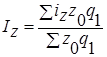 - среднеарифметическая форма общего индекса себестоимости продукции, где
- среднеарифметическая форма общего индекса себестоимости продукции, где 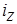 - индивидуальный индекс себестоимости продукции;
- индивидуальный индекс себестоимости продукции;
 - среднегармоническая форма общего индекса себестоимости продукции.
- среднегармоническая форма общего индекса себестоимости продукции.
СПИСОК ЛИТЕРАТУРЫ
1. Гусаров В. М. Статистика: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2008. – 463 с. Допущено МО РФ.
2. Ефимова М. Р., Петрова Е. В., Ганченко О. И. Практикум по общей теории статистики: Учеб. пособие. – М.: Юрайт, 2012.- 368 с.
3. Ефимова М.Р. и др. Общая теория статистики: Учеб. для студентов вузов/Ефимова М.Р., Петрова Е.В., Румянцев В.Н.- 2-е изд., испр. и доп.-М.:ИНФРА-М, 2011.- 416 с.
4. Курс социально-экономической статистики/ Учебно-практическое пособие/ Под. Ред. Назарова М.Г. - М: Омега-Л, 2010 г.- 1013 с. Рекомендовано МО РФ.
5. Рудакова, Р.П. Статистика: учеб. пособие для студентов вузов / Р. П. Рудакова, Л. Л. Букин, В. И. Гаврилов; под ред. И.И. Елисеевой. - 2-е изд. - СПб.: Питер, 2007. - 287 с.: табл. Допущено МО РФ.
6. Салин В. Н., Шпаковская Е. П. Социально-экономическая статистика: Учебник.- М.: КноРус, 2007. - 304 с. Допущено МО РФ.
7. Практикум по теории статистики: Учеб. пособие/ под ред. Р.А. Шмойловой. – 3-е изд., перераб. И доп. – М.: Финансы и статистика, 2008. – 416 с.
8. Статистика: учеб. для студентов вузов / И. И. Елисеева [и др.]; под ред. И.И.Елисеевой. - М.: Юрайт, 2011. – 496 с. Допущено МО РФ.
9. Теория статистики: учеб. для студентов экон. специальностей вузов / Р. А. Шмойлова [и др.]; Моск. гос. ун-т экономики, статистики и информатики (МЭСИ); под ред. Р.А.Шмойловой. - 5-е изд., доп. и перераб. - М.: Финансы и статистика, 2009. - 655, [1] с. - Рекомендовано МО РФ.
10. Харченко Н.М. Статистика: учебник для студентов вузов. - 2-е изд., перераб. и доп. - М.: Дашков и Ко, 2011. - 468с. Допущено МО РФ.
Date: 2016-02-19; view: 991; Нарушение авторских прав