
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Средняя длина свободного пробега молекул. Понятие о физическом вакууме
|
|

Рис. 19.1
Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Между двумя последовательными соударениями молекулы, двигаясь равномерно и прямолинейно, проходят некоторые расстояния, называемые длинами свободных пробегов l (рис. 19.1.а). Эти расстояния могут быть самыми разными, то есть l - случайная величина. Поэтому вводят понятие средней длины свободного пробега < l >, под которой понимают среднее расстояние, проходимое молекулой между двумя последовательными столкновениями со средней арифметической скоростью <V>.
Будем считать, что молекулы газа представляют собой шарики диаметром d. Минимальное расстояние (рис.19.1.б), на которое могут сблизиться при столкновении центры двух молекул, также равно d. Это расстояние называется эффективным диаметром молекулы. Круг радиусом d с центром в центре рассматриваемой молекулы площадью pd2 называется эффективным сечением молекулы.
Если молекула за некоторый промежуток времени Dt претерпевает в среднем < V > столкновений, то средняя длина ее свободного пробега равна
 . (19.1)
. (19.1)
Предположим для простоты, что движется только одна рассматриваемая молекула, а остальные неподвижны. Кроме того, ломаную траекторию молекулы мысленно спрямим и будем считать движение молекул условно прямолинейным (рис.19.1. в). Тогда за время Dt эта молекула претерпит < n > столкновений, равное числу молекул, центры которых лежат в прямом цилиндре с основанием, равным эффективному сечению молекулы, и высотой, равной пути, проходимому молекулой за это время, то есть <V> Dt:
 ,
,
где n - концентрация молекул, V - объем цилиндра.
Учитывая, что  , получим
, получим
 .
.
На самом же деле движутся все молекулы, и число столкновений определяется не средней арифметической скоростью молекул (то есть средней скоростью по отношению к стенкам сосуда), а средней скоростью их движения по отношению друг к другу <V отн. >, которая, как можно показать, больше средней арифметической скорости 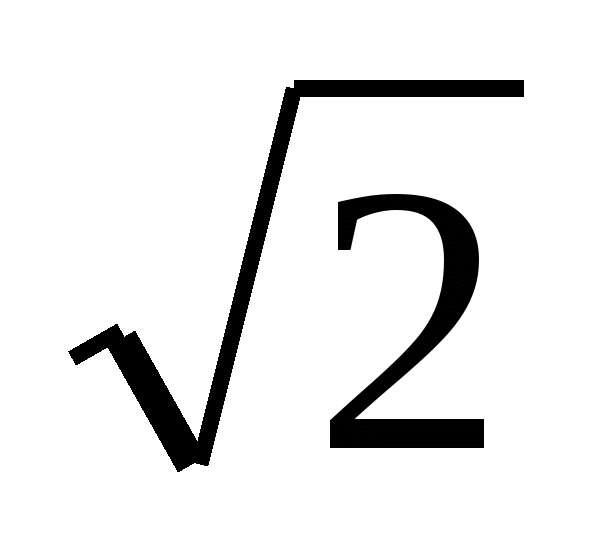 раз, то есть
раз, то есть
 .
.
Поэтому при учете движения всех молекул среднее число столкновений, испытываемых одной молекулой за некоторый промежуток времени Dt, равно
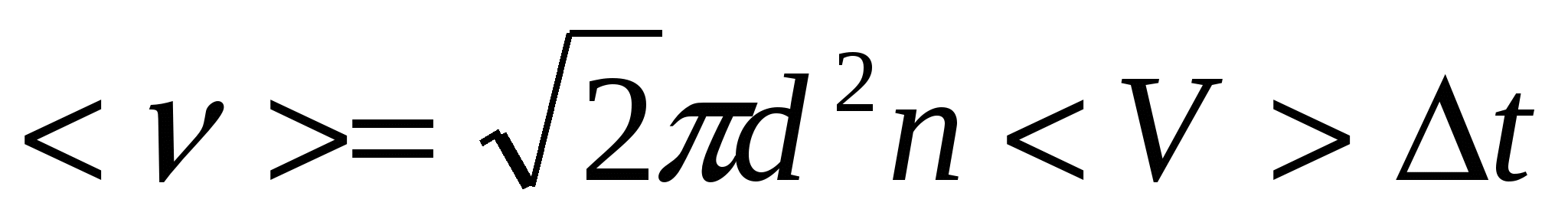 , (19.2)
, (19.2)
а в единицу времени
 . (19.3)
. (19.3)
Подставляя выражение(19.2) в (19.1), получим выражение для средней длины свободного пробега молекулы:
 (19.4)
(19.4)
Используется и иная форма записи выражения для < l >, для получения которой нужно в выражение (19.4) подставить n из уравнения (15.26), тогда
 (19.5)
(19.5)
Из выражения (19.5) следует, что с ростом давления газа p средняя длина свободного пробега уменьшается. Для примера укажем, что при нормальных условиях (p»105Па, Т=273К) молекулы кислорода движутся со средней скоростью порядка 500 м/с, имеют среднюю длину свободного пробега около 2*10-7м и совершают приблизительно 2,5.109столкновений в секунду каждая. В табл.19.1 приведены значения< l >для молекул кислорода при Т =293 К и различных давлениях.
Таблица 19.1
| < l > | P | |
| м | Па | мм.рт.ст. |
| 6,21*10-8 | 1,012*105 | |
| 4,72*10-5 | 1,333*102 | |
| 4,72*10-3 | 1,333 | 10-2 |
| 4,72*10-1 | 1,333*10-2 | 10-4 |
| 4,72*102 | 1,333*10-5 | 10-7 |
Как следует из таблицы, при малых давлениях значение < l >может быть больше размеров области (сосуда), в которой находится газ; в этом случае молекулы движутся от одной стенки сосуда до другой практически без столкновений друг с другом.
Date: 2016-02-19; view: 1281; Нарушение авторских прав