Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Кривые на плоскости
|
|
Алгебраическая кривая второго порядка: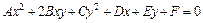 
, где числа 
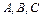- не равны нулю одновременно.
Классификация кривых второго порядка:
1) если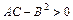 
, то общее уравнение определяет кривую эллиптического типа (окружность (при 
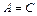), эллипс (при 
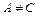), пустое множество, точку);
2) если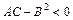 
, то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых);
3) если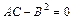 
, то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых).
Окружность, эллипс, гипербола и парабола являются невырожденными кривыми второго порядка.
Окружность. Каноническое уравнение окружности: 
, где 
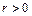радиус окружности, точка 
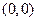- центр окружности.
Нормальное уравнение окружности: 
. Оно определяет окружность с центром в точке 
и радиусом 
.
Эллипс. Каноническое уравнение эллипса: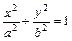 
, 
.
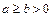Числа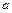 
и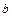 
- большая и малая полуоси эллипса; точки 
, 
, 
, 
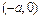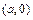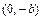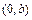- вершины; оси 
и 
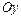- главные оси симметрии; точка 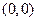- центр симметрии ( или просто центр) эллипса; прямоугольник со сторонами 
, 
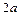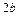параллельными главным осям симметрии и центром в точке 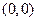- основной прямоугольник эллипса; точки 
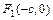и 
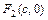, где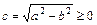 
- фокусы эллипса; векторы 
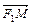и 
- фокальные радиус-векторы; числа 
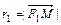и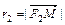 
- фокальные радиусы точки 
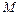, принадлежащей эллипсу; число 
(
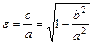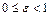) - эксцентриситет эллипса (при 
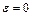эллипс является окружностью); прямые 
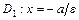и 
- директрисы эллипса.
Гипербола. Каноническое уравнение гиперболы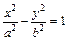 
, 
.
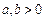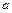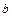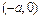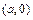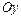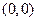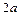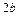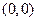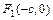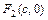Числа и - действительная и мнимая полуоси гиперболы; точки , - вершинами; оси и - главные оси симметрии; точка - центр симметрии ( или просто центр) гиперболы; прямоугольник со сторонами , параллельными главным осям симметрии и центром в точке - основной прямоугольник гиперболы; точки и , где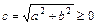 
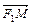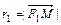- фокусы гиперболы; векторы и - фокальные радиус-векторы; числа и 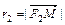- фокальные радиусы точки 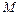, принадлежащей гиперболе; число 
(
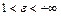) - эксцентриситет гиперболы; прямые 
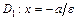и - директрисы гиперболы; прямые 
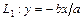и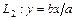 
называются асимптотами гиперболы (они проходят через противоположные вершины основного прямоугольника гиперболы).
Парабола. Каноническое уравнение параболы: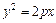 
, 
.
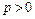Число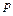 
- параметр параболы; ось - ось симметрии; точка – вершина параболы; точка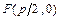 
- фокус параболы; вектор 
- фокальный радиус-вектор; число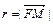 
- фокальный радиус точки 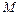, принадлежащей параболе; прямая 
- директриса параболы.
Плоскость.
1) 
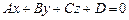- общее уравнение плоскости, где 
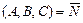- нормальный вектор плоскости;
2) 
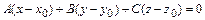- уравнение плоскости, проходящей через точку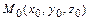 
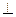вектору 
;
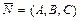3) 
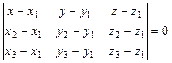- уравнение плоскости, проходящей через три точки 
, 
и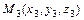 
;
4) 
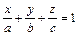-уравнение плоскости в отрезках, где , 
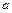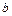и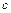 
- дины отрезков (со знаком 
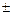), отсекаемых плоскостью на осях , 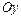и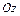 
(«
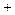», если на положительной части оси и «
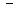», если на отрицательной).
Если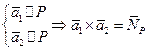 
.
Расстояние от точки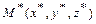 
до плоскости 
: 
.
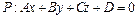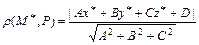Угол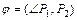 
, (
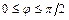) между плоскостям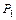и 
и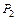 
: 
.
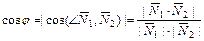, если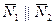 
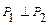, если 
.
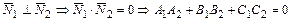Date: 2015-04-23; view: 393; Нарушение авторских прав