Примеры решения задач. · Энергия заряженного проводника выражается через заряд Q, потенциал φ и электрическую емкость С проводника следующими соотношениями:

ЭНЕРГИЯ ЗАРЯЖЕННОГО ПPOBOДHИКA.

ЭHEPГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Основные формулы

· Энергия заряженного проводника выражается через заряд Q, потенциал φ и электрическую емкость С проводника следующими соотношениями:

· Энергия заряженного конденсатора

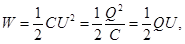
где С - электрическая емкость конденсатора; U - разность по­тенциалов на его пластинах.

· Объемная плотность энергии (энергия электрического поля, приходящаяся на единицу объема)

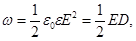
где Е - напряженность электрического поля в среде с диэлектрической проницаемостью ε; D - электрическое смещение.

Примеры решения задач

Пример 1. Конденсатор электроемкостью C₁=З мкФ был заря­жен до разности потенциалов U ₁ =40 В. После отключения oт источника тока конденсатор был соединен параллельно с другим незаря­женным конденсатором электроемкостью С ₂ = 5 мкФ. Определить энергию Δ W, израсходованную на образование искры в момент присоединения второго конденсатора.

Р е ш е н и е. Энергия, израсходованная на выбрасывание искры, равна

Δ W = W ₁- W ₂ (1)

где W ₁ - энергия, которой обладал первый конденсатор до, присо­единения к нему второго конденсатора; W ₂ - энергия, которую имеет батарея, составленная из первого и второго конденсаторов. Подставив в равенство (1) формулу энергии заряженного конденсатора

W=CU ²/2 и приняв во внимание, что общая электроемкость параллельно соеди­ненных конденсаторов равна сумме электроем­костей отдельных конденсаторов, получим

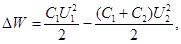(2)

где С ₁ и С ₂ - электроемкости первого и второго конденсаторов; U ₁- разность по­тенциалов, до которой был заряжен первый кон­денсатор; U ₂ - разность потенциа­лов на зажимах батареи конден­саторов.

Учитывая, что заряд после присоединения второго конденсатора остался преж­ним, выразим разность потенциалов U ₂ следующим образом: Подставив это выражение U ₂ в формулу (2), полу­чим

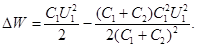
После простых преобразований найдем

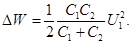
Выполнив вычисления, получим Δ W= 1,5 мДж.

Пример 2. Плоский воздушный конденсатор с площадью S пла­стины, равной 500 см², подключен к источнику тока, ЭДС которого равна 300 В. Определить работу А внешних сил по раз­движению пластин от расстояния d ₁ = 1 см до d ₂ = 3 см в двух слу­чаях: 1) пластины перед раздвижением отключаются от источника тока; 2) пластины в процессе раздвижения остаются подключенны­ми к нему.

Р е ш е н и е. l-й случай. Систему двух заряженных и отклю­ченных от источника тока пластин можно рассматривать как изоли­рованную систему, по отношению к которой справедлив закон сохранения энергии. В этом случае работа внешних сил равна измене­нию энергии системы:

A= Δ W=W ₂ -W ₁, (1)

где W ₂ - энергия поля конденсатора в конечном состоянии (пласти­ны находятся на расстоянии d ₂ ); W ₁ - энергия поля в начальном состоянии (пластины находятся на расстоянии d ₁).

Энергию в данном случае удобно выразить через заряд Q на пластинах, так как заряд пластин, отключенных от источника при их раздвижении, не изменяется. Подставив в равенство (1) выраже­ния W ₂ =Q ² / (2С₂) и W ₁ =Q ² /(2С ₁), полу­чим

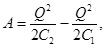ИЛИ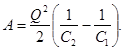

Выразив в этой формуле за­ряд через ЭДС ε источника тока и начальную электроемкость С ₁ (Q=C ₁ ε), най­дем

(2)

Подставляя в формулу (2) выражения электроемкостей (C ₁ =ε ₀ S/d ₁ и C ₂ = =ε ₀ S/d ₂ ) плоского конденсатора, получим

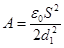ε ²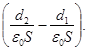

После сокращения на ε₀ S формула примет вид

A= ε₀ Sε² (d ₂ -d ₁) / 2d ₁² (3)

Произведя вычисления по формуле (3), найдем A= 3,98 мкДж.

2-й случай. Пластины остаются подключенными к источнику тока и система двух пластин уже не является изолированной (заряд с пластин при их раздвижении перемещается к клеммам батареи). Поэтому воспользоваться законом сохранения энергии в этом слу­чае нельзя.

Заметим, что при раздвижении пластин конденсатора: а) разность их потенциалов остается неизменной (U=ε); б) емкость бу­дет уменьшаться (С = ε₀S/ d.) Будут уменьшаться также заряд на пластинах (Q=CU) и напряженность электрического поля (Е = U/d). Так как величины Е и Q, необходимые для определения работы, изменяются, то работу следует вычислять путем интегрирования.

Напишем выражение для элементарной работы:

d A=QE ₁dx, (4)

где E ₁ - напряженность поля, создаваемого зарядом одной пласти­ны.

Выразим напряженность поля E ₁ и заряд Q через расстояние х между пластинами:

E ₁ = 1/2 Е = ε/2х и Q = Cε, или Q = ε₀S ε / x.

Подставив эти выражения E ₁ и Q в равенство (4), получим

d A= 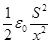ε ²d x.

Проинтегрировав это равенство в пределах от d ₁ до d ₂, найдем выражение искомой работы:

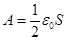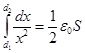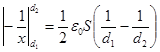ε ε ² ε ².

После упрощений последняя формула примет вид

A= ε₀S ε ²(d₂-d₁)/(2d₁d₂)

Сделав вычисления по полученной формуле, найдем

А= 1.33 мкДж.

Пример, 3. Плоский конденсатор заряжен до разности потенциалов U = 1 кВ. Расстояние d между пластинами равно 1 см. ДИЭ;/1ект­рик - стекло. Определить объемную плотность энергии поля кон­денсатора.

Р е ш е н и е. Объемная плотность энергии поля конденсатора

ω =W/V, (1)

где W - энергия поля конденсатора; V- объем, занимаемый по­лем, т. е. объем пространства, заключенного между пластинами конденсатора.

Энергия поля конденсатора определяется по формуле

W=CU ² / 2, (2)

где U - разность потенциалов, до которой заряжены пластины конденсатора; С - его электроемкость. Но C=εε ₀ S / d, V=Sd. Подставив выражение С в формулу (2) и затем выражения W и V в формулу (1), получим

ω= εε₀ U ² / (2 d ²).

Подставив значения величин в последнюю формулу и вычислив, найдем

ω =0,309 Дж/м³.

Пример 4. Металлический шар радиусом R= 3 cм несет заряд Q =20 нКл. Шар окружен слоем парафина толщиной d= 2см. Определить энергию W электрического поля, заключенного в слое ди­электрика.

Р е ш е н и е. Так как поле, созданное заряженным шаром, яв­ляется неоднородным, то энергия поля в слое диэлектрика распределена неравномерно. Однако объемная плотность энергии будет одинакова во всех точках, отстоящих на равных рас­стояниях от центра сферы так как поле заряженного шара обладает сферической симметрией.

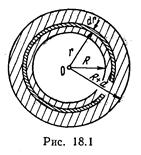Выразим энергию в элементарном сфе­рическом слое диэлектрика объемом dV: d W= ω d V, где ω - объемная плотность энергии (рис. 18.1).

Полная энергия выразится интегралом

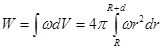, (1)

где r- радиус элементарного сферического слоя; d r- его толщи­на. Объемная плотность энергии определяется по формуле ω =εε ₀ Е²/2, где Е- напряженность поля. В нашем случае и, следовательно,

Подставив это выражение плотности в формулу (1) и вынеся за знак интеграла постоянные величины, получим

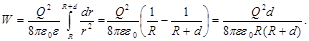
произведя вычисления по этой формуле, найдем

W= 12 мкДж.

Задачи

Энергия плоского конденсатора

18.1. Конденсатору, электроемкость С которого равна 10 пФ, сообщен заряд Q= 1 пКл. Определить энергию W конденсатора.

18.2. Расстояние d между пластинами плоского конденсатора равно 2 см, разность потенциалов U= 6 кВ. Заряд Q каждой пласти­ны равен 10 нКл. Вычислить энергию W поля конденсатора и силу F взаимного притяжения пластин.

18.3. Какое количество теплоты Q выделится при разряде плоского конденсатора, если разность потенциалов U между пластинами равна 15 кВ, расстояние d= 1 мм, диэлектрик - слюда и площадь S каждой пластины равна 300 см²?

18.4. Сила F притяжения между пластинами плоского воздушного конденсатора равна 50 мН. Площадь S каждой пластины равна 200 см². Найти плотность энергии ω поля конденсатора.

18.5. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r = 10 см каждая. Расстояние d ₁ между пластинами равно 1см. Конденсатор зарядили до разности потенциалов U =1,2 кВ и отключили от источника тока. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d ₂=3,5 см?

18.6. Плоский воздушный конденсатор электроемкостью С =1,11 нФ заряжен до разнести потенциалов U = 300 В. После отключения от источника тока расстояние между пластинами конденсатора было увеличено в пять раз. Определить: l) разность потен­циалов U на обкладках конденсатора после их раздвижения; 2) ра­боту А 'внешних сил по раздвижению пластин.

18.7. Конденсатор электроемкостью С ₁=666 пФ зарядили до разности потенциалов U = 1,5 кВ и отключили от источника тока. 3атем к конденсатору присоединили параллельно второй, незаря­женный конденсатор электроемкостью С ₂ =444 пФ. Определить энергию, израсходованную на образование искры, проскочившей при соединении конденсаторов.

18.8. Конденсаторы электроемкостями С ₁ = 1 мкФ, С ₂ = 2 мкФ, С₃=3 мкФ включены в цепь с напряжением U = 1,1 кВ. Определить энергию каждого конденсатора в случаях: 1) последовательного их включения; 2) параллельного включения.

18.9. Электроемкость С плоского конденсатора равна 111 пФ.

Диэлектрик - фарфор. Конденсатор зарядили до разности потен­циалов U=600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденса­тора? Трение пренебрежимо мало.

18.10. Пространство между пластинами плоского конденсатора заполнено диэлектриком (фарфор), объем V которого равен 100 см³. Поверхностная плотность заряда σ на пластинах конденсатора рав­на 8,85 нКл/м². Вычислить работу А, которую необходимо совер­шить для того, чтобы удалить диэлектрик из конденсатора. Трени­ем пренебречь.

18.11. Пластину из эбонита толщиной d= 2 мм и площадью S= 300 см² поместили в однородное электрическое поле напряжен­ностью Е= 1 кВ/м, расположив так, что силовые линии перпендику­лярны ее плоской поверхности. Найти: 1) плотность σ связанных зарядов на поверхности пластин; 2) энергию W электрического поля, сосредоточенную в пластине.

18.12. Пластину предыдущей задачи переместили из поля в об­ласть пространства, где внешнее поле отсутствует. Пренебрегая уменьшением поля в диэлектрике с течением времени, определить ­энергию W электрического поля в пластине.

Энергия поля заряженной сферы

18.13. Найти энергию W уединенной сферы радиусом R= 4 см, заряженной до потенциала φ=500 В.

18.14. Вычислить энергию W электростатического поля металлического шара, которому сообщен заряд Q =100 нКл, если диаметр d шара равен 20 см.

18.15. Уединенная металлическая сфера электроемкостью С = 10 пФ заряжена до потенциала φ=3 кВ. Определить энергию W поля, заключенного в сферическом слое, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в три раза больше радиуса сферы.

18.I6. Электрическое поле создано заряженной (Q= 0,1 мкКл) сферой радиусом R= 10 см. Какова энергия W поля, заключенная в объеме, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в два раза больше радиуса сферы?

18.17. Уединенный металлический шар радиусом R ₁ = 6 см несет заряд Q. Концентрическая этому шару поверхность делит простран­ство на две части (внутренняя конечная и внешняя бесконечная), так что энергии электрического поля обеих частей одинаковы. Определить радиус R ₂ этой сферической поверхности.

18.18. Сплошной парафиновый шар радиусом R= 10 см заряжен равномерно по объему с объемной плотностью ρ= 10 нКл/м³. Опре­делить энергию W ₁ электрического поля, сосредоточенную в самом шаре, и энергию W ₂ вне его.

18.19. Эбонитовый шар равномерно заряжен по объему. Во сколько раз энергия электрического поля вне шара превосходит энергию поля, сосредоточенную в шаре?

Date: 2015-05-23; view: 3579; Нарушение авторских прав