И структуры

Во многих случаях имеется необходимость на одной и той же координатной диаграмме отразить не одну, а несколько линий, характеризующих динамику различных абсолютных или относительных показателей либо однородного, либо неоднородного характера.

Если изображаемые на диаграмме показатели имеют однородный характер (например, динамика урожайности отдельных видов зерновых культур), то их отражают в исходных единицах измерения. При этом каждую линию, характеризующую динамику отдельного вида культур, целесообразно расшифровать. Для этого достаточно обозначить наименование показателя с правой стороны диаграммы, против соответствующей линии. Примером такого способа графического изображения является комбинированная линейная диаграмма динамики урожайности озимых и яровых культур в сельскохозяйственной организации (рис. 5.2).

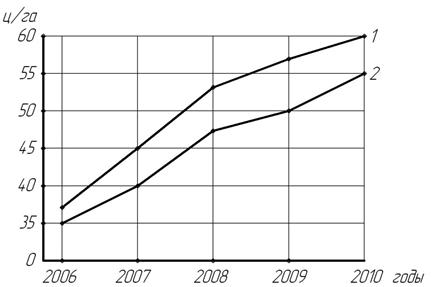
Рис. 5.2. Динамика урожайности озимых и яровых культур (линейная диаграмма):

1 – озимые; 2 – яровые

Нередки случаи, когда необходимо графически изобразить динамику нескольких неоднородных показателей на одной и той же линейной диаграмме. При этом целесообразно прежде всего абсолютные показатели динамики превратить в относительные величины, например, рассчитать базисные коэффициенты роста по каждому абсолютному показателю. Затем их размещают в системе координат, что позволяет наглядно проследить развитие динамики не только по каждому показателю в отдельности, но и сравнить динамику всех изображаемых неоднородных показателей (рис. 5.3).

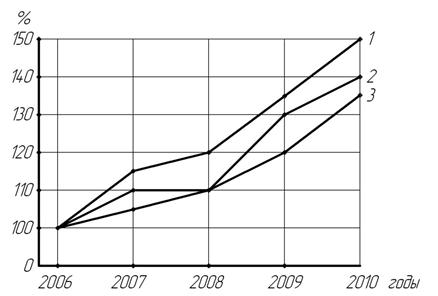
Рис. 5.3. Динамика экспорта молочной продукции на молочном комбинате (линейная диаграмма): 1 – масло; 2 – сыры; 3 – казеин

При графическом изображении структуры сложных признаков могут быть применены секторные, квадратно-сетчатые, слоистые и др. виды диаграмм.

Секторная диаграмма – довольно распространенная форма наглядного сопоставления различных частей единого целого при помощи площадей, образуемых секторами круга. Она строится путем разделения круга на секторы пропорционального удельному весу частей в составе сложного признака. Размер каждого сектора определяется величиной угла из расчёта, что 1 % соответствует 3,6°. Во всех секторных диаграммах, независимо от величины круга, масштаб графика всегда постоянен, т.е. М: 1 % = 3,6°. Чтобы легче различать секторы, целесообразно пользоваться приёмом различной штриховки или цветной раскраски для каждого сектора (рис. 5.4).

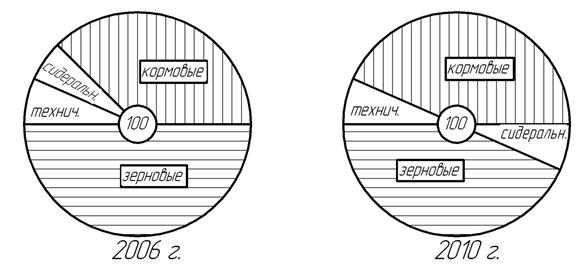
Рис. 5.4. Структура посевных площадей в сельскохозяйственной организации «Днепр» (секторная диаграмма)

Секторные диаграммы обычно используются в тех случаях, когда необходимо графически изобразить структуру сложного показателя, например, за сравнительно небольшое число (2–3) промежутков или моментов времени, а также по небольшому числу однородных единиц или объектов.

Если же структурные показатели требуется изобразить в длительной динамике (например, за 5 -–10 периодов), то в этом случае предпочтительнее воспользоваться способом слоистых диаграмм. Сущность его заключается в том, что на прямой горизонтальной линии размещают равные по основанию и высоте и одинаково отстоящие друг от друга столбики. Принимается условие, что каждый столбик – это общий (итоговый) структурный показатель за отдельный промежуток времени (например, за декаду, месяц, квартал, год и т.д.). Столбики по высоте делят на 100 равных частей, где каждая часть соответствует I %, Следовательно, на диаграмме высота каждой составной части пропорциональна ее удельному весу в составе всего сложного признака. Затем идентичные линии по каждой составной части во всех столбиках с помощью лекала соединяют, в результате чего за весь изучаемый период получаются слои, наглядно показывающие динамику удельных весов в составе сложного признака. Пример слоистой диаграммы представлен на рис. 5.5.

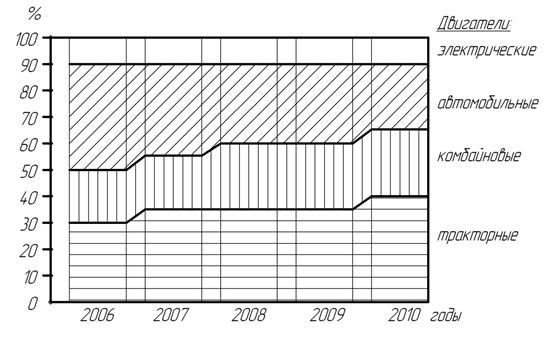
Рис. 5.5. Структура энергетических мощностей в сельскохозяйственной организации «Днепр» (слоистая диаграмма)

Квадратно-сетчатые диаграммы – это равные квадраты, разделенные на 100 одинаковых частей (квадратиков), полученных путем пересекающихся перпендикулярных линий. Это означает, что каждый квадратик равен 1/100 всей площади квадрата, т.е. I % объема сложного признака. Зная удельный вес каждой его составной части, нетрудно определить, сколько квадратиков может она занимать.

Квадратно-сетчатые диаграммы аналогично секторным могут быть использованы при графическом изображении структуры сложных признаков за сравнительно небольшое число периодов иди моментов времени, а также по небольшому количеству статистических единиц или объектов (рис. 5.6).

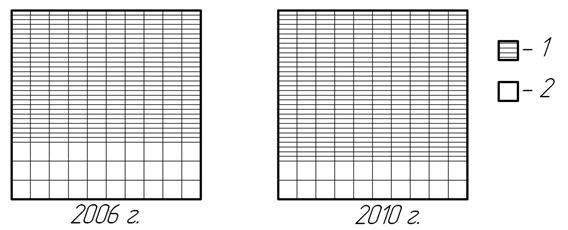
Рис. 5.6. Структура землепользования в сельскохозяйственной организации «Днепр» (квадратно-сетчатая диаграмма): 1 – с.-х. земли; 2 – не с.-х. земли

Date: 2015-05-23; view: 507; Нарушение авторских прав