
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Оценки показателей каждым из опрошенных экспертов
|
|
| Показатели | Эксперты | |||||||||
| е1 | ||||||||||
| е2 | ||||||||||
| е3 | ||||||||||
| е4 | ||||||||||
| е5 | ||||||||||
| е6 |
Задача состоит в выборе наиболее значимого элемента еi или группы этих элементов при разных предположениях относительно требований к точности совпадения мнений всех экспертов.
E={ еi } i=1,6
К=К1 К2…..К10
Оценки рассматриваемых показателей каждым из опрашиваемых экспертов
αКj , i = 1,2…6 К = 1,2….10 совпадают с данными таблицы 1.1.
Теперь построим матрицу соответствия.
С этой целью для каждой пары объектов (еi,еj) определим коэффициенты соответствия сij, исходя из предположения, что объект еi предпочтительнее еj..
Результаты расчётов представлены следующей матрицей С
| еj | еi | |||||||
| е1 | е2 | е3 | е4 | е5 | е6 | |||
 е1 е1
| С12 = 0,6 | 0,8 | 0,5 | 0,5 | 0,6 | |||
 е2 е2
| 0,4 | 0,4 | 0,4 | 0,3 | 0,3 | |||
 е3 е3
| 0,2 | 0,5 | 0,3 | 0,1 | 0,2 | |||
 е4 е4
| 0,5 | 0,4 | 0,4 | 0,5 | 0,4 | |||
 е5 е5
| 0,7 | 0,7 | 1,0 | 0,8 | 0,8 | |||
 е6 е6
| 0,4 | 0,7 | 0,9 | 0,6 | 0,3 |
Расчет к-та С12
Выдвигаем гипотезу, что е1 предпочтительнее е2. Это предположение разделяют экспертов. Множество критериев, соответствующих этому предположению, С12 имеют номера: К = 2,3,4,5,6,9. Следовательно
С12 = 
Аналогично рассчитываются значения остальных элементов матрицы С.
После построения матрицы соответствия С нужно рассчитать значение элементов матрицы несоответствия Д.
Элемент матрицы несоответствия Д учитывает те критерии, по которым существует противоречие вынесенной гипотезе, что объект е1 предпочтительнее объекта е2. Для расчёта необходимо:
Для пары объектов (еi,еj) показатель dij (1) рассчитывается следующим образом:
1. Выделяется множество экспертов, оценки которых противоречат выдвинутой гипотезе, что объект е1 предпочтительнее объекта е2. К = 1,7,8,10
2. Для этих критериев рассчитаем разность оценок объектов е1 и е2 – величину несоответствия.
[α12 - α1 1] = 2
[α72 - α7 1] = 3
[α82 - α8 1] = 3
[α102 - α10 1] = 4
Полученные величины упорядочиваются в порядке невозрастания: [4,3,3,2]
3. Показатель несоответствия d12 (1) = 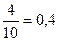 вычисляется как отношение первого члена последовательности из п.2 к масштабу шкалы. Соответственно при s = 2 d12 (2) =
вычисляется как отношение первого члена последовательности из п.2 к масштабу шкалы. Соответственно при s = 2 d12 (2) = 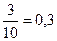
Матрица Д (1)имеет вид
| еi | |||||
| е1 | е2 | е3 | е4 | е5 | е6 | |
 е1 е1
| d12 (1) = 0,4 | 0,6 | 0,5 | 0,2 | 0,6 | |
 е2 е2
| 0,4 | 0,4 | 0,3 | 0,4 | 0,2 | |
 е3 е3
| 0,7 | 0,5 | 0,6 | |||
 е4 е4
| 0,5 | 0,5 | 0,5 | 0,5 | 0,5 | |
 е5 е5
| 0,9 | 0,7 | 0,7 | 0,8 | 0,6 | |
 е6 е6
| 0,8 | 0,6 | 0,5 | 0,7 | 0,2 |
Данные матриц С и Д (s) позволяют построить графы сравнения объектов при различных требованиях к порогам соответствия и несоответствия и выделить ядро соответствующего графа.
Рассмотрим, как изменяются графы в зависимости от значения параметров (c, d, s).
Пусть s = 1, С = 0,8, d = 0,3. Тогда можно провести сравнение только для двух объектов - е3 и е5.
Ядро графа включает пять элементов í е1 е2 е4 е5 е6 ý.
Другими словами, эти объекты при указанных требованиях к совпадению мнений экспертов не сравнимы между собой. При этом объект е5 признаётся более значимым, чем объект (показатель) е3.
Снижение требований к порогу соответствия С = 0,7 приводит к дополнительной возможности сравнения показателей е1 и е5. (рис б). Следовательно, ядро этого графа содержит теперь элементы íе2 е4 е5 е6 ý.
При s = 2 и тех же порогах соответствия и несоответствия (С = 0,8, d = 0,3) граф содержит единственный элемент (показатель), превосходящий все остальные. Таким образом, показатель е5 может быть принят в качестве основного при решении данной проблемы с указанной степенью риска, отраженной набором оценок степени согласованности мнений экспертов.
Точно так же введение более строгих требований к порогу несоответствия (уменьшение значения d с 0,3 до0,2) приводит к введению в ядро графа элемента е6 (рис. е). Исследование изменений ядер графов в зависимости от изменения требований к параметрам согласования различных критериев (различных мнений экспертов) позволяет упорядочить рассматриваемые объекты.
Выбрать лучшие объекты (показатели) на основе построения ядра графа
Вариант 1
Date: 2015-05-23; view: 733; Нарушение авторских прав