Метод переменных состояния

Факультет автоматики и электромеханики

Кафедра теоретической и общей электротехники

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

(Метод переменных состояния)

Методические указания к выполнению курсовой работы

Составил Башев А.А.

Ред. проф. Алтунин Б.Ю.

Н.Новгород, 2010

Метод переменных состояния.

В основу метода переменных состояния положена принципиальная возможность замены дифференциального уравнения n -го порядка электрической цепи n дифференциальными уравнениями первого порядка. В качестве переменных состояния принимают токи индуктивностей 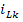и напряжения на ёмкостях 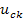, которые однозначно определяют запас энергии цепи в любой момент времени. Систему уравнений состояния можно представить в виде матричного уравнения:

,

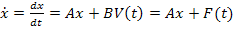где: 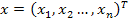– столбцевая матрица (вектор) n переменных состояния;

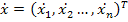– столбцевая матрица (вектор) n первых производных переменных состояния;

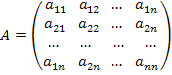- квадратная матрица размером 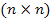, элементы которой определяются коэффициентами дифференциального уравнения цепи;

V(t) – столбцовая матрица (вектор) m независимых воздействий;

B – матрица размером 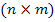, элементы которой зависят от параметров цепи и её структуры;

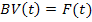– столбцовая матрица, элементы которой зависят от независимых воздействий, структуры и параметров цепи.

Формирование системы дифференциальных уравнений цепи основано на использовании дифференциальных уравнений для переменных состояния, согласно которым

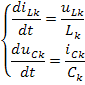
Расчёт цепей методом переменных состояний можно разделить на два этапа:

1) На первом этапе составляют систему дифференциальных уравнений цепи;

2) На втором этапе решают составленную систему дифференциальных уравнений;

Решение системы дифференциальных уравнений, составленных методом переменных состояния, можно выполнить двумя способами: аналитическим и численным.

При аналитическом способе решение уравнений состояния записывают в виде суммы матриц принуждённой 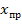и свободной 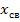составляющих:

;

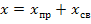где: 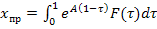– соответствует реакции цепи от внешних воздействий 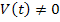при нулевых начальных условиях ;

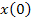– матрица (вектор) начальных значений переменных состояния, полученных при ;

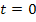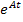– матричная экспоненциальная функция.

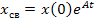– соответствует реакции цепи, обусловленной ненулевыми начальными условиями 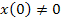; при отсутствии внешних воздействий V=0;

Если в цепи после коммутации нет источников энергии, т.е. 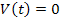, то решение матричного уравнения имеет вид:

.

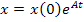Если же после коммутации есть источники независимых воздействий, то матрица 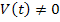, и интегрирование матричного уравнения 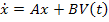приводит к решению в виде:

,

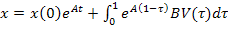которое состоит из суммы двух слагаемых – реакции цепи при ненулевых начальных условиях и реакции цепи при нулевых начальных условиях и наличии источников внешних воздействий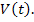

При численном способе решения уравнений состояния используют различные программы численного интегрирования на ЭВМ: метод Рунге-Кутта, метод Эйлера, метод трапеций и др. Так, например, в пакете программ MathCAD приведены программы численного решения дифференциальных уравнений модифицированном методом Эйлера и методом Рунге-Кутта. Поскольку погрешность решения методом Эйлера достигает нескольких процентов, то более предпочтительным является метод Рунге-Кутта, который при решении уравнений четвёртого порядка даёт погрешность 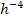, где 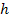– шаг приращения переменной. Этот метод обеспечивает контроль точности вычислений на каждом шаге интегрирования и программную регулировку шага.

В системе MatchCAD программа интегрирования уравнений по методу Рунге-Кутта имеет имя rkfixed. Обращение к ней производится через операцию присваивания какой-либо переменной (в дальнейшем z) имени программы:

,

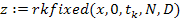где: x – вектор переменных состояния, размер которого определяется вектором начальных значений 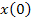и соответствует числу уравнений состояния;

0 и 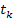– начало и конец временного интервала интегрирования;

N – число точек на интервале интегрирования;

D – функция, которая описывает правую часть уравнений, разрешённых относительно первых производных.

Для линейных цепей функция D имеет вид линейного матричного преобразования 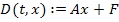, где A – квадратная матрица коэффициентов, которые определяются структурой цепи и параметрами элементов; F – вектор независимых переменных, элементы которого определяются входными воздействиями. Все элементы матриц A и F должны быть определенны перед обращением к программе rkfixed.

Матрица z имеет размер 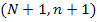, где первый столбец (нулевой) соответсвует дискретным значениям времени 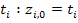. Остальные столбцы этой матрицы соответствуют значениям переменных состояния: 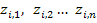, где индекс i изменяется от 1 до N.

Для контоля правильности задания исходных данных можно (но не обязательно) обратиться к программе определения собственных чисел матрицы A: eigenvals (A). Эта программа выводит информацию о собственных числах, которые совпадают с корнями характеристического уравнения цепи. Необходимым, но недостаточным условием правильности ввода данных, является набор отрицательных собственных чисел (или комплексно-сопряжённых чисел с отрицательно вещественной частью).

Рассмотрим теперь некоторые способы составления дифференциальных уравнений цепи по методу переменных состояния. Для этих целей наиболее часто применяют два основных способа:

1) использование законов Кирхгофа;

2) использование метода наложения.

Рассмотрим применение этих способов на некоторых примерах.

Пример 1. Требуется составить уравнения состояния и решить их для одноконтурной цепи второго порядка при отключении источника напряжения Е. Схема цепи приведена на рисунке 1(а), а параметры её элементов имеют следующие значения: Е=40 В; r=40 Ом; L=1 Гн; С=500мкФ.

Решение. Посмотрим схему замещения цепи для произвольного момента времени t, которая приведена на рисунке 1(б). На этой схеме ёмкость С заменена источником постоянного напряжения 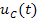, а индуктивность L – источником тока 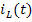. Результирующая схема замещения содержит только сопротивление r, источник тока 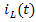и источник напряжения .

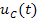а) б)

Рисунок 1. Исходная (а) и расчётная (б) схемы цепи к примеру 1.

Для полученной схемы можно составить уравнения, пользуясь законами Кирхгофа:

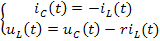
Откуда находим:

,

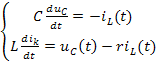Из этих уравнений получаем значение первых производных переменных состояния:

.

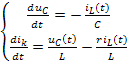Пользуясь которыми, запишем матричное уравнение цепи:

,

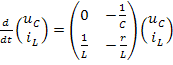При использовании программы rkfixed это уравнение записывают в виде:

,

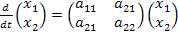где .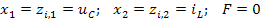

Это матричное уравнение необходимо ещё дополнить матрицей начальных состояний цепи, которая включает напряжение на ёмкости и ток в индуктивности на момент коммутации (т.е. при t=0_):

,

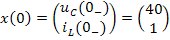используемой для начала процесса интегрирования дифференциальных уравнений цепи.

Перед обращением к программе интегрирования rkfixed определяем через операцию присваивания значения следующих величин:

1) коэффициентов матрицы А: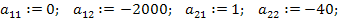

2) значений вектора начальных состояний переменных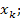

3) число точек интегрирования ;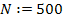

4) формализованную матричную запись уравнений состояния 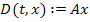при условии, что F=0;

5) конечное значение временного интервала .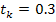

Необходимый временной интервал интегрирования 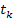можно оценить по собственным числам матрицы А путём обращения к программе eigenvals (А). В рассматриваемом примере имеются два комплексно сопряжённых числа 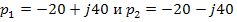, вещественные части которых одинаковы и равны 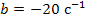. Эта часть комплексного числа определяет коэффициент затухания и непосредственно связана с длительностью переходного процесса формулой 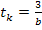. Для наглядности в рассматриваемом примере интервал интегрирования выбран в два раза больше .

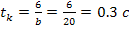Форма записи исходных данных для программы rkfixed и результаты расчёта приведены на рисунке 2. Поскольку переменные состояния 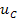и 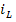измеряются в разных единицах и могут значительно отличаться друг от друга, то при построении графиков необходимо указать масштабные коэффициенты. Так, например, для графика переменной 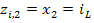использован масштабный коэффициент, равный 100. Чтобы получить действительное значение тока 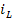, следует разделить значения, отсчитываемые по оси ординат, на 100.

Из полученных графиков следует, что переходный процесс в цепи носит колебательных характер, а обе функции постепенно затухают до нулевого значения при увеличении времени t.

Рисунок 2. Результаты расчёта к примеру 1.

Пример 2. Составить уравнения для переменных состояния и рассчитать их при замыкании ключа К в цепи второго порядка, изображённой на рисунке 3(а). Параметры элементов цепи имеют следующие значения: А; r₁=r₂=50 Ом; L=5 мГн; С=0,1 мкФ.

Решение. Переходный процесс в рассматриваемой цепи возникает в результате перераспределения энергии между индуктивностью L и ёмкостью C после подключения сопротивления r₁. Используя первый закон Кирхгофа, определим ток в ёмкости С:

.

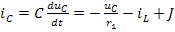а) б)

Рисунок 3. Исходная (а) и расчётная (б) схемы к примеру 2.

Аналогично, используя второй закон Кирхгофа, найдём напряжение на индуктивности:

.

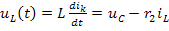Объединим эти уравнения в систему для переменных состояния:

.

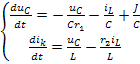Полученную систему уравнений запишем в матричной форме:

.

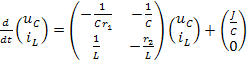После подстановки числовых значений параметров элементов получим уравнения состояния в виде:

.

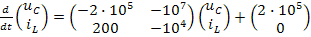Для определения вектора начальных значений найдём напряжение на ёмкости и ток в индуктивности до замыкания ключа К:

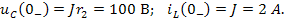
Таким образом, вектор начальных значений переменных состояния имеет вид:

.

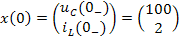Схемы замещения для расчёта значений переменных состояния приведена на рисунке 3(б). На этой схеме ёмкость заменена источником напряжения 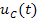, а индуктивность – источником тока 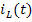. Значения этих величин изменяются на каждом шаге интегрирования.

Решение уравнений состояния выполним по программе rkfixed, входящей в систему MathCAD. Для этого присвоим переменным состояния следующие значения: 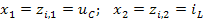и запишем уравнения состояния в виде:

,

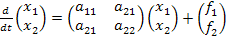где значения коэффициентов можно взять из уравнений состояния, рассчитанных выше, и включить в программу констант или определить через операции присваивания в самой программе.

Форма задания исходных данных для расчёта по программе rkfixed приведена на рисунке 4. Значение N=5000 указано произвольно, так как оно влияет только на время выполнения расчёта и точность. Косвенно оценить точность расчёта можно, сравнив результаты интегрирования для двух значений N=N₁ и N₁/2. Если результаты расчета в этих точках совпадают, то точность вычислений и число точек интегрирования на интервале t_k находится в приемлемых пределах.

Через операцию присваивания определяем также вектор начальных значений х и вектор независимых источников F. Временной интервал t_k может быть указан произвольно или приближённо выбран с помощью анализа чисел матрицы А.

Для апериодического процесса, который существует в рассматриваемой цепи, следует выбрать наименьшее по модулю собственное число p_min и воспользоваться формулой t_k =3/ p_min. Из двух собственных чисел p₁ =-1.888E5 1/c; p₂ =-2.118E4 1/c меньшее значение имеет p₂, поэтому t_k =3/2,118Е4=1,42Е-4 с.

Выбор интервала t_k можно также выполнить, анализируя постоянные времени цепей первого порядка, которые можно построить на основе исходной цепи путём последовательного исключения реактивных элементов. При этом из найденных постоянных времени следует выбрать ту, которая имеет максимальное значение, и, используя её, рассчитать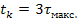

Графики временных зависимосте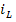й и 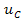приведены на рисунке 4. Для переменной использован масштабный коэффициент, равный 100. Из этих графиков видно, что напряжение на ёмкости изменяется от 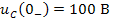до уровня 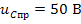, а ток в индуктивности – от до .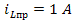

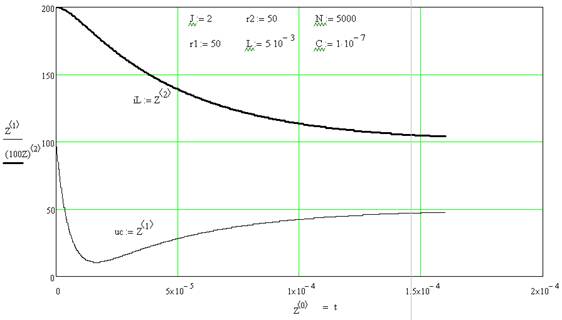
Рисунок 4. Результаты расчёта к примеру 2.

Пример 3. Составить уравнения для переменных состояния и выполнить расчёт переходного процесса в цепи третьего порядка, приведённой на рисунке 5(а) при замыкании ключа К. Параметры элементов цепи имеют следующие значения: Е=120 В; r₁=r₃=r₄=1 Ом; r₂=r₅=2 Ом; L₁=1 мГн; L₂=2 мГн; С=10 мкФ.

а) б)

Рисунок 5. Исходная (а) и расчётная (б) схемы к примеру 3.

Решение. Переходный процесс в схеме обусловлен перераспределением энергии реактивными элементами цепи после коммутации ключа К. На рисунке 5(б) изображена схема замещения цепи, на которой реактивные элементы заменены источниками напряжения и тока. Положительные направления этих источников согласованы с исходной схемой. При расчёте схемы замещения определению подлежат напряжения на источниках тока 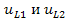, и ток в ёмкости 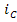, так как именно они определяют производные от переменных состояния. При расчёте этих величин воспользуемся принципом наложения, в соответствие с которым реакцию линейной цепи можно определить в виде суммы реакций от отдельных источников. Для этого рассмотрим четыре частные схемы, приведённые на рисунке 6, в каждой из которых действует только один из источников, входящих в схему, приведённую на рисунке 5(б).

Расчёт схемы, приведённой на рисунке 6(а), позволяет определить искомые величины от действия источника напряжения :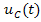

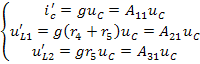; где .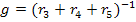

Аналогично выполняется расчёт схемы, изображённой на рисунке 6(б), пользуясь которой, определим те же величины от действия источника тока :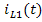

а) б)

в) г)

Рисунок 6. Схемы для расчёта цепи от напряжения 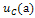, тока 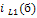, тока , источника Е (г) к примеру 2.

;

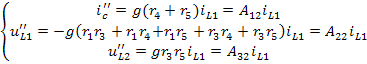Выполнив расчёт схемы, приведённой на рисунке 6(в), найдём искомые величины при действии :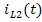

.

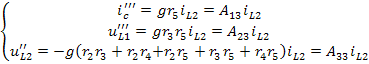Расчёт схемы, изображённой на рисунке 6(г), позволяет определить искомые величины от действия напряжения Е:

.

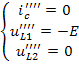Суммируя частные решения для отдельных источников с учётом выбранных положительных направлений напряжений и токов, находим полные значения искомых величин:

.

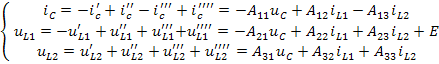Полученные уравнения позволяют сформулировать нормальную систему дифференциальных уравнений для переменных состояния и записать её в матричной форме:

,

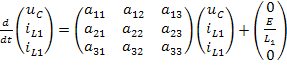где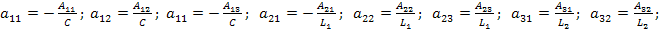

.

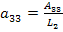После подстановки значений параметров элементов цепи найдём числовые значения коэффициентов уравнений:

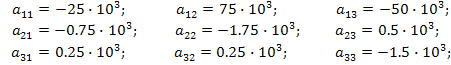
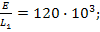
К системе уравнений, записанной в нормальной форме, необходимо добавить вектор, который отражает начальное состояние цепи в момент .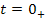

Так как переменные состояния подчиняются законам коммутации, то этот вектор можно получить из анализа состояния цепи до коммутации, т.е. при :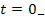

.

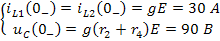Таким образом, вектор начальных состояний цепи имеет вид:

.

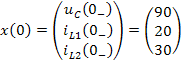При обращении к программе rkfixed, входящей в систему MathCAD, можно использовать найденные выше значения коэффициентов дифференциальных уравнений или задать их в виде расчётных формул с указанием значений исходных параметров схемы. На рисунке 7 приведён результат расчёта по программе rkfixed. При построении графиков приняты следующие обозначения и масштабные коэффициенты: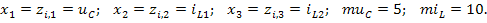

Рисунок 7. Результаты к примеру 3.

Кроме этого, при вводе данных указано время интегрирования, которое, как и раньше, выбрано по формуле t_k =3/ b_min, где b_min – минимальное значение модуля вещественной части собственных чисел матрицы eigenvals (A). Для рассматриваемого примера это число имеет значение b =1.268E3, откуда находим значение t_k =2E-3 с.

Date: 2015-05-22; view: 6051; Нарушение авторских прав