Деревья

Рассмотрим деревья – наиболее важные нелинейные структуры, которые встречаются при работе с компьютерными алгоритмами.

Формально дерево определяется как конечное множество Т одного или более узлов со следующими свойствами:

1. существует один выделенный узел, а именно – корень данного дерева Т;

2. остальные узлы (за исключением корня) распределены среди m0 непересекающихся множеств Т1, …, Тm и каждое из этих множеств в свою очередь, является деревом; деревья Т1, …, Тm называются поддеревом данного корня.

Как видно из определения, оно является рекурсивным, и тем самым отражает рекурсивное свойство всех древовидных структур.

Способы представления дерева

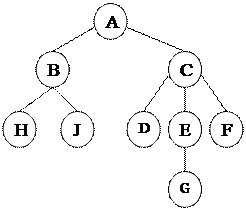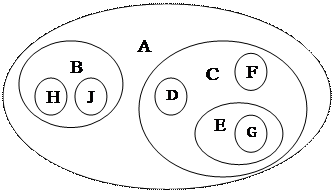a) b)

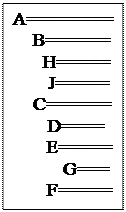
с) (A (B (H) (J)) (C (D) (E(G)) (F)))

d)

Рис. 7.2 Способы изображения древовидных структур: а) обычная схема дерева; b) вложенные множества; c) список с отступами; d) вложенные скобки.

Кроме понятия дерева в литературе часто используется понятие леса. Лес – это множество содержащие несколько непересекающихся деревьев. Для примера, если исключить корневой узел А, то мы получим лес.

Важнейшим подмножеством деревьев являются так называемые бинарные деревья. Бинарное дерево это конечное множество узлов, которое может быть пустым, либо состоять из корня вместе с двумя другими бинарными деревьями. Другими словами каждый его узел может иметь 0, 1,.2 детей (но не более); мы будем различать левых и правых детей.

Решение многих алгоритмических задач приводит к необходимости работать с древовидными структурами, так например, алгоритмический анализ алгебраического выражения y=3ln(x+1) – a/x2 приводит к построению дерева вида:

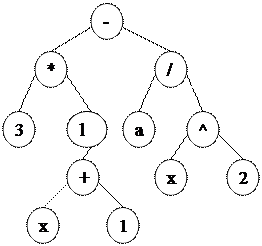
Обход в прямом порядке: посетить корень первого дерева; пройти поддеревья первого дерева; пройти оставшиеся деревья.

- * 3 ln + x 1 / a ^ x 2

Обход в обратном порядке: пройти поддеревья первого дерева; посетить корень первого дерева; пройти оставшиеся деревья. 3 x 1 + ln * a x 2 ^ / -